线性化算法的分类与比较：深入理解不同算法的优缺点

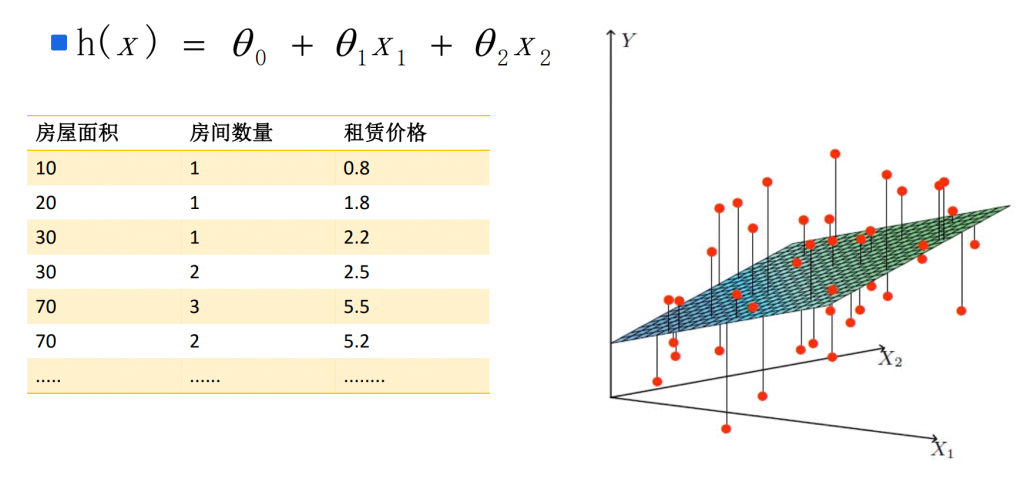
# 1. 线性化算法概述

线性化算法是一种将非线性系统近似为线性系统的技术。非线性系统在实际应用中很常见，但由于其复杂性，难以分析和控制。线性化算法通过将非线性系统在某个工作点附近近似为线性系统，使得非线性系统能够使用线性系统理论进行分析和控制。

线性化算法的原理是利用泰勒级数展开将非线性系统在工作点附近展开为线性系统。泰勒级数展开是一种数学工具，可以将一个函数在某个点附近展开为一个多项式。通过截断泰勒级数展开到一阶或二阶，可以得到非线性系统的线性近似。

# 2. 线性化算法分类

线性化算法可根据其实现方法分为直接线性化算法和间接线性化算法。

### 2.1 直接线性化算法

直接线性化算法直接对非线性模型进行线性化，无需引入中间变量或状态。

#### 2.1.1 逐点线性化

逐点线性化算法在每个操作点对非线性模型进行线性化。具体步骤如下：

- **选择操作点：**选择一个感兴趣的操作点，例如工作点或平衡点。
- **计算雅可比矩阵：**在操作点计算非线性模型的雅可比矩阵，该矩阵包含了模型在该点处的导数信息。
- **线性化：**使用雅可比矩阵在操作点周围对非线性模型进行线性化，得到一个线性模型。

def linearize_jacobian(f, x0):
    """
    逐点线性化算法

    参数：
        f: 非线性函数
        x0: 操作点

    返回：
        线性化后的模型
    """
    J = jacobian(f, x0)  # 计算雅可比矩阵
    return lambda x: J @ (x - x0)  # 线性化模型

#### 2.1.2 拟合线性化

拟合线性化算法通过拟合非线性模型在操作点附近的曲线来获得线性模型。

- **选择操作点：**选择一个感兴趣的操作点。
- **采样数据：**在操作点附近采样非线性模型的输入输出数据。
- **拟合线性模型：**使用采样数据拟合一个线性模型，该模型可以近似非线性模型在操作点附近的行为。

def linearize_fitting(f, x0, n_samples):
    """
    拟合线性化算法

    参数：
        f: 非线性函数
        x0: 操作点
        n_samples: 采样点数

    返回：
        线性化后的模型
    """
    # 采样数据
    X = np.linspace(x0 - 0.1, x0 + 0.1, n_samples)
    Y = f(X)

    # 拟合线性模型
    model = LinearRegression()
    model.fit(X.reshape(-1, 1), Y)

    return model

### 2.2 间接线性化算法

间接线性化算法通过引入中间变量或状态，将非线性模型转换为线性模型。

#### 2.2.1 输入输出线性化

输入输出线性化算法将非线性模型的输入和输出进行线性化。

- **引入虚拟输入：**引入一个虚拟输入，该输入与非线性模型的实际输入相关联。
- **线性化输入：**对虚拟输入进行线性化，得到一个线性输入。
- **线性化输出：**对非线性模型的输出进行线性化，得到一个线性输出。

def linearize_io(f, x0, u0):
    """
    输入输出线性化算法

    参数：
        f: 非线性函数
        x0: 操作点
        u0: 操作点输入

    返回：
        线性化后的模型
    """
    # 引入虚拟输入
    u_virtual = u0 + v

    # 线性化输入
    u_linear = u0 + K_u * v

    # 线性化输出
    y_linear = f(x0, u_linear) + K_y * v

    return y_linear

#### 2.2.2 状态空间线性化

状态空间线性化算法将非线性模型转换为一个状态空间模型，然后对状态空间模型进行线性化。

- **构造状态空间模型：**将非线性模型转换为一个状态空间模型，其中状态变量描述了系统的内部状态。
- **线性化状态空间模型：**对状态空间模型进行线性化，得到一个线性状态空间模型。

def linearize_ss(f, x0, u0):
    """
    状态空间线性化算法

    参数：
        f: 非线性函数
        x0: 操作点
        u0: 操作点输入

    返回：
        线性化后的状态空间模型
    """
    # 构造状态空间模型
    A, B, C, D = ss_model(f, x0, u0)

    # 线性化状态空间模型
    A_linear = A + K_x * v
    B_linear = B + K_u * v

    return A_linear, B_linear, C, D

# 3.1 不同算法的适用范围

不同的线性化算法适用于不同的非线性系统和应用场景。以下是对不同算法适用范围的总结：

| 算法类型 | 适用范围 | 优点 | 缺点 |
|---|---|---|---|
| **逐点线性化** | 非线性系统在特定工作点附近 | 简单易行，计算量小 | 精度受工作点变化影响较大 |
| **拟合线性化** | 非线性系统在一定范围内 | 精度较高，鲁棒性较好 | 计算量较大，需要选择合适的拟合函数 |
| **输入输出线性化** | 非线性系统具有可测量的输入和输出 | 精度较高，鲁棒性较好 | 需要建立准确的输入输出模型 |
| **状态空间线性化** | 非线性系统具有可测量的状态变量 | 精度较高，鲁棒性较好 | 需要建立准确的状态空间模型 |

### 3.2 算法的精度和鲁棒性

算法的精度是指线性化模型与非线性系统实际行为的接近程度。鲁棒性是指线性化模型对非线性系统参数变化的敏感程度。

逐点线性化算法的精度受工作点变化影响较大，鲁棒性较差。拟合线性化算法的精度较高，鲁棒性较好，但需要选择合适的拟合函数。输入输出线性化算法和状态空间线性化算法的精度和鲁棒性都较好，但需要建立准确的模型。

### 3.3 算法的复杂度和计算效率

算法的复杂度是指算法所需的计算量。计算效率是指算法执行所需的时间。

逐点线性化算法的复杂度和计算效率都很低。拟合线性化算法的复杂度和计算效率中等。输入输出线性化算法和状态空间线性化算法的复杂度和计算效率较高，但可以通过优化算法和并行计算等技术来提高。

在选择线性化算法时，需要综合考虑不同算法的适用范围、精度、鲁棒性、复杂度和计算效率等因素，以满足具体的应用需求。

# 4. 线性化算法在实践中的应用

线性化算法在控制系统和信号处理等领域有着广泛的应用。本章将介绍线性化算法在这些领域的具体应用场景，并探讨其优势和局限性。

### 4.1 控制系统中的线性化应用

在控制系统中，线性化算法被用于将非线性系统近似为线性系统，从而简化控制器的设计和分析。

#### 4.1.1 线性化模型的建立

建立线性化模型的过程通常涉及以下步骤：

1. **选择线性化点：**确定系统在特定操作点附近进行线性化的状态。
2. **泰勒展开：**在选定的线性化点处对非线性系统进行泰勒展开，保留到一阶或二阶导数项。
3. **状态空间表示：**将展开后的非线性系统转换为状态空间表示，其中状态变量表示系统的内部状态。

#### 4.1.2 线性化模型的应用

线性化模型在控制系统中的应用包括：

- **控制器设计：**使用线性控制理论设计控制器，如比例-积分-微分 (PID) 控制器或状态反馈控制器。
- **系统分析：**分析线性化模型的稳定性、响应性和鲁棒性，以预测系统的整体行为。
- **仿真：**使用线性化模型进行系统仿真，以评估控制器的性能和系统响应。

### 4.2 信号处理中的线性化应用

在信号处理中，线性化算法被用于将非线性信号转换为线性信号，从而简化后续的信号处理操作。

#### 4.2.1 非线性信号的线性化

非线性信号的线性化可以通过以下方法实现：

- **分段线性化：**将非线性信号划分为多个线性段，并在每个线性段内进行线性化。
- **Volterra级数：**将非线性信号表示为 Volterra 级数，其中每一项都是线性函数。
- **神经网络：**使用神经网络来近似非线性信号的线性化函数。

#### 4.2.2 线性化后的信号处理

线性化后的信号可以进行各种信号处理操作，包括：

- **滤波：**使用线性滤波器去除噪声或增强特定频率分量。
- **特征提取：**提取线性化信号中的特征，用于模式识别或分类。
- **压缩：**使用线性编码技术压缩线性化信号，以减少存储或传输所需的带宽。

### 4.3 优势和局限性

线性化算法在实践中具有以下优势：

- **简化分析和设计：**将非线性系统近似为线性系统，简化了控制系统和信号处理的分析和设计过程。
- **提高精度：**在非线性系统接近线性化点时，线性化模型可以提供较高的精度。
- **计算效率：**线性化模型的计算通常比非线性模型更有效率。

然而，线性化算法也存在一些局限性：

- **精度受限：**线性化模型只能在非线性系统接近线性化点时提供准确的近似。
- **鲁棒性差：**线性化模型对系统参数的变化敏感，可能导致精度下降。
- **适用范围有限：**线性化算法不适用于高度非线性的系统。

# 5. 线性化算法的最新进展

随着科学技术的发展，线性化算法的应用领域不断拓展，研究人员也在不断探索新的线性化方法，以提高线性化算法的精度、鲁棒性和适用性。本章将介绍线性化算法的最新进展，包括基于机器学习的线性化方法、多变量系统的线性化算法和鲁棒线性化算法。

### 5.1 基于机器学习的线性化方法

机器学习技术的发展为线性化算法提供了新的思路。基于机器学习的线性化方法利用机器学习算法从数据中学习非线性系统的线性化模型。这些方法可以有效地解决传统线性化算法难以处理的复杂非线性系统。

**5.1.1 神经网络线性化**

神经网络是一种强大的机器学习算法，可以近似任何非线性函数。神经网络线性化方法利用神经网络来学习非线性系统的输入输出关系，并建立线性化模型。

import tensorflow as tf

# 定义神经网络模型
model = tf.keras.models.Sequential([
  tf.keras.layers.Dense(units=10, activation='relu', input_shape=(n_features,)),
  tf.keras.layers.Dense(units=1)
])

# 训练神经网络
model.compile(optimizer='adam', loss='mean_squared_error')
model.fit(X_train, y_train, epochs=100)

# 使用神经网络进行线性化
y_pred = model.predict(X_test)

**5.1.2 支持向量机线性化**

支持向量机是一种分类和回归算法，可以有效地处理非线性数据。支持向量机线性化方法利用支持向量机来学习非线性系统的输入输出关系，并建立线性化模型。

from sklearn.svm import SVR

# 定义支持向量机模型
model = SVR(kernel='rbf', gamma='auto')

# 训练支持向量机
model.fit(X_train, y_train)

# 使用支持向量机进行线性化
y_pred = model.predict(X_test)

### 5.2 多变量系统的线性化算法

多变量系统是指具有多个输入和多个输出的系统。传统线性化算法通常只适用于单变量系统。多变量系统的线性化算法需要考虑多个输入和输出之间的相互作用。

**5.2.1 多输入多输出线性化**

多输入多输出线性化算法可以将具有多个输入和多个输出的非线性系统线性化为一组线性方程组。

import numpy as np

# 定义多输入多输出线性化算法
def mimo_linearization(f, x0, u0):
  """
  多输入多输出线性化算法

  参数：
    f: 非线性系统函数
    x0: 初始状态
    u0: 初始输入

  返回：
    A: 状态转移矩阵
    B: 输入矩阵
    C: 输出矩阵
    D: 直接透传矩阵
  """

  # 计算雅可比矩阵
  A = np.array([[f(x0 + dx, u0)[0] - f(x0, u0)[0]] / dx for dx in np.eye(len(x0))])
  B = np.array([[f(x0, u0 + du)[0] - f(x0, u0)[0]] / du for du in np.eye(len(u0))])
  C = np.array([[f(x0, u0)[1] - f(x0, u0)[1]] / dx for dx in np.eye(len(x0))])
  D = np.array([[f(x0, u0)[1] - f(x0, u0)[1]] / du for du in np.eye(len(u0))])

  return A, B, C, D

**5.2.2 状态空间多变量线性化**

状态空间多变量线性化算法可以将具有多个输入和多个输出的非线性系统线性化为一组状态方程和输出方程。

import numpy as np

# 定义状态空间多变量线性化算法
def state_space_linearization(f, x0, u0):
  """
  状态空间多变量线性化算法

  参数：
    f: 非线性系统函数
    x0: 初始状态
    u0: 初始输入

  返回：
    A: 状态转移矩阵
    B: 输入矩阵
    C: 输出矩阵
    D: 直接透传矩阵
  """

  # 计算雅可比矩阵
  A = np.array([[f(x0 + dx, u0)[0] - f(x0, u0)[0]] / dx for dx in np.eye(len(x0))])
  B = np.array([[f(x0, u0 + du)[0] - f(x0, u0)[0]] / du for du in np.eye(len(u0))])
  C = np.array([[f(x0, u0)[1] - f(x0, u0)[1]] / dx for dx in np.eye(len(x0))])
  D = np.array([[f(x0, u0)[1] - f(x0, u0)[1]] / du for du in np.eye(len(u0))])

  return A, B, C, D

### 5.3 鲁棒线性化算法

鲁棒线性化算法可以生成对系统参数变化和外部扰动鲁棒的线性化模型。鲁棒线性化算法可以提高线性化模型的精度和可靠性。

**5.3.1 鲁棒逐点线性化**

鲁棒逐点线性化算法利用鲁棒优化技术来生成对系统参数变化和外部扰动鲁棒的逐点线性化模型。

import numpy as np
import cvxpy as cp

# 定义鲁棒逐点线性化算法
def robust_pointwise_linearization(f, x0, u0, delta):
  """
  鲁棒逐点线性化算法

  参数：
    f: 非线性系统函数
    x0: 初始状态
    u0: 初始输入
    delta: 扰动范围

  返回：
    A: 状态转移矩阵
    B: 输入矩阵
    C: 输出矩阵
    D: 直接透传矩阵
  """

  # 定义优化变量
  A = cp.Variable((len(x0), len(x0)))
  B = cp.Variable((len(x0), len(u0)))
  C = cp.Variable((len(x0), len(x0)))
  D = cp.Variable((len(x0), len(u0)))

  # 定义优化目标
  objective = cp.Minimize(cp.norm(f(x0 + delta, u0) - (A @ x0 + B @ u0 + C @ delta + D)))

  # 定义优化约束
  constraints = [
    A @ x0 + B @ u0 + C @ delta + D == f(x0, u0),
    cp.norm(delta) <= delta
  ]

  # 求解优化问题
  prob = cp.Problem(objective, constraints)
  prob.solve()

  return A.value, B.value, C.value, D.value

**5.3.2 鲁棒状态空间线性化**

鲁棒状态空间线性化算法利用鲁棒控制理论来生成对系统参数变化和外部扰动鲁棒的状态空间线性化模型。

import numpy as np
import scipy.linalg as la

# 定义鲁棒状态空间线性化算法
def robust_state_space_linearization(f, x0, u0, delta):
  """
  鲁棒状态空间线性化算法

  参数：
    f: 非线性系统函数
    x0: 初始状态
    u0: 初始输入
    delta: 扰动范围

  返回：
    A: 状态转移矩阵
    B: 输入矩阵
    C: 输出矩阵
    D: 直接透传矩阵
  """

  # 计算雅可比矩阵
  A = np.array([[f(x0 + dx, u0)[0] - f(x0, u0)[0]] / dx for dx in np.eye(len(x0))])
  B = np.array([[f(x0, u0 + du)[0] - f(x0, u0)[0]] / du for du in np.eye(len(u0))])
  C = np.array([[f(x0, u0)[1] - f(x0, u0)[1]] / dx for dx in np.eye(len(x0))])
  D = np.array([[f(x0, u0)[1] - f(x0, u0)[1]] / du for du in np.eye(len(u0))])

  # 计算鲁棒性指标
  gamma = la.norm

# 6. 线性化算法的未来展望

线性化算法在各个领域都有着广泛的应用，随着科学技术的发展，线性化算法也面临着新的挑战和机遇。

### 6.1 复杂系统的线性化

随着科学技术的发展，系统变得越来越复杂，传统的线性化算法难以满足复杂系统的线性化需求。因此，未来研究的重点之一是开发针对复杂系统的线性化算法。

### 6.2 实时线性化

在一些应用场景中，需要对系统进行实时线性化，以适应系统参数的变化。因此，未来研究的另一个重点是开发实时线性化算法，以满足实时控制和信号处理的需求。

### 6.3 鲁棒线性化

在实际应用中，系统参数往往存在不确定性，这会影响线性化模型的精度。因此，未来研究需要重点关注鲁棒线性化算法，以提高线性化模型对参数变化的鲁棒性。

### 6.4 多变量系统的线性化

在许多实际应用中，系统往往是多变量的。传统的线性化算法难以处理多变量系统，因此，未来研究需要重点开发多变量系统的线性化算法。

### 6.5 基于机器学习的线性化

近年来，机器学习技术在各个领域取得了显著进展。机器学习技术可以用来构建线性化模型，并提高线性化模型的精度和鲁棒性。因此，未来研究需要重点探索基于机器学习的线性化算法。