多变量系统辨识秘籍


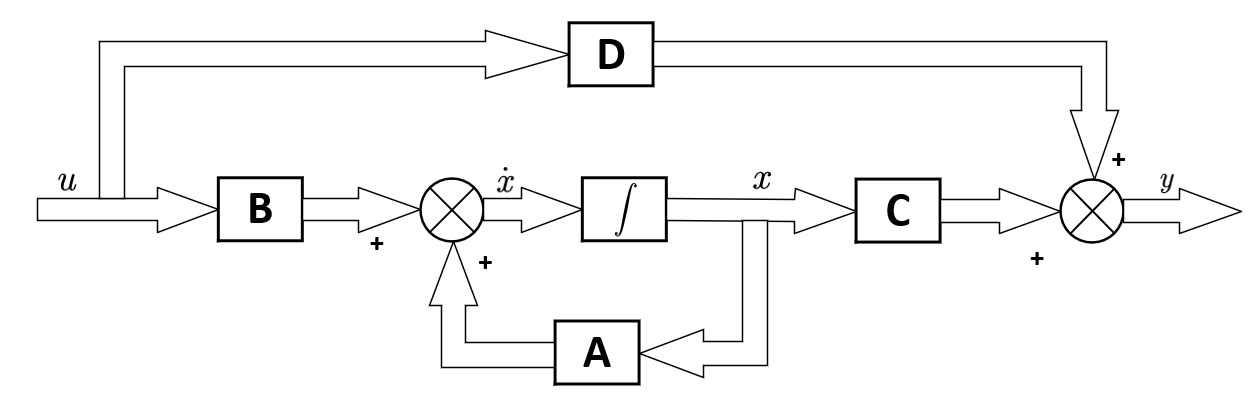
# 摘要
多变量系统辨识是控制工程、信号处理和经济建模等多个领域中一种重要的技术，它涉及从观测数据中提取系统模型的过程。本文首先概述了多变量系统辨识的基本概念和理论基础，然后深入探讨了线性和非线性多变量系统的辨识方法，并介绍了实际中使用的软件工具和平台。通过工业过程控制、经济数据分析和医学信号处理等具体案例，分析了系统辨识的实际应用效果和存在的挑战。最后，本文提出了一些优化策略，并对多变量系统辨识技术的未来发展方向进行了展望。

# 关键字
系统辨识；多变量系统；参数估计；最小二乘法；软件工具；优化策略

参考资源链接：[经典辨识法：SISO线性过程的MATLAB仿真——面积法与Hankel矩阵法](https://wenku.csdn.net/doc/6412b4eabe7fbd1778d4147c?spm=1055.2635.3001.10343)
# 1. 多变量系统辨识概述

在现代工业与科技飞速发展的背景下，系统辨识作为一种通过观测数据建立数学模型的技术，对于多变量复杂系统的分析和预测起到了至关重要的作用。**多变量系统辨识**涉及多个输入和输出变量，这些变量之间存在复杂的相互作用和依赖关系。相较于单变量系统，多变量系统在辨识过程中增加了模型的复杂性和计算量，但同时也提供了更为全面的系统描述，为提高控制精度和决策能力提供了可能。本章将概括介绍多变量系统辨识的基本概念，为后续章节对理论基础、辨识算法实践、案例分析以及优化与挑战的深入探讨打下基础。

# 2. 多变量系统辨识理论基础

### 2.1 系统辨识的基本概念

#### 2.1.1 系统辨识的定义和重要性

系统辨识是控制理论和应用统计学交叉领域中的一个重要分支。它的核心目标是从实际系统的观测数据中，建立一个数学模型来描述系统的动态特性。这种数学模型通常需要反映输入与输出之间的关系，从而可以通过该模型对系统的行为进行预测、控制或优化。

系统辨识之所以重要，在于其能够为缺乏精确数学模型的复杂系统提供可行的建模方法。在工业自动化、经济分析、生物医学工程等多个领域，系统辨识技术都有着广泛的应用。例如，在机器人技术中，通过系统辨识可以准确地建立动力学模型，实现精确控制；在金融分析中，利用历史数据建立股市预测模型，帮助投资者做出更为理性的决策。

#### 2.1.2 系统辨识的主要方法和模型

系统辨识的方法按照模型的类型主要分为两大类：参数模型和非参数模型。参数模型通过确定一组固定的参数来描述系统的特性，而非参数模型则不需要预先设定参数的具体形式。

常见的参数模型包括自回归模型（AR）、移动平均模型（MA）以及自回归移动平均模型（ARMA）。这些模型在时间序列分析中非常普遍。而神经网络模型、模糊逻辑模型以及高斯过程模型等则属于非参数模型。这些模型因其灵活性和通用性而被广泛应用于模式识别、预测等领域。

### 2.2 多变量系统的特点与挑战

#### 2.2.1 多变量系统的定义和特性

多变量系统指的是输入和输出变量个数多于一个的系统。这类系统的典型特点是变量之间存在交叉影响，即输入变量不仅影响对应的输出，还可能影响其他输出。与单变量系统相比，多变量系统的辨识更加复杂，因为需要同时考虑多个输入输出变量间的动态关系。

多变量系统的另一个特性是其控制和分析的复杂性较高。在设计控制策略时，必须考虑系统各个变量之间的耦合效应，这在单变量系统中是不需要的。

#### 2.2.2 多变量系统辨识的难点

多变量系统的辨识难点主要体现在以下几个方面：

1. **耦合性**：多变量系统中的变量往往相互耦合，使得系统模型的建立变得更加困难。
2. **信息量大**：多变量系统需要处理更多的数据，数据处理和存储的要求随之提高。
3. **计算复杂度高**：在进行参数估计和模型验证时，计算量往往随着变量数目的增加呈指数级增长。

### 2.3 参数估计理论

#### 2.3.1 参数估计的原理

参数估计的原理是通过从观测数据中提取信息，估计模型参数，使得模型的预测输出与实际观测数据之间差异最小。在多变量系统辨识中，常见的参数估计方法包括最小二乘法、极大似然法和贝叶斯估计等。

最小二乘法是最基础的参数估计方法，其基本思想是通过最小化观测数据与模型预测之间的误差平方和来确定参数。这种方法在数据线性相关时效果最佳。

极大似然法则是通过优化似然函数（或其对数）来确定模型参数。对于复杂的多变量系统，它往往能够提供更为准确的参数估计。

贝叶斯估计则引入了先验信息，并利用贝叶斯定理来更新参数的后验分布。这种方法在处理不确定性和噪声较大的系统中非常有用。

#### 2.3.2 常用的参数估计方法

下面将具体介绍在多变量系统辨识中常用的几种参数估计方法。

##### 最小二乘法（OLS）

最小二乘法是一种广泛应用于线性模型参数估计的方法。其基本思想是选择模型参数，使得残差平方和最小。具体操作步骤如下：

1. 建立线性模型：`Y = Xβ + ε`，其中`Y`为观测值向量，`X`为已知的输入矩阵，`β`为模型参数向量，`ε`为误差项。
2. 误差平方和定义为：`S(β) = (Y - Xβ)'(Y - Xβ)`。
3. 对`β`求导，并令导数为0，以求得最小化`S(β)`的参数估计值`β̂`。

代码实现：

# 假设 X 和 Y 已经准备好
# X <- ... # 输入矩阵
# Y <- ... # 输出向量

# 使用最小二乘法求解参数 β
beta_hat <- solve(t(X) %*% X) %*% t(X) %*% Y

##### 极大似然估计（MLE）

极大似然估计是一种基于概率分布的参数估计方法。对于给定的数据集，选择参数`θ`使似然函数最大化。具体步骤如下：

1. 假设数据由某个概率模型生成，该模型取决于参数`θ`。
2. 定义似然函数`L(θ) = P(X|θ)`，为观测数据`X`发生时参数`θ`的概率。
3. 通常在实际应用中，我们处理对数似然函数`l(θ) = log(L(θ))`，因为它简化了计算。
4. 对数似然函数最大化，往往通过求导并令导数等于0来实现。

代码实现（使用R语言）：

# 极大似然估计的示例代码（以高斯分布为例）
fit <- mle(
  function(mu, sigma) dnorm(x, mean = mu, sd = sigma, log = TRUE),
  start = list(mu = mean(x), sigma = sd(x)),
  data = list(x = x)
)

##### 贝叶斯估计

贝叶斯估计是一种结合先验知识和观测数据的参数估计方法。与最小二乘法和极大似然估计不同，贝叶斯估计不仅返回一个点估计，而且还能给出参数的概率分布（后验分布）。

其核心是贝叶斯定理：`P(θ|X) = P(X|θ)P(θ)/P(X)`，其中`P(θ|X)`是后验概率，`P(X|θ)`是似然函数，`P(θ)`是参数的先验概率，`P(X)`是边缘似然。

通过选择合适的先验分布并利用观测数据来更新对参数的理解，贝叶斯方法可以在不确定性较高的情况下提供更加灵活的模型参数估计。

代码实现（使用R语言）：

# 假设我们已经有关于参数的先验知识
# 先验参数
prior.mean <- 0
prior.sd <- 1

# 观测数据
data <- rnorm(10, mean = 5, sd = 1)

# 后验分布参数计算
post.mean <- (prior.sd^(-2) * prior.mean + length(data) * mean(data)) / (prior.sd^(-2) + length(data))
post.sd <- sqrt(1 / (prior.sd^(-2) + length(data)))

# 贝叶斯估计结果
posterior <- list(mean = post.mean, sd = post.sd)

以上，我们介绍了系统辨识的基本