【Python算法优化】：如何用Decimal库高效解决复杂数学问题

# 1. Python算法优化与Decimal库概述

## 1.1 Python算法优化的重要性
在现代IT行业中，算法的优化对于提升软件性能和效率至关重要。Python作为一门广泛应用于多个领域的高级编程语言，其算法优化更是受到了广泛关注。由于Python语言的简洁性和易用性，程序员可以快速开发出原型，但在一些计算密集型的任务中，标准数据类型可能会遇到性能瓶颈。

## 1.2 数学计算中的挑战
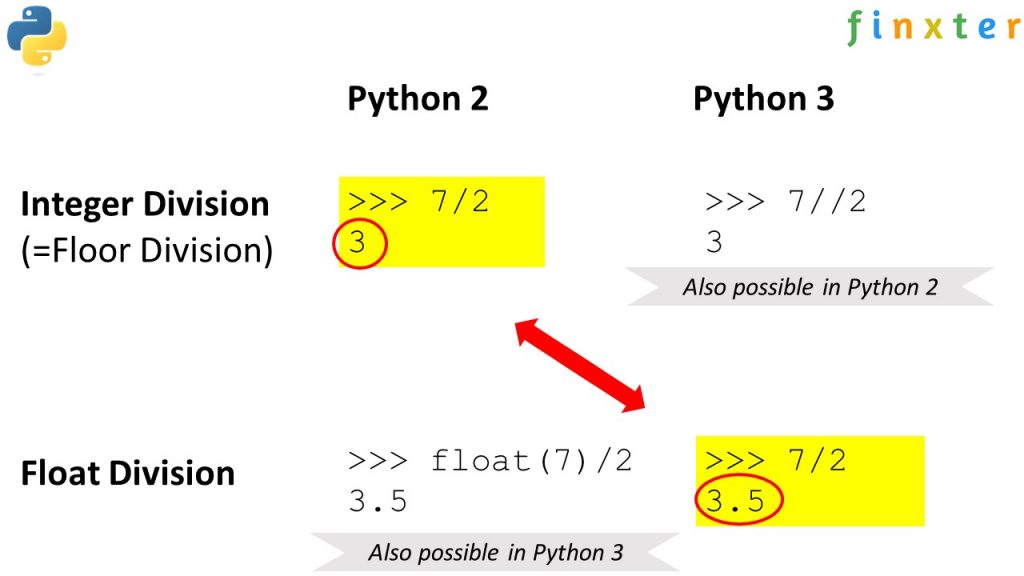
Python中的浮点数由于其内部表示方式的限制，在处理需要高精度计算的问题时会遇到一些挑战。例如，0.1无法在计算机中被精确表示，从而导致一系列精度问题。这些问题在财务计算、科学研究等要求高准确性的领域中尤为突出。

## 1.3 Python Decimal库的引入
为了应对这些挑战，Python提供了Decimal库，它允许我们在任意精度下进行数学计算。Decimal库特别适合处理金融和科学计算中的精确计算需求，它可以避免浮点数运算中的精度问题，从而提高算法的准确性和性能。在接下来的章节中，我们将深入探讨如何使用Decimal库来优化算法，以及它的高级特性和实际应用场景。

# 2. Python中复杂数学问题的挑战

### 2.1 数学计算的精度问题

#### 2.1.1 浮点数的精度误差

在进行数学计算时，浮点数精度误差是Python开发者经常遇到的问题。由于浮点数在计算机内的二进制表示存在限制，这导致了无法精确表示某些十进制数。例如，十进制中的0.1在二进制中是一个无限循环小数，因此在存储时只能取近似值。这样在进行多次运算后，精度误差会累积，影响最终结果。

# 浮点数精度误差的示例
a = 0.1 + 0.1 + 0.1 - 0.3
print(a)  # 输出结果为 5.***e-17，理论上应为0

代码解释：通过简单的浮点数加减操作，可以观察到由于精度问题导致的结果与理论值偏差。

#### 2.1.2 精度误差对算法性能的影响

精度误差不仅会影响数值计算的结果，还可能对算法性能产生影响。在金融、科学计算等领域，不精确的数值可能会导致错误的决策或结论。精度误差还可能引起迭代算法中的震荡或发散，使得算法性能降低，甚至无法收敛到正确的解。

# 精度误差影响算法性能的示例
def calculate_interest(principal, rate, years):
    return principal * (1 + rate / 100) ** years

principal = 1000
rate = 2.5
years = 3
# 使用浮点数计算复利
actual_result = calculate_interest(principal, rate, years)
# 使用Decimal进行精确计算
from decimal import Decimal
decimal_result = calculate_interest(Decimal(principal), Decimal(rate), years)
print(f"浮点数计算结果: {actual_result}")
print(f"Decimal计算结果: {decimal_result}")

参数说明：在这个例子中，我们比较了使用浮点数和Decimal库进行复利计算的结果。使用Decimal可以显著提高计算的精度。

### 2.2 精确计算的需求场景

#### 2.2.1 财务计算的精确性要求

在财务计算中，精确性是至关重要的。例如，货币交易、利息计算、成本估算等，都需要精确到小数点后几位。这些场景中，任何轻微的误差都可能导致公司财务上的损失，甚至法律责任问题。

| 需求场景 | 精确度要求 | 示例 |
|----------|------------|------|
| 货币计算 | 小数点后两位 | 银行账户的交易 |
| 股票交易 | 小数点后四位 | 高频交易的股票价格 |
| 成本预算 | 小数点后三位 | 大型项目的成本预估 |

表格说明：上表列举了几种财务计算场景以及在这些场景中对于数值精度的要求。

#### 2.2.2 科学计算的数据完整性

在科学计算中，数据的完整性和精确性是保障研究准确性的基础。例如，在天文学、物理学和化学等领域，研究者们需要进行复杂的数值模拟和精确的数据分析，以确保实验结果的可靠性。

# 科学计算中的精确性要求示例
import math

# 圆周率的精确表示
pi = Decimal('3.***')
radius = Decimal('10')

# 计算圆面积
area = pi * (radius ** 2)
print(f"精确计算得到的圆面积是: {area}")

代码解释：在科学计算中，使用Decimal库能够保证在复杂公式运算中，中间结果和最终结果的高精确度。

### 2.3 Python内置类型与性能瓶颈

#### 2.3.1 内置数值类型性能分析

Python的内置数值类型（如int和float）在处理日常计算时表现良好，但面对需要高精度的计算时，就会遇到瓶颈。内置类型无法满足某些特定需求，比如在财务计算中，小数点后多位的精确计算是必需的。

flowchart LR
    A[开始] --> B[定义浮点数]
    B --> C[执行计算]
    C --> D{检查精度}
    D -- "精度满足" --> E[继续下一步]
    D -- "精度不足" --> F[寻找替代方案]
    F --> G[使用Decimal]
    G --> H[执行高精度计算]
    H --> I[结束]

流程图说明：该流程图展示了在需要高精度计算时，从内置类型向Decimal库过渡的逻辑。

#### 2.3.2 传统算法性能优化的局限性

使用Python内置类型时，算法性能优化通常依赖于提高算法效率和减少不必要的计算。但这些优化在解决精度问题时有限制，因为它们无法解决由浮点数表示本身导致的精度误差。

# 传统算法优化示例
import timeit

def fast_power(base, exponent):
    result = 1
    for _ in range(exponent):
        result *= base
    return result

# 测试优化前后的时间差异
fast_time = timeit.timeit('fast_power(2, 100)', globals=globals(), number=10000)
print(f"快速幂算法耗时：{fast_time}秒")

代码解释：此示例代码中我们使用快速幂算法替代直接的幂运算来优化性能。但是，即便优化了算法，仍然无法解决浮点数固有的精度限制问题。

# 3. Python的Decimal库详解

Python的Decimal库是专门为高精度数值计算而设计的，它提供了一个Decimal数据类型用于十进制浮点运算。与传统的二进制浮点数不同，Decimal类型是基于十进制的，因此可以进行精确的十进制运算，尤其适用于需要精确小数计算的场合。

## 3.1 Decimal库的数据结构与原理

### 3.1.1 Decimal对象和Context管理

Decimal库中的核心是`Decimal`对象，它能够表示一个精确的十进制数。`Decimal`对象有以下几个关键属性：

- `digits`：表示小数点后有效数字的数量。
- `exponent`：表示小数点的位置。
- `