堆栈在逆转算法中的应用：【高效逆序】，数据结构变魔术

# 1. 堆栈数据结构基础

在本章中，我们将介绍堆栈数据结构的基本概念。堆栈是一种后进先出（LIFO）的数据结构，它的操作限制在仅允许在表的一端进行插入和删除操作。这种特性让堆栈成为解决特定问题的有力工具。

## 1.1 堆栈操作的基本原理

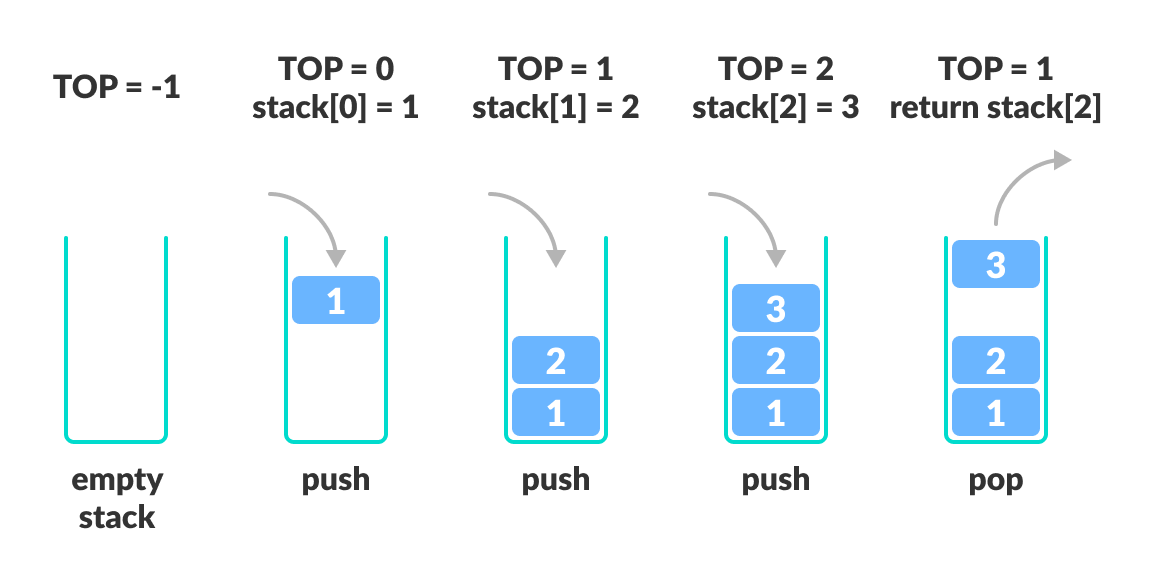
堆栈提供了两种主要操作：入栈（Push）和出栈（Pop）。入栈操作是在堆栈的顶部添加一个元素，而出栈操作是从堆栈顶部移除一个元素。堆栈的这一特性意味着最后被添加的元素将会是第一个被移除的，这与现实生活中的栈原理相似。

## 1.2 堆栈的数据结构特点

堆栈的操作特点决定了其数据结构非常简单。通常只需要一个数组和一个指针来指示栈顶位置。这样的结构使得堆栈的实现和操作都非常高效，这也是其在编程中广泛应用的原因之一。

我们将会在后续章节中深入探讨堆栈的应用和逆转算法的实现，从基础到应用，逐一展开。

# 2. 堆栈的逆转算法实现

## 2.1 堆栈操作的基本原理

堆栈是一种后进先出（LIFO, Last In First Out）的数据结构，它支持两种操作：入栈（Push）和出栈（Pop）。在这一小节中，我们将深入理解这两个核心操作以及堆栈数据结构的特点。

### 2.1.1 入栈（Push）与出栈（Pop）操作

入栈操作是将一个元素添加到堆栈的顶部，即将其放置在当前的栈顶元素之上。出栈操作则是移除堆栈顶部的元素，返回它，并将新的栈顶元素移至原来的位置。

这里是一个简单的入栈操作的代码示例，以及对应的逻辑分析：

def push(stack, item):
    """
    将元素压入堆栈顶部。
    参数:
    stack (list): 一个列表，用作堆栈。
    item: 要压入堆栈的元素。
    """
    stack.append(item)  # 将元素添加到列表末尾，列表末尾相当于堆栈的顶部

# 示例使用
my_stack = []
push(my_stack, 1)
push(my_stack, 2)
print(my_stack)  # 输出: [1, 2]

在上面的代码块中，我们首先定义了一个`push`函数，该函数接受两个参数：`stack`和`item`。`stack`是一个列表，用于模拟堆栈的数据结构；`item`是我们希望压入堆栈的元素。通过调用列表的`append`方法，我们将新元素添加到列表的末尾，模拟入栈操作。

出栈操作的代码示例如下：

def pop(stack):
    """
    从堆栈顶部移除元素，并返回它。
    参数:
    stack (list): 一个列表，用作堆栈。
    返回:
    被移除的元素。
    """
    if not stack:
        return None  # 如果堆栈为空，返回None
    return stack.pop()  # 移除并返回列表最后一个元素，模拟堆栈的出栈操作

# 示例使用
print(pop(my_stack))  # 输出: 2
print(pop(my_stack))  # 输出: 1
print(my_stack)  # 输出: []，堆栈为空

在`pop`函数中，如果堆栈为空（即列表为空），函数返回`None`。否则，它调用列表的`pop`方法来移除并返回列表的最后一个元素，这模拟了堆栈的出栈操作。

### 2.1.2 堆栈的数据结构特点

堆栈作为一个基本数据结构，拥有两个非常重要的特点：后进先出（LIFO）和作用域限制。

- **后进先出（LIFO）**：最后加入堆栈的元素会是第一个被移除的元素。这一特性在程序设计中经常用于保存和恢复变量的状态。
- **作用域限制**：堆栈提供了一个局部的作用域，这使得在复杂的程序中能够控制变量的作用范围，并保证它们的访问是按照特定的顺序进行的。

## 2.2 逆转算法的理论基础

逆转算法是一种在数据结构中重新排列元素顺序的算法，其核心目标是将一个序列中的元素顺序颠倒。在堆栈的逆转算法实现中，我们关注如何利用堆栈的特性来完成这一任务。

### 2.2.1 逆转算法的数学模型

逆转算法可以看作是一个置换问题，数学上可以通过置换函数P来表示，P(n)表示将序列中的第n个元素移动到序列的第1个位置。对于堆栈而言，由于其LIFO的特性，逆序过程可以通过连续的入栈和出栈操作来实现。

### 2.2.2 时间复杂度与空间复杂度分析

逆转算法的时间复杂度通常是指完成整个序列逆转所需要的步骤数。对于堆栈操作而言，如果我们有n个元素需要逆转，每次出栈和入栈算作一个步骤，那么至少需要2n个步骤，因此时间复杂度为O(n)。

空间复杂度则是算法在执行过程中所占用的额外空间量。在逆转算法中，我们只需要一个堆栈来临时存储元素，因此空间复杂度为O(n)，这里的n为堆栈中元素的数量。

## 2.3 实现逆转算法的关键步骤

要实现堆栈的逆转算法，关键步骤包括递归逆转和迭代方法。我们分别介绍这两种方法，并分析它们的特点和优劣。

### 2.3.1 堆栈的递归逆转方法

递归逆转是一种利用递归函数来实现逆转的策略。该方法的核心思想是递归地将堆栈中的元素移动到临时堆栈中，然后再逐个移动回原堆栈，从而实现逆转。

递归逆转的代码示例如下：

def recursive_reverse(stack):
    """
    递归方式逆转堆栈。
    参数:
    stack (list): 一个列表，用作堆栈。
    """
    if len(stack) == 0:
        return stack
    else:
        recursive_reverse(stack)  # 递归处理剩余元素
        stack.append(stack.pop(0))  # 将元素移到临时堆栈，再移回原堆栈完成逆转

# 示例使用
my_stack = [1, 2, 3, 4, 5]
recursive_reverse(my_stack)
print(my_stack)  # 输出: [5, 4, 3, 2, 1]

在这个示例中，我们通过递归调用`recursive_reverse`函数来处理堆栈中的元素。每一次递归调用都会取出堆栈的第一个元素，并将其放置在堆栈的底部。这个过程一直持续到堆栈为空为止。

### 2.3.2 迭代方法与算法优化

迭代方法则使用循环结构来实现堆栈的逆转。相比于递归方法，迭代方法通常更为高效，因为它避免了函数调用的开销，并且不受到递归调用栈深度的限制。

迭代逆转的代码示例如下：

def iterative_reverse(stack):
    """
    迭代方式逆转堆栈。
    参数:
    stack (list): 一个列表，用作堆栈。
    """
    while stack:
        stack.append(stack.pop(0))  # 将元素从底部移除并立即放回顶部，完成逆转
    return stack

# 示例使用
my_stack = [1, 2, 3, 4, 5]
iterative_reverse(my_stack)
print(my_stack)  # 输出: [5, 4, 3, 2, 1]

在迭代逆转中，我们使用一个`while`循环来重复出栈和入栈操作，直到堆栈为空。每次循环中，我们从堆栈的底部取出元素，并将其放回顶部。这种方法的时间复杂度为O(n)，空间复杂度同样为O(n)。

通过递归和迭代方法的对比，我们可以发现递归逆转更简洁但可能因为递归调用消耗大量内存，而迭代逆转虽然在逻辑上稍复杂，却更加高效且稳定。

在下一章节中，我们将介绍堆栈在不同类型数据逆转中的应用，这将涵盖数组、链表以及字符串数据的逆转过程，并通过实际编码实例进行详细解释。

# 3. 堆栈在不同类型数据逆转中的应用

堆栈作为数据结构中的基本元素，在处理逆转任务时展示出其独特的魅力和高效性。本章将深入探讨堆栈在不同数据类型逆转过程中的具体应用，包括数组、链表和字符串数据的逆转，并展示相关的编程实例，深入分析其应用的内涵。

## 3.1 数组数据的逆转

### 3.1.1 基于堆栈的数组逆转步骤

数组的逆转操作是指将数组中的元素顺序颠倒，例如将`[1, 2, 3, 4, 5]`变为`[5, 4, 3, 2, 1]`。利用堆栈的后进先出（LIFO）特性，可以轻松实现数组的逆转。以下是基于堆栈实现数组逆转的基本步骤：

1. 初始化一个空堆栈。
2. 从数组开始到结束遍历每个元素，并依次将它们压入堆栈中。
3. 同时，创建一个新的数组，用于存放逆转后的元素。
4. 每次将一个元素压入堆栈后，再将其弹出，并将弹出的元素存放到新数组的相应位置。
5. 当所有