【避免统计陷阱】：正确认识置信区间与概率的区别

# 1. 统计学的基本概念

统计学是研究数据收集、分析、解释和呈现的科学。它不仅仅关注数字本身，更多的是从数字中提取有意义的信息，帮助我们理解世界并做出基于数据的决策。在统计学中，我们经常讨论的两个核心概念是“参数”和“统计量”。

## 参数与统计量的定义
参数通常指的是描述整个总体特性的量，它们是固定的，但往往未知。例如，总体平均数、总体标准差等。统计量则是从样本中计算出来的，用来估计总体参数，例如样本平均数、样本方差等。

## 统计推断的基石
统计推断建立在样本与总体的关系之上。通过样本数据我们可以推断总体的特性，但推断的准确性依赖于样本的代表性。统计推断包括点估计和区间估计，其中置信区间是区间估计中非常重要的一个概念，将在后续章节详细探讨。

通过理解统计学的基本概念，我们可以为更深入地探讨统计推断、置信区间、概率论以及在实际中的应用奠定基础。而随着数据在决策过程中的重要性日益增加，掌握这些知识对于IT行业人员同样至关重要。

# 2. 置信区间理论与计算

### 2.1 置信区间的定义与重要性

#### 2.1.1 置信区间的统计学定义
置信区间是统计学中一个核心概念，它给出了一个范围，我们相信这个范围内包含了总体参数的真实值。具体来说，如果我们从一个总体中反复抽取大小为n的样本，并计算每个样本的置信区间，那么在100(1-α)%的置信水平下，大约有100(1-α)%的置信区间会包含这个总体参数的真实值。

这种概念在实践中非常有用，因为一般情况下我们无法直接测量总体参数，而只能通过样本信息来推断。置信区间提供了一个合理的估计范围，让研究者能够对总体参数进行更为精确的推断。

#### 2.1.2 置信区间与总体参数的关系
置信区间与总体参数之间存在着一种内在的统计关系。总体参数，如总体均值或总体比例，是我们希望知道但通常无法直接获得的信息。通过构建置信区间，我们可以评估我们的样本估计与总体参数之间的一致性。

置信区间的宽度受到多种因素的影响，包括样本大小、总体标准差和置信水平。较大的样本量、较小的标准差或者较高的置信水平都会导致置信区间变宽，反之则变窄。但是，过窄的置信区间可能会增加错误地将样本统计量作为总体参数的风险，而过宽的置信区间又可能缺乏足够的信息价值。因此，找到恰当的平衡点至关重要。

### 2.2 置信区间的计算方法

#### 2.2.1 样本均值与标准误差
计算置信区间的基础之一是样本均值，它是总体均值的一个估计量。样本均值本身是一个随机变量，会围绕总体均值上下波动。标准误差是样本均值的标准差，反映了这种波动的大小。公式如下：

标准误差(SE) = \frac{\sigma}{\sqrt{n}}

其中，σ是总体标准差，n是样本大小。

#### 2.2.2 不同置信水平下的计算案例
当计算置信区间时，置信水平的选择也非常重要。通常，研究者会选择95%或者99%的置信水平，这取决于对置信区间精确度的需求。以下是一个95%置信区间的计算案例：

假定我们从一个正态分布的总体中随机抽取一个样本，总体标准差σ未知，样本大小为n。计算95%置信区间的方法如下：

\bar{x} \pm Z_{\alpha/2} \times SE

其中，\(\bar{x}\)是样本均值，\(Z_{\alpha/2}\)是对应于所选置信水平的Z分数，在95%置信水平下，\(Z_{\alpha/2}\)约等于1.96。SE是样本均值的标准误差。

表2-1展示了不同置信水平下的Z分数：

| 置信水平 | Z分数 |
|-------------|--------|
| 90% | 1.645 |
| 95% | 1.96 |
| 99% | 2.576 |

### 2.3 置信区间在实际应用中的考虑

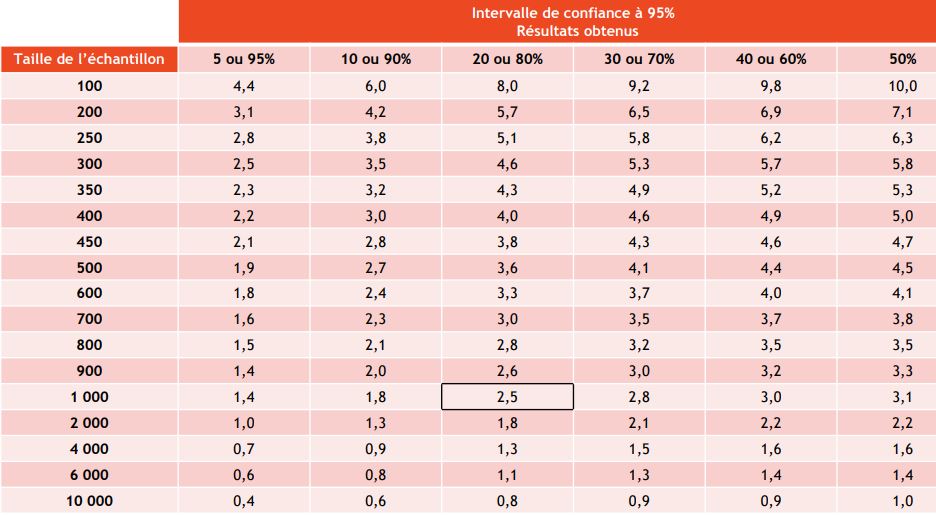
#### 2.3.1 样本量大小的影响
样本量的大小直接影响置信区间的宽度。样本量越大，标准误差越小，置信区间越窄，表示我们对总体参数的估计就越精确。使用公式：

SE = \frac{S}{\sqrt{n}}

其中，S是样本标准差。因此，增加样本量能够提高置信区间的精确度。

#### 2.3.2 异常值处理与置信区间
异常值可能会显著影响样本均值和标准误差，进而影响置信区间的准确度。在处理异常值时，应考虑其出现的原因。如果异常值是由于测量误差或输入错误造成的，则应予以纠正或删除。如果异常值是合理数据，则应保留，但需要对置信区间进行调整。

在R语言中，可以使用箱线图识别异常值，示例代码如下：

# 生成一组包含异常值的数据
data <- c(rnorm(100), 1000)

# 绘制箱线图
boxplot(data)

通过上述章节，我们可以看到置信区间理论及其计算方法的细致入微的分析，接下来我们将探讨概率基础及其与置信区间的关联。

# 3. 概率基础及其与置信区间的关联

概率论是统计学中的核心部分，它为我们提供了理解和计算置信区间所必需的基本工具和方法。概率论的许多原则和概念是构建置信区间的基石，理解这些基础概念对于正确使用置信区间至关重要。

## 3.1 概率论的基本原则

概率论的基本原则是理解置信区间理论的前提条件。它不仅帮助我们量化不确定性，而且是推断统计学的理论基础。我们将从随机事件和概率的基本概念开始，然后逐步深入探讨条件概率以及独立性。

### 3.1.1 随机事件与概率

在统计学和概率论中，随机事件是指在一定条件下可能发生也可能不发生的现象。对于这些随机事件，我们通常关心它们发生的概率。

**概率的定义**：概率是衡量某个事件发生的可能性的数值。如果事件 A 在实验中发生，则事件 A 的概率 P(A) 介于 0 和 1 之间（0 ≤ P(A) ≤ 1）。如果 P(A) = 0，表示事件 A 在实验中不可能发生；如果 P(A) = 1，表示事件 A 在实验中必定发生。

**概率的计算**：对于有限个结果的随机实验，每个结果发生的概率可以通过将特定结果的发生次数除以总结果次数来计算。对于一些特殊的情况，例如掷硬币或掷骰子，我们可以直接使用经典概率的计算方法。

**代码示例**：