深入理解MATLAB矩阵连接与合并：揭秘矩阵连接和合并的原理与应用

# 1. MATLAB矩阵连接与合并概述

矩阵连接和合并是MATLAB中用于组合和操作数据的两个基本操作。它们在数据分析、图像处理、机器学习等广泛的应用中发挥着至关重要的作用。

**矩阵连接**将两个或多个矩阵水平或垂直连接在一起，从而创建具有更多行或列的新矩阵。它用于合并来自不同来源或具有不同形状的数据集。

**矩阵合并**将两个或多个矩阵沿特定维度（行或列）连接在一起，从而创建具有相同形状的新矩阵。它用于组合具有相同结构但不同内容的数据集。

# 2. 矩阵连接的理论基础

### 2.1 矩阵连接的概念和类型

矩阵连接是指将两个或多个矩阵按照一定规则组合成一个新的矩阵。在MATLAB中，矩阵连接主要有两种类型：水平连接和垂直连接。

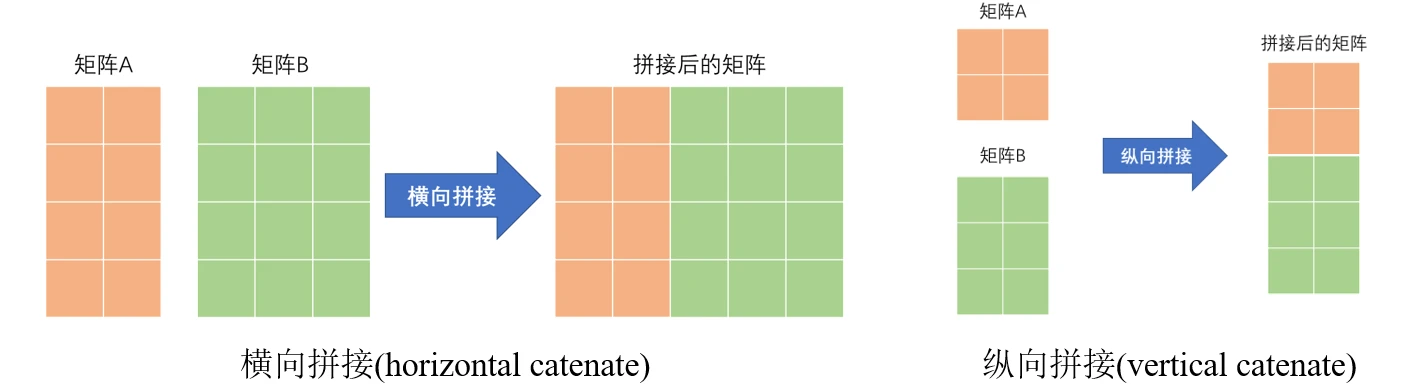
**水平连接（cat(2, A, B, ...))**：将多个矩阵按列连接在一起，形成一个新的矩阵。其中，A、B等为待连接的矩阵。

**垂直连接（cat(1, A, B, ...))**：将多个矩阵按行连接在一起，形成一个新的矩阵。其中，A、B等为待连接的矩阵。

### 2.2 矩阵连接的数学原理

矩阵连接的数学原理基于线性代数中的矩阵运算。水平连接对应于矩阵的列拼接，垂直连接对应于矩阵的行拼接。

**水平连接（列拼接）**：

[A B] = [a11 a12 ... a1n | b11 b12 ... b1m]
[A2 B2] = [a21 a22 ... a2n | b21 b22 ... b2m]
[An Bn] = [an1 an2 ... ann | bn1 bn2 ... bnm]

**垂直连接（行拼接）**：

[A; B] = [a11 a12 ... a1n]
         [a21 a22 ... a2n]
         ...
         [an1 an2 ... ann]
         [b11 b12 ... b1m]
         [b21 b22 ... b2m]
         ...
         [bn1 bn2 ... bnm]

### 2.3 矩阵连接的MATLAB实现

MATLAB提供了`cat`函数用于实现矩阵连接。`cat`函数的语法如下：

C = cat(dim, A, B, ...)

其中：

* `C`：输出的连接矩阵
* `dim`：连接维度，1表示垂直连接，2表示水平连接
* `A`、`B`等：待连接的矩阵

#### 代码示例

**水平连接（列拼接）**：

A = [1 2 3; 4 5 6];
B = [7 8 9; 10 11 12];
C = cat(2, A, B);

disp(C)

输出：

1     2     3     7     8     9
4     5     6    10    11    12

**垂直连接（行拼接）**：

A = [1 2 3; 4 5 6];
B = [7 8 9; 10 11 12];
C = cat(1, A, B);

disp(C)

输出：

1     2     3
4     5     6
7     8     9
10    11    12

# 3.1 矩阵合并的概念和类型

矩阵合并是指将多个矩阵沿特定维度组合成一个新矩阵的过程。与矩阵连接不同，矩阵合并将多个矩阵组合成一个单一的实体，而不是创建新的矩阵。

矩阵合并的类型取决于要合并的矩阵的维度和形状。最常见的矩阵合并类型包括：

- **水平合并（行合并）：**将多个矩阵沿行方向合并，形成一个具有更多列的新矩阵。
- **垂直合并（列合并）：**将多个矩阵沿列方向合并，形成一个具有更多行的新矩阵。
- **深度合并：**将多个三维或更高维度的矩阵沿深度方向合并，形成一个具有更大深度的三维或更高维度的矩阵。

### 3.1.1 水平合并（行合并）

水平合并（行合并）使用 `[A, B, C, ...]` 语法，其中 `A`、`B`、`C` 等是需要合并的矩阵。合并后的矩阵具有与输入矩阵相同的行数，但列数是所有输入矩阵列数的总和。

% 创建三个矩阵
A = [1, 2, 3; 4, 5, 6];
B = [7, 8, 9; 10, 11, 12];
C = [13, 14, 15; 16, 17, 18];

% 水平合并矩阵
D = [A, B, C];

% 打印合并后的矩阵
disp(D)

1     2     3     7     8     9    13    14    15
4     5     6    10    11    12    16    17    18

### 3.1.2 垂直合并（列合并）

垂直合并（列合并）使用 `[A; B; C; ...]` 语法，其中 `A`、`B`、`C` 等是需要合并的矩阵。合并后的矩阵具有与输入矩阵相同的列数，但行数是所有输入矩阵行数的总和。

% 创建三个矩阵
A = [1, 2, 3; 4, 5, 6];
B = [7, 8, 9; 10, 11, 12];
C = [13, 14, 15; 16, 17,