揭秘MATLAB矩阵机器学习应用：深入理解矩阵在机器学习中的关键作用

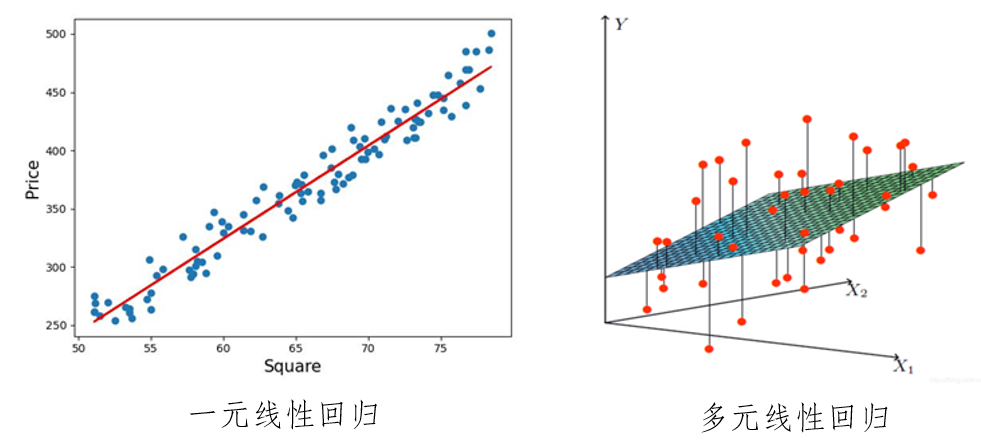
# 1. MATLAB矩阵简介

MATLAB矩阵是一种用于存储和操作数字数据的强大数据结构。它由按行和列组织的元素组成，形成一个二维数组。矩阵在机器学习中扮演着至关重要的角色，因为它提供了表示和处理复杂数据集的有效方式。

MATLAB矩阵具有丰富的功能，包括：

- **元素访问和操作：**使用索引和切片访问和修改矩阵中的元素。
- **矩阵运算：**执行加法、减法、乘法和除法等基本矩阵运算。
- **矩阵函数：**应用各种函数，如求逆、特征值和特征向量，以分析和操作矩阵。
- **矩阵可视化：**使用图像和热图等工具可视化矩阵，以获得数据的直观表示。

# 2. 矩阵在机器学习中的应用理论

### 2.1 矩阵的线性代数基础

#### 2.1.1 矩阵的运算和性质

**矩阵的运算**

矩阵的运算包括加法、减法、数乘和矩阵乘法。

* **加法和减法：**两个同阶矩阵可以进行加法或减法，对应元素相加或相减。
* **数乘：**一个矩阵可以与一个标量相乘，每个元素都乘以该标量。
* **矩阵乘法：**两个矩阵可以相乘，结果矩阵的元素是第一个矩阵的行向量与第二个矩阵的列向量的内积。

**矩阵的性质**

* **对角矩阵：**主对角线以外元素都为 0 的矩阵。
* **单位矩阵：**主对角线元素都为 1，其他元素都为 0 的矩阵。
* **对称矩阵：**转置等于自身的矩阵。
* **正交矩阵：**转置等于其逆矩阵。

#### 2.1.2 矩阵的特征值和特征向量

**特征值和特征向量**

矩阵的特征值是使矩阵与单位矩阵相减后，乘以特征向量仍等于特征向量的标量。特征向量是对应于该特征值的非零向量。

**求解特征值和特征向量**

求解矩阵的特征值和特征向量可以通过求解特征方程：

(A - λI)x = 0

其中：

* A 是给定的矩阵
* λ 是特征值
* I 是单位矩阵
* x 是特征向量

**代码块：**

% 给定矩阵 A
A = [2 1; 3 4];

% 求解特征值和特征向量
[V, D] = eig(A);

% 特征值
eigenvalues = diag(D);

% 特征向量
eigenvectors = V;

**逻辑分析：**

* `eig` 函数求解矩阵的特征值和特征向量，返回特征值矩阵 `D` 和特征向量矩阵 `V`。
* `diag(D)` 提取 `D` 的对角元素，得到特征值。
* `V` 的列向量是特征向量。

### 2.2 矩阵在机器学习中的数学原理

#### 2.2.1 矩阵分解与降维

**矩阵分解**

矩阵分解将一个矩阵分解为多个较小的矩阵，可以简化计算并提取有用的信息。常见的矩阵分解包括：

* **奇异值分解（SVD）：**将矩阵分解为奇异值、左奇异向量和右奇异向量的乘积。
* **主成分分析（PCA）：**将矩阵分解为特征向量和特征值的乘积，用于降维。

**降维**

降维是将高维数据投影到低维空间，减少计算量和提高可解释性。矩阵分解可以用于降维，例如：

* **PCA：**通过投影数据到主成分轴，将高维数据降维到低维空间。

#### 2.2.2 矩阵优化与正则化

**矩阵优化**

矩阵优化是指寻找使目标函数最小的矩阵。常见的矩阵优化方法包括：

* **梯度下降：**迭代地更新矩阵以减小目标函数。
* **共轭梯度法：**一种更快的梯度下降方法，利用共轭方向。

**正则化**

正则化是一种技术，通过添加惩罚项来防止过拟合。常见的正则化方法包括：

* **L1 正则化：**惩罚矩阵元素的绝对值和。
* **L2 正则化：**惩罚矩阵元素的平方和。

# 3. 矩阵在机器学习中的实践应用

### 3.1 矩阵在分类问题中的应用

#### 3.1.1 逻辑回归中的矩阵应用

逻辑回归是一种广为使用的分类算法，它使用矩阵来表示数据和模型参数。

**数据表示：**

逻辑回归将输入数据表示为一个特征矩阵 `X`，其中每一行表示一个数据点，每一列表示一个特征。

**模型参数：**

逻辑回归模型的参数是一个权重向量 `w`，它决定了每个特征对分类结果的影响。

**分类过程：**

逻辑回归使用 sigmoid 函数将特征矩阵 `X` 和权重向量 `w` 相乘的结果转换为概率值。概率值表示数据点属于某一类的可能性。

# 逻辑回归模型
import numpy as np
from sklearn.linear_model import LogisticRegression

# 数据准备
X = np.array([[1, 2], [3, 4], [5, 6]])
y = np.array([0, 1, 1])

# 模型训练
model = LogisticRegression()
model.fit(X, y)

# 预测
predictions = model.predict(X)

**参数说明：**

* `X`：特征矩阵，形状为 (n_samples, n_features)
* `y`：标签向量，形状为 (n_samples,)
* `model`：训练好的逻辑回归模型
* `predictions`：预测结果，形状为 (n_samples,)

#### 3.1.2 支持向量机中的矩阵应用

支持向量机 (SVM) 是一种强大的分类算法，它使用矩阵来表示数据和模型参数。

**数据表示：**

SVM 将输入数据表示为一个特征矩阵 `X`，其中每一行表示一个数据点，每一列表示一个特征。

**模型参数：**

SVM 模型的参数包括支持向量 `sv` 和决策边界 `b`。支持向量是位于决策边界上的数据点，而决策边界是一个超平面，将数据点分为不同的类。

**分类过程：**

SVM 使用核函数将特征矩阵 `X` 转换为一个高维空间，并在该空间中找到决策边界。决策边界将数据点分为不同的类。

# 支持向量机模型
import numpy as np
from sklearn.svm import SVC

# 数据准备
X = np.array([[1, 2], [3, 4], [5, 6]])
y = np.array([0, 1, 1])

# 模型训练
model = SVC()
model.fit(X, y)

# 预测
predictions = model.predict(X)

**参数说明：**

* `X`：特征矩阵，形状为 (n_samples, n_features)
* `y`：标签向量，形状为 (n_samples,)
* `model`：训练好的 SVM 模型
* `predictions`：预测结果，形状为 (n_samples,)

### 3.2 矩阵在聚类问题中的应用

#### 3.2.1 K均值聚类中的矩阵应用

K均值聚类是一种流行的聚类算法，它使用矩阵来表示数据和聚类中心。

**数据表示：**

K均值聚类将输入数据表示为一个数据矩阵 `X`，其中每一行表示一个数据点，每一列表示一个特征。

**聚类中心：**

K均值聚类算法选择 `k` 个聚类中心，它们是数据点在特征空间中的代表点。

**聚类过程：**

K均值聚类算法迭代地将数据点分配到最近的聚类中心，并更新聚类中心的位置