基数排序深度分析：大数据量排序的秘密武器

# 1. 基数排序基础概述

基数排序（Radix Sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于其不依赖于元素之间的比较，适用于整数排序，尤其在整数具有固定位数时表现出色。基数排序可以扩展到字符串排序，并且在数据范围受到限制时可以达到线性时间复杂度，因此在某些特定应用场景下具有极高的效率。

与其他排序算法相比，基数排序不需要额外的内存空间进行元素交换，而是利用数组下标的原地排序。这种排序方式在处理大量数据时，可以降低内存的消耗，同时，在数据量大且数据分布均匀时，具有较高的效率。然而，基数排序也有其局限性，例如当数据的位数差异很大时，其性能可能不如一些比较型排序算法。

在接下来的章节中，我们将深入探讨基数排序的理论基础，并通过实际案例演示其实践应用。同时，我们也会关注在大数据场景下基数排序的表现，以及如何优化该算法以适应不同需求的场景。

# 2. 基数排序的理论基础

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。其核心思想是分治，将大问题分解为小问题分别解决。本章将深入探讨基数排序的理论基础，包括排序算法的种类与比较、工作原理、与其它排序算法的对比，以及稳定性与复杂度分析。

## 2.1 排序算法概述

### 2.1.1 排序算法的种类与比较

排序算法是计算机科学中一个非常基础且广泛讨论的主题。常见的排序算法包括冒泡排序、选择排序、插入排序、归并排序、快速排序、堆排序、希尔排序、计数排序、桶排序和基数排序等。每种排序算法都有其特定的应用场景、时间复杂度和空间复杂度。

- **冒泡排序**：通过重复遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。冒泡排序对n个项目需要O(n^2)的比较次数，且可以就地排序。尽管这个算法是最简单了解和实现的，但它对于包含大量的元素的数列来说效率很低。
- **快速排序**：通过选取一个“基准”元素，把数列分为两部分，一部分比基准值小，另一部分比基准值大，然后递归地排序两个子序列。快速排序平均时间复杂度为O(nlogn)，最坏情况下为O(n^2)，但通常情况下比其它O(nlogn)算法要快。

- **计数排序、桶排序和基数排序**：特别适用于一定范围内的整数排序。基数排序是通过逐位比较来进行排序的算法，它不比较元素之间的大小，而是根据元素的位值来进行排序。由于其非比较的性质，基数排序可以达到线性时间复杂度，特别适合于大量数据的排序。

### 2.1.2 排序算法的时间复杂度分析

时间复杂度是评估排序算法效率的一个重要指标。对于不同的排序算法，我们可以根据最坏情况、平均情况和最好情况来分析其时间复杂度。

- **最坏情况**：对于冒泡排序和选择排序，其最坏情况时间复杂度均为O(n^2)；快速排序在最坏情况下也是O(n^2)，但是快速排序的平均性能通常优于冒泡排序和选择排序。
- **平均情况**：快速排序、归并排序和堆排序具有O(nlogn)的平均时间复杂度，其中快速排序通常最快。计数排序、桶排序和基数排序具有O(n+k)的时间复杂度（k是数列中整数的最大值）。

- **最好情况**：对于需要大量比较的排序算法，如冒泡排序和选择排序，最好情况的时间复杂度也是O(n^2)，因为这些算法无论如何都要进行比较。对于像快速排序和归并排序这样的分治算法，最好情况的时间复杂度是O(nlogn)。而计数排序、桶排序和基数排序则可以在最理想情况下达到O(n)的时间复杂度。

## 2.2 基数排序的原理

### 2.2.1 基数排序的工作原理

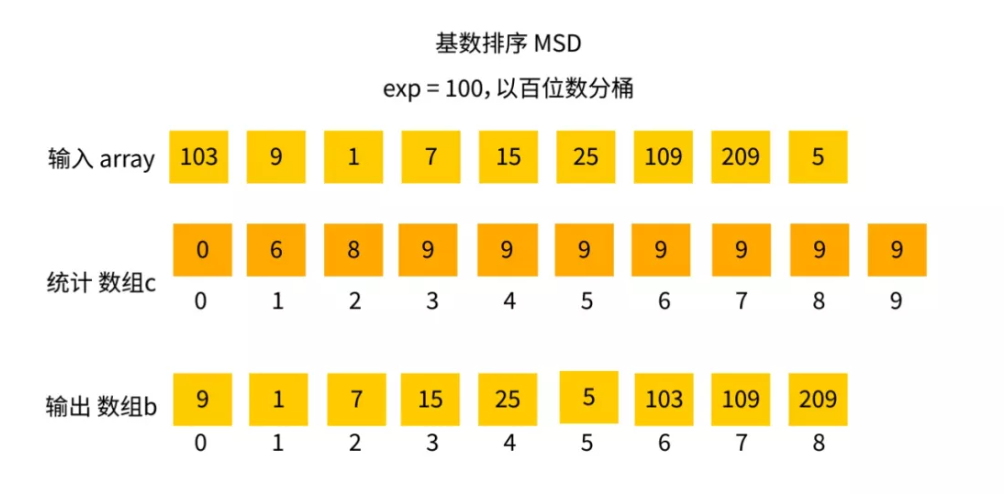
基数排序的流程主要包括两个阶段：首先是“分配”过程，将键值按个位数分配到对应桶中；其次是“收集”过程，按顺序将桶中的值收回到原数组中。然后是十位数、百位数……直到最高位数。

基数排序是一种非比较型的排序算法，它通过整数的位来排序，其时间复杂度为 O(nk)，其中 n 是数组中的元素个数，k 是数字的最大位数。基数排序是通过“分配”和“收集”的方式来对数字进行排序的，但与计数排序不同的是，它不使用整个数组来计数。

该算法的步骤如下：

1. 从个位开始，对数组中每个元素的该位进行排序。这一步可以使用计数排序来实现，因为每个元素的这一位（0-9）的范围是确定的。
2. 完成个位数的排序后，接着对十位数进行排序，然后再是百位数，依此类推，直到最高位。
3. 最后一个桶的元素被收集后，数组就完全有序。

### 2.2.2 基数排序与其他排序算法的对比

基数排序与传统比较型排序算法相比，具有其独特的优缺点。与快速排序相比，基数排序在处理大规模数据集时，尤其当数字范围不大时，通常能够提供更好的性能。然而，当数字范围很大时，基数排序可能不如快速排序高效。

与非比较型排序算法如计数排序或桶排序相比，基数排序可以处理更大范围内的整数，但它需要处理多个桶，这在内存使用和算法实现上更为复杂。计数排序通常用于较小的、有限的整数范围内，其时间复杂度是O(n+k)，k是整数的范围大小。而基数排序则适用于范围较大的整数。

## 2.3 稳定性与复杂度分析

### 2.3.1 基数排序的稳定性探讨

在排序算法中，“稳定性”是指相等的元素在排序之后的相对顺序保持不变。基数排序是一种稳定的排序算法。它通过按位的顺序进行排序，而不会改变具有相同键值的元素之间的相对顺序。这意味着基数排序对于有多个排序标准的复杂数据结构特别有用，因为它能够维持这些标准中的原有顺序。

### 2.3.2 时间复杂度与空间复杂度详析

基数排序的时间复杂度主要取决于数据的位数和数字的范围。对于有d位的n个n进制数的数组，基数排序的时间复杂度为O(d*(n+b))，其中b是用于存储每一位数字的桶的数量。当b是常量时，时间复杂度可以简化为O(d*n)。在实际应用中，当n远大于d时，基数排序的时间复杂度近似于线性时间。

空间复杂度方面，基数排序需要额外的存储空间来存储桶，即为每个可能的键值分配一个桶。对于n个元素和d位数字，基数排序的空间复杂度为O(n+d)。大多数情况下，特别是数字的位数d远小于n时，空间复杂度可以看作是O(n)。

综上所述，基数排序在时间复杂度和空间复杂度方面都有较好的表现，特别是当处理具有较大范围但位数不多的整数时。然而，对于大量数据的排序，尤其是位数很多的数字，实现细节和优化方法将对算法的效率产生显著影响。

在本章节的分析中，我们详细探讨了基数排序的理论基础，包括排序算法的种类、工作原理、稳定性以及时间与空间复杂度。这些理论基础为我们深入理解基数排序提供了坚实的知识支撑，并为下一章实践应用奠定了基础。

# 3. 基数排序的实践应用

基数排序是一种非比较型整数排序算法，通过将整数按位数切割成不同的数字，然后按每个位数分别比较。本章节深入探讨基数排序的实现步骤，以及在实际应用中可能采用的优化策略。

## 3.1 基数排序的实现步骤

### 3.1.1 算法的初始化设置

首先，我们需要对输入数据进行分析，确定需要进行多少轮排序。这取决于输