【高级排序算法特训】：快速排序变种的全方位解读

# 1. 排序算法概述与快速排序简介

## 1.1 排序算法的重要性
排序是计算机科学中的基础问题之一，无论是在数据库、搜索引擎还是日常的数据处理中都扮演着核心角色。它决定了数据的组织方式，影响着数据检索的效率。一个高效的排序算法能够极大地提升处理大规模数据集时的性能。

## 1.2 快速排序的起源
快速排序（Quick Sort）由C. A. R. Hoare在1960年提出，是一种高效的排序算法。它的基本思想是通过一个划分操作将待排序的数组分为两个子数组，其中一个子数组的所有元素都比另一个子数组的元素小，然后再递归地对这两个子数组进行快速排序。

## 1.3 快速排序的适用性
快速排序以其平均时间复杂度为O(n log n)被广泛采用，尤其在平均情况下表现良好。它也适用于大数据集，但当数据接近有序或完全有序时，快速排序的性能会降低。不过，通过一些优化技巧，可以克服这些问题，使得快速排序即使在最坏情况下也能保持较高的效率。

graph TD
    A[排序算法概述] --> B[快速排序简介]
    B --> C[快速排序适用场景]
    C --> D[大数据集排序]
    D --> E[优化策略]
    E --> F[现代编程语言应用]
    F --> G[性能测试与案例研究]

请注意，上述内容仅为第一章的内容示例，它提供了快速排序算法的背景和重要性，并为后续章节的内容打下基础。在实际编写文章时，每个章节都应该具有更加丰富和详细的内容。

# 2. 快速排序的理论基础

快速排序是计算机科学中一个非常重要的算法，也是理解和学习其他排序算法的基础。它由C. A. R. Hoare在1960年提出，以其实现的高效率而闻名。快速排序使用分治法策略，通过一个轴点（pivot）将数组分为两部分，使得一部分的所有元素都比轴点小，而另一部分的所有元素都比轴点大，然后递归地对这两部分继续进行排序。

## 2.1 快速排序原理

### 2.1.1 分治法策略

分治法是一种递归策略，其核心思想是将原问题分解为若干个规模较小但类似于原问题的子问题，递归解决这些子问题，然后再合并其结果以解决原问题。快速排序就是分治法策略的一个典型应用。

快速排序的过程可以总结为三个步骤：

1. **选择轴点（Pivot Selection）**：从数组中选择一个元素作为轴点，通常选择第一个元素、最后一个元素、中间元素或者随机元素。
2. **分区（Partitioning）**：重新排列数组，所有比轴点小的元素摆放在轴点前面，而所有比轴点大的元素摆放在轴点后面。在这个分区退出之后，该轴点就处于数列的中间位置。
3. **递归排序子数组（Recursive Sorting）**：递归地将小于轴点值的子数组和大于轴点值的子数组排序。

### 2.1.2 快速排序过程

下面通过一个示例演示快速排序的整个过程：

假设有一个待排序的数组 `arr = [5, 3, 8, 4, 2, 7, 1, 6]`，我们选择第一个元素 `5` 作为轴点。

1. 分区过程开始：从数组两端交替遍历，小于 `5` 的元素移动到左边，大于 `5` 的元素移动到右边。
分区后得到 `[3, 4, 2, 1]` 在 `5` 的左侧，`[8, 7, 6]` 在 `5` 的右侧。

2. 然后对 `5` 左边的子数组 `[3, 4, 2, 1]` 和右边的子数组 `[8, 7, 6]` 分别进行排序。

3. 递归进行，直到所有子数组的大小为 1，此时数组完全有序。

## 2.2 快速排序的性能分析

### 2.2.1 时间复杂度分析

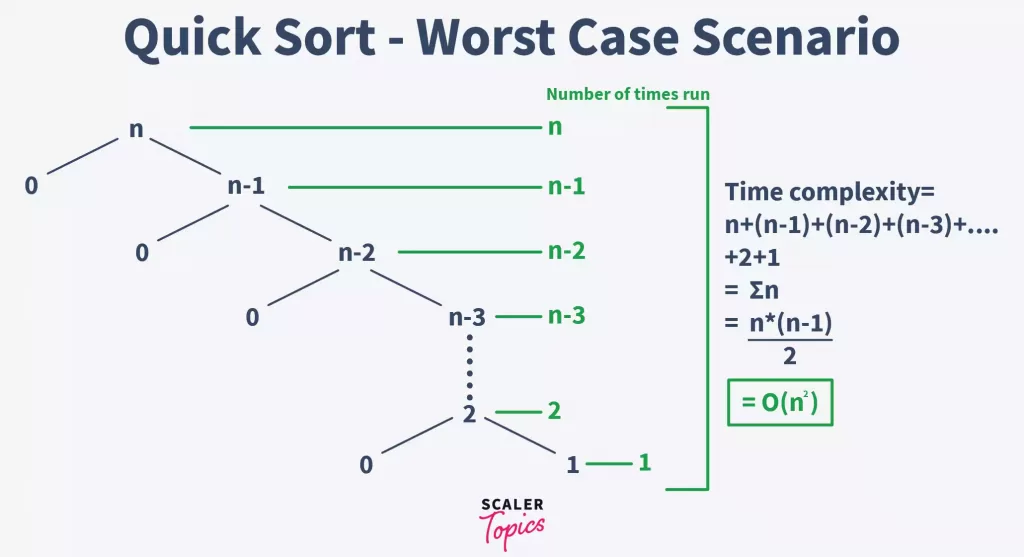
快速排序的平均时间复杂度为 `O(n log n)`，最坏情况下的时间复杂度为 `O(n^2)`。其性能取决于轴点的选择和数组的初始排列。在最好情况下（每次都能完美地分割数组），时间复杂度为 `O(n log n)`，因为每次分割都会将数组分成几乎相等的两部分。然而，在最坏的情况下（每次分割都将数组分成一个元素和其余元素），时间复杂度将退化为 `O(n^2)`。

### 2.2.2 空间复杂度分析

快速排序的空间复杂度为 `O(log n)`，这是因为它需要递归调用栈。在最佳情况下，递归栈的大小为 `O(log n)`；在最差情况下，递归栈的大小为 `O(n)`。尽管快速排序在平均情况下非常高效，但在处理具有大量重复元素的大型数组时，递归栈可能会消耗较多内存。

在下一章，我们会探讨快速排序的常见变种，以及如何通过变种来改善最坏情况下的性能和优化空间复杂度。

# 3. 快速排序的常见变种

快速排序作为一种高效的排序算法，拥有许多改进的版本，以适应不同的使用场景和数据特性。在本章节中，我们将深入探讨快速排序的常见变种，包括双边循环快速排序、三数取中法和非递归快速排序。每个变种都试图在特定条件下提升算法的性能，以适应大数据量的处理。

## 3.1 双边循环快速排序

### 3.1.1 基本思想

双边循环快速排序是对传统快速排序的改进，它将数组分为三部分：小于枢轴、等于枢轴和大于枢轴的元素。这种策略减少了不必要的比较次数，并且更好地处理了元素值重复的情况。双边循环快速排序利用两个索引，从数组的两端向中间遍历，通过交换的方式进行排序，这种方法可以更高效地处理具有大量重