OpenCV多目标模板匹配算法选择指南：匹配算法的优缺点大比拼

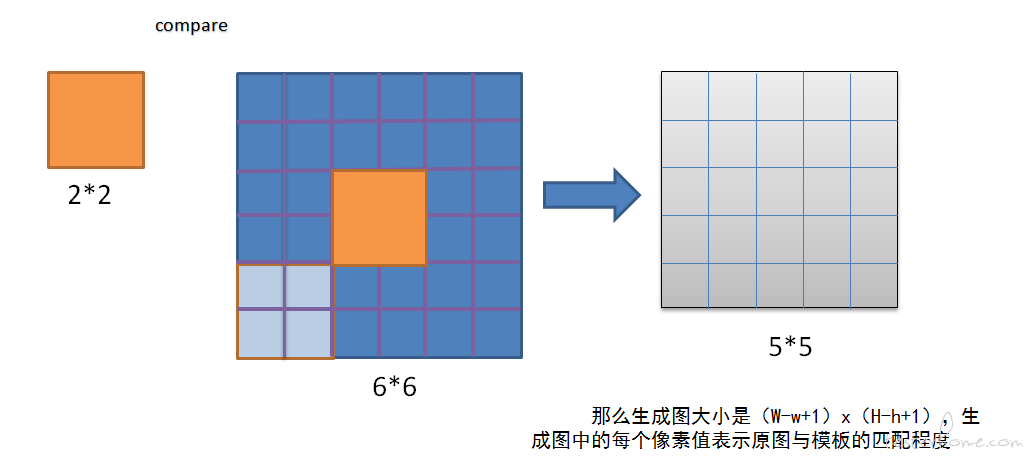
# 1. OpenCV多目标模板匹配概述**

OpenCV中的模板匹配是一种计算机视觉技术，用于在图像中查找与给定模板图像相似的区域。它在目标检测、图像配准和视觉跟踪等应用中得到了广泛应用。

多目标模板匹配扩展了传统模板匹配，允许在图像中同时查找多个目标。这对于识别复杂场景中的多个对象或跟踪移动目标特别有用。OpenCV提供了多种多目标模板匹配算法，每种算法都有自己的优势和劣势，可根据特定应用场景进行选择。

# 2. 基于相关性的模板匹配算法

### 2.1 归一化相关系数 (NCC)

#### 2.1.1 理论基础

归一化相关系数 (NCC) 是一种基于相关性的模板匹配算法，它通过计算模板图像和目标图像之间的相关系数来衡量相似度。相关系数衡量两个变量之间的线性相关程度，范围从 -1 到 1。

NCC 公式如下：

NCC(T, I) = (T - T_mean) * (I - I_mean) / (sqrt(T - T_mean)^2 * sqrt(I - I_mean)^2)

其中：

* T 为模板图像
* I 为目标图像
* T_mean 为模板图像的均值
* I_mean 为目标图像的均值

#### 2.1.2 实践应用

NCC 算法在以下情况下表现良好：

* 图像具有良好的对比度和清晰度
* 模板图像和目标图像大小相似
* 图像中没有显著的噪声或失真

### 2.2 相关系数 (CC)

#### 2.2.1 理论基础

相关系数 (CC) 是 NCC 的简化版本，它不进行归一化操作。CC 公式如下：

CC(T, I) = (T * I) / (sqrt(T^2) * sqrt(I^2))

#### 2.2.2 实践应用

CC 算法与 NCC 算法类似，但它对噪声和失真更敏感。CC 算法适用于以下情况：

* 图像对比度较低或有噪声
* 模板图像和目标图像大小差异较大
* 图像中存在失真或变形

**表格 2.1：NCC 和 CC 算法的比较**

| 特征 | NCC | CC |
|---|---|---|
| 归一化 | 是 | 否 |
| 噪声敏感性 | 低 | 高 |
| 失真敏感性 | 低 | 高 |
| 适用场景 | 对比度高、清晰度高 | 对比度低、有噪声 |

# 3. 基于距离的模板匹配算法

### 3.1 平均绝对差 (SAD)

#### 3.1.1 理论基础

平均绝对差 (SAD) 是一种基于距离的模板匹配算法，它计算模板图像和目标图像之间像素绝对差的平均值。数学公式如下：

SAD(x, y) = (1 / (W * H)) * ∑∑ |T(u, v) - I(u + x, v + y)|

其中：

* `T(u, v)` 是模板图像的像素值
* `I(u + x, v + y)` 是目标图像中与模板图像对齐的像素值
* `W` 和 `H` 分别是模板图像的宽度和高度

#### 3.1.2 实践应用

SAD 算法在实践中具有以下优点：

* 计算简单，速度快
* 对噪声和光照变化具有鲁棒性

但是，SAD 算法也存在以下缺点：

* 对模板图像的旋转和缩放不敏感
* 容易受到极端值的影响

### 3.2 均方根差 (SSD)

#### 3.2.1 理论基础

均方根差 (SSD) 是一种基于距离的模板匹配算法，它计算模板图像和目标图像之间像素平方差的均方根。数学公式如下：

SSD(x, y) = sqrt((1 / (W * H)) * ∑∑ (T(u, v) - I(u + x, v + y))^2)

其中：

* `T(u, v)` 是模板图像的像素值
* `I(u + x, v + y)` 是目标图像中与模板图像对齐的像素值
* `W` 和 `H` 分别是模板图像的宽度和高度

#### 3.2.2 实践应用

SSD 算法在实践中具有以下优点：

* 比 SAD 算法更准确，对模板图像的旋转和缩放更敏感
* 对噪声和光照变化具有鲁棒性

但是，SSD 算法也存在以下缺点：

* 计算量比 SAD 算法更大
* 容易受到极端值的影响

### 比较 SAD 和 SSD 算法

SAD 和 SSD 算法都是基于距离的模板匹配算法，但它们在准确性和计算复杂度方面存在差异。SAD 算法计算简单，速度快，但对模板图像的旋转和缩放不敏感。SSD 算法比 SAD 算法更准确，对模板图像的旋转和缩放更敏感，但计算量更大。

在实际应用中，选择 SAD 或 SSD 算法取决于具体需求。如果需要快速且鲁棒的算法，则 SAD 算法是一