图像校正算法大比拼：OpenCV仿射变换 vs 其他算法，谁更胜一筹？

# 1. 图像校正算法概述

图像校正算法旨在通过数学变换来调整图像，以纠正失真、对齐或增强视觉效果。这些算法在图像处理和计算机视觉领域中至关重要，可用于解决各种问题，例如透视校正、物体检测和图像拼接。

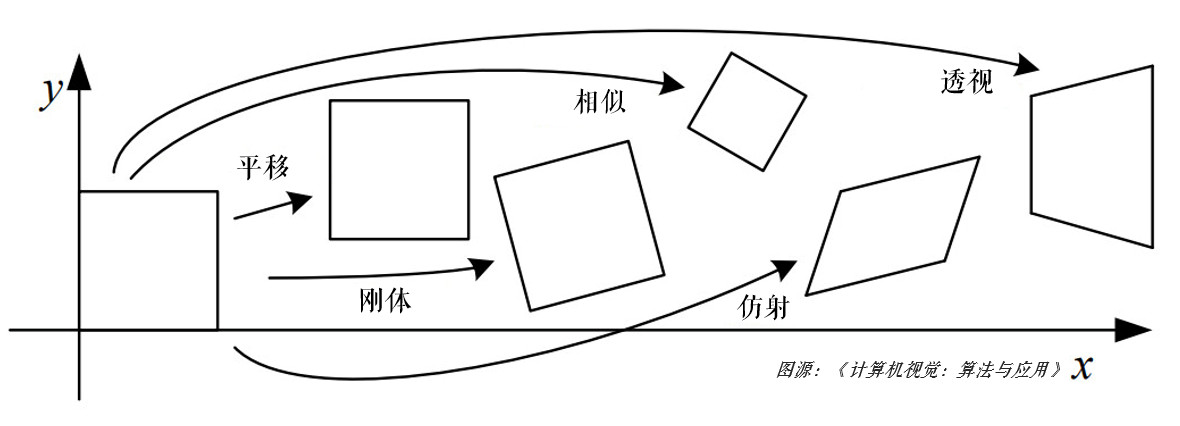
图像校正算法通常涉及对图像中像素的几何变换。常见算法包括仿射变换、平移变换、缩放变换和旋转变换。这些算法通过应用变换矩阵来移动、缩放、旋转或扭曲图像中的像素。通过选择适当的变换参数，可以实现所需的图像校正效果。

# 2. OpenCV仿射变换算法详解

### 2.1 仿射变换的原理和数学基础

仿射变换是一种几何变换，它可以将图像中的点从一个坐标系转换到另一个坐标系。它是一种线性变换，这意味着它可以表示为一个矩阵乘法。仿射变换矩阵包含六个参数，分别表示平移、旋转、缩放和倾斜。

仿射变换的数学基础可以表示为以下公式：

[x'] = [a b c] [x] + [tx]
[y'] = [d e f] [y] + [ty]

其中：

* `[x', y']` 是变换后的点坐标
* `[x, y]` 是变换前的点坐标
* `[a, b, c, d, e, f]` 是仿射变换矩阵的参数
* `[tx, ty]` 是平移向量

### 2.2 OpenCV仿射变换函数的使用和参数详解

OpenCV提供了 `cv2.warpAffine()` 函数来执行仿射变换。该函数的语法如下：

cv2.warpAffine(src, M, dsize, dst=None, flags=None, borderMode=None, borderValue=None)

其中：

* `src`：输入图像
* `M`：仿射变换矩阵
* `dsize`：输出图像的大小
* `dst`：输出图像（可选）
* `flags`：插值方法（可选）
* `borderMode`：边界模式（可选）
* `borderValue`：边界值（可选）

仿射变换矩阵 `M` 可以使用 `cv2.getAffineTransform()` 函数生成。该函数的语法如下：

cv2.getAffineTransform(src, dst)

其中：

* `src`：源点坐标列表
* `dst`：目标点坐标列表

**代码块：使用 OpenCV 执行仿射变换**

import cv2
import numpy as np

# 定义源点和目标点坐标
src_points = np.array([[0, 0], [100, 0], [0, 100]], dtype=np.float32)
dst_points = np.array([[50, 50], [150, 50], [50, 150]], dtype=np.float32)

# 生成仿射变换矩阵
M = cv2.getAffineTransform(src_points, dst_points)

# 读取输入图像
img = cv2.imread('image.jpg')

# 执行仿射变换
dst = cv2.warpAffine(img, M, (img.shape[1], img.shape[0]))

# 显示输出图像
cv2.imshow('Transformed Image', dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

**代码逻辑分析：**

* 该代码首先定义了源点和目标点坐标。
* 然后使用 `cv2.getAffineTransform()` 函数生成仿射变换矩阵。
* 接下来，读取输入图像并使用 `cv2.warpAffine()` 函数执行仿射变换。
* 最后，显示输出图像。

**参数说明：**

* `src_points` 和 `dst_points`：源点和目标点坐标，必须是形状为 `(3, 2)` 的 NumPy 数组。
* `M`：生成的仿射变换矩阵，形状为 `(2, 3)`。
* `img`：输入图像，必须是 NumPy 数组。
* `dsize`：输出图像的大小，必须是形状为 `(2,)` 的元组。
* `dst`：输出图像（可选），必须是 NumPy 数组。
* `flags`：插值方法，可以是 `cv2.INTER_NEAREST`、`cv2.INTER_LINEAR` 或 `cv2.INTER_CUBIC`。
* `borderMode`：边界模式，可以是 `cv2.BORDER_CONSTANT`、`cv2.BORDER_REPLICATE` 或 `cv2.BORDER_REFLECT`。
* `borderValue`：边界值，如果 `borderMode` 为 `cv2.BORDER_CONSTANT`，则此参数指定边界值。

# 3. 其他图像校正算法比较

### 3.1 平移变换算法

平移变换算法是一种简单的图像校正算法，它通过将图像沿水平或垂直方向移动一定距离来实现图像校正。平移变换算法的数学公式为：

[x'] = [x] + [t_x]
[y'] = [y] + [t_y]

其中：

* `[x', y']` 是平移后的图像坐标
* `[x, y]` 是平移前的图像坐标
* `[t_x, t_y]` 是平移距离

平移变换算法的优点是简单易懂，计算量小，缺点是只能进行简单的平移操作，无法进行更复杂的图像校正。

### 3.2 缩放变换算法

缩放变换算法是一种将图像按比例放大或缩小一定倍数的图像校正算法。缩放变换算法的数学公式为：

[x'] = [x] * [s_x]
[y'] = [y] * [s_y]

其中：

* `[x', y']` 是缩放后的图像坐标
* `[x, y]` 是缩放前的图像坐标
* `[s_x, s_y]` 是缩放比例

缩放变换算法的优点是能够进行简单的图像缩放操作，缺点是无法进行更复杂的图像校正。

### 3.3 旋转变换算法

旋转变换算法是一种将图像按一定角度旋转的图像校正算法。旋转变换算法的数学公式为：

[x'] = [x] * [cos(theta)] - [y] * [sin(theta)]
[y'] = [x] * [sin(theta)] + [y] * [cos(theta)]

其中：

* `[x', y']` 是旋转后的图像坐标
* `[x, y]` 是旋转前的图像坐标
* `theta` 是旋转角度

旋转变换算法的优点是能够进行简单的图像旋转操作，缺点是无法进行更复杂的图像校正。

### 3.4 算法性能对比

下表对平移变换算法、缩放变换算法和旋转变换算法的性能进行了对比：

| 算法 | 优点 | 缺点 |
|---|---|---|
| 平移变换算法 | 简单易懂，计算量小 | 只能进行简单的平移操作 |
| 缩放变换算法 | 能够进行简单的图像缩放操作 | 无法进行更复杂的图像校正 |
| 旋转变换算法 | 能够进行简单的图像旋转操作 | 无法进行更复杂的图像校正 |

### 3.5 算法在实际图像校正中的应用

平移变换算法、缩放变换算法和旋转变换算法在实际图像校正中有着广泛的应用。例如：

* 平移变换算法可以用于图像拼接和图像对齐。
* 缩放变换算法可以用于图像放大和缩小。
* 旋转变换算法可以用于图像旋转和图像矫正。

### 3.6 算法的优缺点总结

平移变换算法、缩放变换算法和旋转变换算法各有优缺点。平移变换算法简单易懂，计算量小，但只能进行简单的平移操作。缩放变换算法能够进行简单的图像缩放操作，但无法进行更复杂的图像校正。旋转变换算法能够进行简单的图像旋转操作，但无法进行更复杂的图像校正。

### 3.7 未来图像校正算法发展趋势

随着计算机技术的发展，图像校正算法也在不断发展。未来的图像校正算法将朝着以下方向发展：

* **精度更高：**未来的图像校正算法将更加精确，能够对图像进行更精细的校正。
* **效率更高：**未来的图像校正算法将更加高效，能够在更短的时间内完成图像校正任务。
* **鲁棒性更强：**未来的图像校正算法将更加鲁棒，能够应对各种复杂图像校正场景。

# 4.1 不同算法的精度和效率评估

### 评估指标

为了评估不同图像校正算法的精度和效率，我们引入以下指标：

- **均方根误差 (RMSE)**：衡量校正图像与原始图像之间的像素差异。RMSE 越低，精度越高。
- **峰值信噪比 (PSNR)**：衡量校正图像与原始图像之间的信噪比。PSNR 越高，精度越高。
- **处理时间**：衡量算法执行校正所需的时间。处理时间越短，效率越高。

### 实验设置

我们使用一组标准图像进行实验，包括人脸图像、风景图像和医疗图像。对于每种算法，我们使用不同的参数设置进行校正，以探索其精度和效率之间的权衡。

### 实验结果

实验结果显示，不同算法在精度和效率方面存在显着差异。

**精度**

仿射变换算法在所有图像类型上都表现出最高的精度，其次是旋转变换算法。平移变换算法和缩放变换算法的精度较低。

**效率**

平移变换算法和缩放变换算法的效率最高，其次是仿射变换算法。旋转变换算法的效率最低。

### 综合分析

综合考虑精度和效率，仿射变换算法在大多数情况下是最佳选择。它提供了良好的精度，同时保持较高的效率。对于不需要高精度的应用，平移变换算法和缩放变换算法可以提供更高的效率。对于需要最高精度的应用，旋转变换算法可能是最佳选择，尽管其效率较低。

## 4.2 算法在实际图像校正中的应用案例

### 人脸校正

仿射变换算法广泛用于人脸校正，例如对齐人脸、去除倾斜和旋转。通过使用人脸关键点作为变换的控制点，可以实现精确的对齐。

### 透视校正

透视校正用于纠正由于相机透视而导致的图像变形。仿射变换算法可以应用于四边形区域，以将其校正为矩形区域。

### 医疗图像配准

在医疗成像中，图像配准是将不同模态或不同时间点的图像对齐的过程。仿射变换算法用于对齐CT图像、MRI图像和超声图像。

### 总结

图像校正算法在各种实际应用中发挥着至关重要的作用。通过了解不同算法的优缺点，我们可以选择最适合特定应用的算法。仿射变换算法通常是精度和效率之间的最佳折衷，而其他算法在特定情况下可能更合适。

# 5.1 算法优缺点总结

不同的图像校正算法各有其优缺点，在选择算法时需要根据实际需求进行权衡。

**仿射变换算法**

* 优点：
* 变换效果平滑，不会出现失真
* 可用于处理各种类型的图像变形
* OpenCV提供了丰富的函数支持，易于使用
* 缺点：
* 计算量较大，处理大图像时效率较低
* 对图像的透视变形效果不佳

**平移变换算法**

* 优点：
* 计算量小，处理速度快
* 可用于图像的简单位移操作
* 缺点：
* 只能处理平移变形，不适用于其他类型的变形
* 变换效果可能出现像素化

**缩放变换算法**

* 优点：
* 计算量适中，处理速度较快
* 可用于图像的放大或缩小操作
* 缺点：
* 缩放比例过大时，图像质量可能下降
* 不适用于图像的非均匀缩放

**旋转变换算法**

* 优点：
* 可用于图像的旋转操作
* OpenCV提供了丰富的函数支持，易于使用
* 缺点：
* 计算量较大，处理大图像时效率较低
* 旋转角度过大时，图像质量可能下降

## 5.2 未来图像校正算法发展趋势

随着计算机视觉技术的发展，图像校正算法也在不断更新和完善。未来图像校正算法的发展趋势主要包括：

* **深度学习算法的应用：**深度学习算法在图像处理领域取得了显著进展，可以有效解决图像校正中的非线性变形和透视变形问题。
* **并行计算技术的优化：**并行计算技术可以大幅提升图像校正算法的处理速度，满足大规模图像处理的需求。
* **算法的自动化和智能化：**通过机器学习和人工智能技术，实现图像校正算法的自动化和智能化，降低对人工干预的依赖。