OpenCV仿射变换图像校正常见误区：避免图像校正过程中的陷阱，让图像校正更轻松

# 1. OpenCV仿射变换图像校正简介**

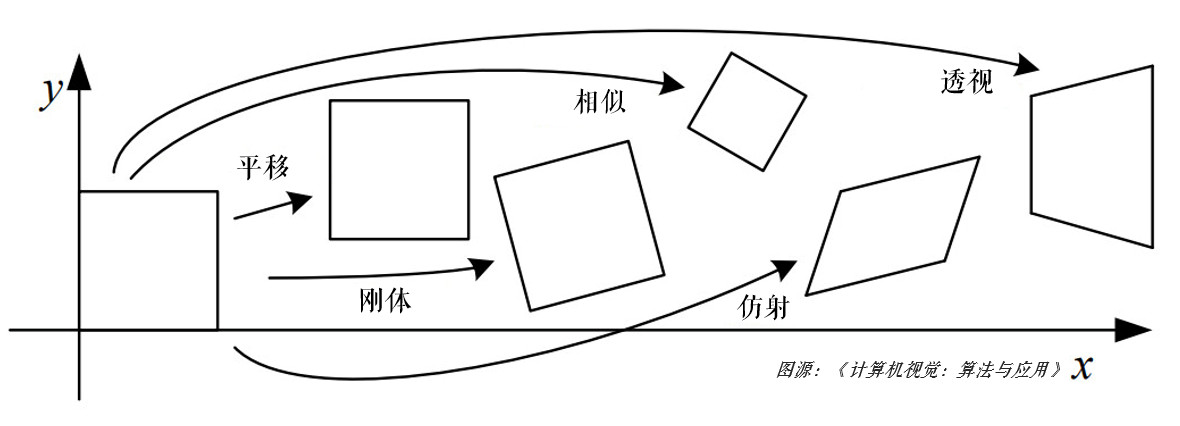
仿射变换是一种图像校正技术，它通过应用一个2x3的变换矩阵来对图像进行平移、旋转、缩放和倾斜等操作。在OpenCV中，仿射变换可以通过warpAffine()函数实现。

仿射变换在图像处理中有着广泛的应用，例如透视校正、旋转校正和缩放校正。通过调整变换矩阵中的参数，我们可以实现各种图像校正效果。在后续章节中，我们将深入探讨仿射变换的理论基础、OpenCV中的实现以及图像校正中的常见误区和最佳实践。

# 2.1 仿射变换的定义和数学原理

仿射变换是一种几何变换，它可以将一个平面上的点集映射到另一个平面上。它是一种线性变换，这意味着它保留了点之间的直线性和平行性。仿射变换可以表示为以下矩阵形式：

[x'] = [a b tx] [x]
[y']   [c d ty] [y]
[1]    [0 0 1]  [1]

其中：

* `[x, y]` 是原始点坐标
* `[x', y']` 是变换后的点坐标
* `[a, b, tx]` 和 `[c, d, ty]` 是仿射变换矩阵的参数

仿射变换矩阵中的参数具有以下含义：

* `a` 和 `c`：缩放因子，沿 x 轴和 y 轴的缩放比例
* `b` 和 `d`：剪切因子，沿 x 轴和 y 轴的剪切角度
* `tx` 和 `ty`：平移因子，沿 x 轴和 y 轴的平移距离

**数学原理**

仿射变换的数学原理基于线性代数。它将原始点坐标 `[x, y]` 乘以仿射变换矩阵，得到变换后的点坐标 `[x', y']`。矩阵乘法的每个元素对应于原始点坐标和变换参数之间的线性组合。

例如，变换后的 x 坐标 `x'` 可以表示为：

x' = a * x + b * y + tx

类似地，变换后的 y 坐标 `y'` 可以表示为：

y' = c * x + d * y + ty

这些方程说明了仿射变换如何通过缩放、剪切和平移来改变点的位置。

# 3. OpenCV中仿射变换的实现

### 3.1 warpAffine()函数的语法和参数

OpenCV中用于进行仿射变换的函数是`warpAffine()`。其语法如下：

cv::warpAffine(
    InputArray src,
    OutputArray dst,
    InputArray M,
    Size dsize,
    int flags = INTER_LINEAR,
    int borderMode = BORDER_CONSTANT,
    const Scalar& borderValue = Scalar()
)

其中，参数的含义如下：

- `src`：输入图像
- `dst`：输出图像
- `M`：仿射变换矩阵
- `dsize`：输出图像的大小
- `flags`：插值方法，默认为线性插值
- `borderMode`：边界处理模式，默认为常量边界
- `borderValue`：边界填充值，仅在`borderMode`为`BORDER_CONSTANT`时有效

### 3.2 仿射变换矩阵的计算方法

仿射变换矩阵是一个3x3的矩阵，其形式如下：

| a b tx |
| c d ty |
| 0 0 1  |

其中，`a`, `b`, `c`, `d`, `tx`, `ty`为仿射变换的参数。

在OpenCV中，可以通过`getAffineTransform()`函数计算仿射变换矩阵。该函数的语法如下