聚类效果优化秘籍：k-means算法提升客户分群质量


# 摘要
K-means算法作为一种广泛应用于数据挖掘领域的聚类算法，在理解和掌握其理论基础的前提下，对于提高数据处理效率及优化业务决策具有重要的实践价值。本文全面介绍了K-means算法的基础知识、应用场景、实际操作过程中的问题解决方法和性能优化策略。重点探讨了算法在客户分群中的应用，详细描述了从数据准备、算法实现到业务价值转化的完整流程。此外，本文还对K-means算法的高级应用进行了深入分析，并通过案例研究展示了其在不同行业中的实际成效。最后，文章展望了大数据环境下K-means算法的发展趋势和未来应用前景，为该领域研究提供了理论和实践的新视角。

# 关键字
K-means算法；聚类分析；数据挖掘；客户分群；性能优化；大数据

参考资源链接：[ARM处理器的LDMIA指令详解与应用](https://wenku.csdn.net/doc/4ycobhtu82?spm=1055.2635.3001.10343)
# 1. k-means算法基础与应用场景

## 1.1 聚类分析的定义和作用

聚类分析是数据挖掘中的一个重要技术，主要用于将数据集中的数据项划分为多个类别，使得同一类别的数据项之间相似度高，而不同类别之间的相似度低。其核心目标是让相似的对象在同一组，不相似的对象在不同的组，从而实现数据的组织和结构化，这对于后续的数据分析和处理具有重要作用。

## 1.2 聚类与分类的区别

虽然聚类和分类都是为了实现数据的分组，但它们之间存在明显差异。分类是一种监督学习方法，需要预先定义好的标签作为学习目标，而聚类是一种无监督学习方法，不依赖于预先定义的标签。简单来说，分类是给未标记数据贴上已有标签的过程，而聚类则是对未标记数据进行自然分组的过程。

## 1.3 k-means算法的应用场景

k-means算法是最常用的聚类算法之一，它的应用场景非常广泛，包括但不限于：

- 客户细分：通过分析客户消费行为、偏好等数据，将客户划分为不同群体，实现精准营销。
- 图像处理：用于图像分割，通过颜色、纹理等特征将图像中的对象划分为多个部分。
- 市场细分：在市场研究中，帮助企业理解市场的多样性和差异性。
- 生物信息学：用于基因表达数据分析、蛋白质组学等领域的数据聚类。

通过以上几个例子，我们可以看出，k-means算法在实际生活中具有广泛的应用价值，而深入理解其原理和操作，对于大数据分析和处理至关重要。

# 2. ```
# 第二章：k-means算法的理论基础

## 2.1 聚类分析概述

### 2.1.1 聚类分析的定义和作用
聚类分析是机器学习领域中的一种无监督学习方法，其核心目的是将物理或抽象对象的集合划分为由相似对象组成的多个类。聚类分析在数据挖掘、模式识别、图像分析以及市场细分中具有广泛的应用。通过聚类，可以发现数据中的内在结构和分布规律，为后续的数据分析和决策提供基础。

### 2.1.2 聚类与分类的区别
聚类与分类是机器学习中两种常见的数据处理方式。分类是监督学习的一种形式，需要基于带有标签的训练数据集来训练分类模型，以预测新数据的类别。而聚类则是无监督学习，不需要预先标记的数据。聚类的目标是基于样本之间的相似性对样本进行分组，同一组内的样本比不同组内的样本更相似。

## 2.2 k-means算法原理

### 2.2.1 k-means的工作机制
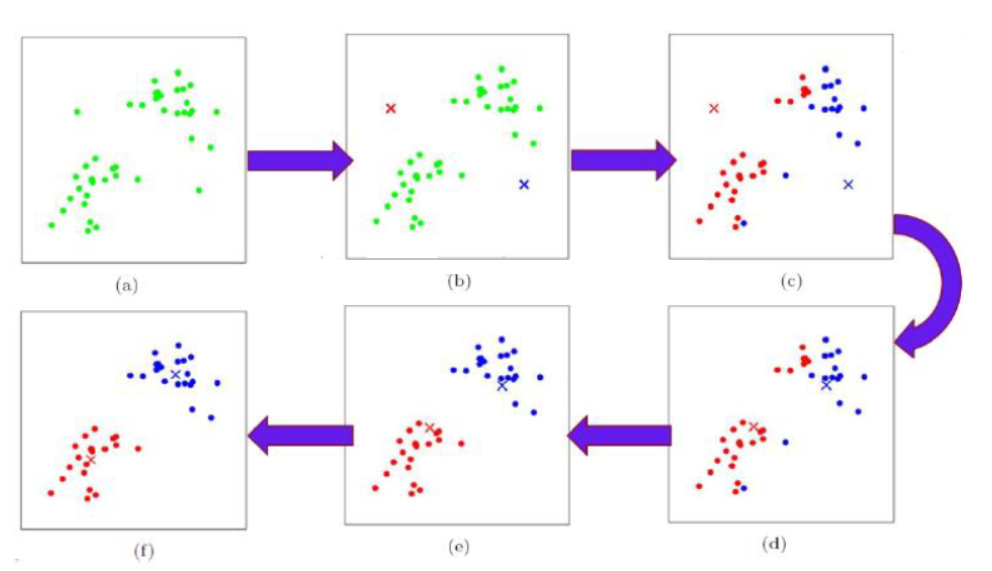
k-means算法是通过迭代的方式最小化每个点到其所属簇中心的距离之和来工作的。具体来说，算法首先随机选择k个点作为初始簇中心，然后将每个点分配给最近的簇中心，形成k个簇。接下来，算法重新计算每个簇的中心点，并重复上述过程，直到簇中心不再发生变化或满足预设的停止条件。整个过程可以用伪代码表示如下：

初始化k个簇中心
while 簇中心变化或未达到迭代次数上限 do
    将每个点分配到最近的簇中心
    对于每个簇，重新计算簇中所有点的均值作为新的簇中心
end while

### 2.2.2 距离度量方法
在k-means算法中，距离度量是核心概念之一。通常使用欧氏距离来衡量两个点之间的相似性，因为其具有良好的几何解释和数学属性。对于多维空间中的两个点x和y，它们之间的欧氏距离计算公式为：

距离(x, y) = √(∑(x_i - y_i)^2)

其中，x_i 和 y_i 分别代表点x和y在第i个维度上的值。然而，在某些特殊应用场景中，也可以使用曼哈顿距离或其他距离度量方法。

## 2.3 k-means算法的数学模型

### 2.3.1 最优聚类中心的数学推导
k-means算法的目标是找到k个中心点，使得所有数据点到其所属簇中心的距离之和最小化。这个问题在数学上可以转化为一个优化问题，即：

minimize ∑(min ||x_i - μ_j||^2)

其中，x_i 表示第i个数据点，μ_j 表示第j个簇中心，||x_i - μ_j||^2 表示x_i 到 μ_j 的欧氏距离的平方。该优化问题是一个NP难问题，但可以通过迭代的贪心算法有效近似解决。

### 2.3.2 算法的目标函数
k-means算法的目标函数是每个点到其所属簇中心距离平方和。对于k个簇，目标函数可以表示为：

J = ∑∑ ||x - μ_k||^2

其中，k表示簇的索引，x表示数据点，μ_k表示第k个簇的中心。算法的迭代过程正是通过不断优化目标函数J来找到最优解。由于目标函数是非负的，所以每次迭代都会使J值减小或保持不变，从而保证算法的收敛性。

通过以上的介绍，我们已经对k-means算法的理论基础有了一个初步的了解。接下来，我们将深入探讨k-means算法的实际操作，包括如何在数据预处理、初始化和迭代过程中具体实现k-means算法，以及如何解决算法中常见的问题。

# 3. k-means算法的实际操作与优化

在前两章中，我们已经深入探讨了k-means算法的理论基础和应用场景。现在，让我们进一步了解如何在实际操作中应用k-means算法，并且探讨一些常见的问题以及优化策略。通过实际操作和优化，可以让我们更有效地利用k-means算法解决现实世界的问题。

## 3.1 k-means算法的实现步骤

### 3.1.1 数据预处理

数据预处理是任何数据分析流程中的关键步骤，它直接影响到算法的性能和结果的准确性。对于k-means算法来说，数据预处理包括以下几个方面：

- 数据清洗：去除异常值、缺失值处理，确保数据的质量。
- 数据标准化：由于k-means算法对变量的尺度非常敏感，因此对数据进行标准化处理，使得每个维度的特征具有相同的量级是非常重要的。
- 缺失值填充：可以通过均值、中位数或者使用模型进行预测填充。

import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.impute import SimpleImputer

# 假设df是一个DataFrame对象，包含了待聚类的数据
imputer = SimpleImputer(strategy='mean')
df_filled = imputer.fit_transform(df)

scaler = StandardScaler()
df_scaled = scaler.fit_transform(df_filled)

上述代码首先使用`SimpleImputer`填充缺失值，然后使用`StandardScaler`对数据进行标准化处理。

### 3.1.2 初始化和迭代过程

k-means算法的初始化和迭代过程包括以下几个步骤：

- 随机选择k个数据点作为初始聚类中心。
- 将每个数据点分配到最近的聚类中心，形成k个簇。
- 对于每个簇，计算新的聚类中心。
- 重复上述两个步骤，直到聚类中心不再发生变化或达到最大迭代次数。

from sklearn.cluster import KMeans

# 假定k是我们要形成的簇的数量
k = 3
kmeans = KMeans(n_clusters=k, random_state=0).fit(df_scaled)

在实际操作中，可以使用`KMeans`类从`sklearn.cluster`模块来执行k-means算法。上述代码简洁地完成了整个k-means过程。

## 3.2 k-means算法的常见问题与解决方案

### 3.2.1 初始化问题

初始化问题主要表现在两个方面：初始聚类中心选择的随机性以及可能导致的局部最优问题。为了解决这个问题，我们可以采取以下措施：

- 运行算法多次，每次使用不同的随机种子。
- 使用k-means++方法进行更智能的初始化。

# 使用k-means++初始化策略
kmeans = KMeans(n_clusters=k, init='k-means++', random_state=0).fit(df_scaled)

### 3.2.2 簇的数量选择问题

簇的数量选择是k