群体行为分析：社交网络中社群识别与理解的框架

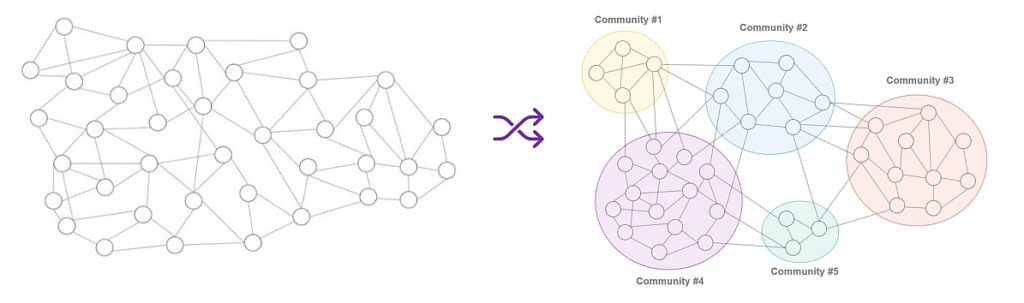
# 1. 群体行为分析概述

## 群体行为的定义与研究重要性
群体行为是社交网络研究中的一个核心议题，它涉及个体在集体环境中的互动模式及其产生的集体行为。这种分析对于理解社会动态、消费者行为、公共安全等方面都具有重要意义。了解群体行为不仅有助于刻画社会结构，还能对社会变迁和事件发展进行预测和干预。

## 研究方法与技术手段
群体行为分析通常结合定性研究和定量分析的方法。定性研究往往依靠观察、访谈等手段来获取深层次的洞察。而定量分析则借助统计学、数据挖掘、机器学习等技术手段对大规模数据进行处理，从而提取出群体行为的模式与特征。随着技术的发展，深度学习等先进算法逐渐在群体行为分析领域扮演更加重要的角色。

## 群体行为分析的应用领域
群体行为的研究成果在多个领域都有广泛应用，如市场趋势分析、公共安全事件监控、社交网络的社群管理等。通过分析群体行为，相关企业和组织可以优化决策过程，提高服务质量和市场竞争力，同时也可以更好地理解和预测社会事件。

# 2. 社交网络社群识别理论基础

在社交网络中，社群识别是发现和分析社区群体间关系的关键过程。这一章将深入探讨社群识别的概念、理论模型、数学原理及优化方法，为后续章节的技术实现和应用案例分析提供理论支撑。

### 2.1 社群识别的概念与重要性

#### 2.1.1 社群的定义与社会学视角

社群可以理解为一群个体之间存在显著的社会关系，通常围绕共同的兴趣、活动或目标形成。社会学视角强调，社群不仅是个体的简单集合，而是通过复杂的互动形成了某种凝聚力和认同感。

graph TD
    A[个体] --> B[社群]
    B --> C[凝聚力]
    B --> D[认同感]
    C --> E[共同目标]
    D --> F[共同兴趣]
    E --> G[社群行动]
    F --> H[社群活动]

在社交网络分析中，社群通常被视为由节点（用户）和边（关系）构成的图结构。识别社群的目的在于理解网络的结构和动态，以及它们如何影响信息的传播、意见的形成等社交现象。

#### 2.1.2 社群在社交网络中的作用与挑战

社群在社交网络中发挥着多方面的作用。它们可以作为信息传播的中心，影响网络内的情绪和态度，甚至可以在政治和社会运动中扮演关键角色。然而，在大规模社交网络中，社群的识别和分析面临诸多挑战。其中包括：

- 复杂网络的动态性：社交网络中社群的构成随时间变化而变化。
- 高度异构性：网络中的用户可能属于多个社群，具有多重身份。
- 社群重叠和嵌套：一些社群可能是更大社群的子集，或者多个社群可能互相重叠。
- 数据隐私和伦理问题：如何在保护用户隐私的前提下进行有效的社群识别。

### 2.2 社群识别的关键理论模型

#### 2.2.1 社群检测算法的历史发展

社群检测算法的历史发展可以追溯到20世纪60年代，当时研究者们开始探索如何从图结构中发现社区。初期研究集中在数学模型和图论算法上。1970年代到1990年代，研究者开发出了基于聚类的方法，这些方法通过测量节点间的相似性将节点分组到一起。

到了21世纪初，随着大规模社交网络的出现，出现了更多复杂和可扩展的算法，如快速社群检测算法（如Louvain方法）、基于模块度优化的方法等。这些算法在效率和准确性上都有所提高。

#### 2.2.2 当前社群识别算法综述

目前，社群识别算法主要分为几类，包括基于图聚类、基于模块度优化、层次方法、基于密度的方法等。每种方法有其优势和局限性，适用于不同的应用场景。

- **基于图聚类的方法**：如谱聚类，适用于识别任意形状的社群。
- **基于模块度优化的方法**：如Girvan-Newman算法，适用于优化社群的内部连接和外部连接。
- **层次方法**：通过合并或分割节点来构建社群的层次结构。
- **基于密度的方法**：如DBSCAN算法，通过密度差异来识别社群。

#### 2.2.3 算法的选择标准与应用场景分析

选择社群识别算法时，需要考虑以下因素：

- **数据集的规模和特征**：大规模网络可能需要可扩展的算法。
- **网络的类型**：无向网络、有向网络或加权网络，不同的网络类型适用不同的算法。
- **社群的定义**：对社群的定义将影响算法的选择，例如是否需要发现重叠社群。
- **计算效率与准确性**：在某些应用中，可以牺牲一定的准确性以获得更快的计算速度。

### 2.3 社群识别的数学原理与优化

#### 2.3.1 图论在社群识别中的应用

图论是研究图的数学理论和方法，在社群识别中具有重要应用。图可以表示为G = (V, E)，其中V是节点集合，E是边集合。社群识别的过程本质上是将图G划分为子图，每个子图代表一个社群，使得子图内部的连接紧密，而子图间的连接较为稀疏。

#### 2.3.2 优化算法与社群划分策略

优化算法在社群识别中起到核心作用。例如，模块度优化算法旨在最大化网络的模块度函数，从而识别出结构上更加紧密的社群。

Q = \frac{1}{2m} \sum_{ij} \left[ A_{ij} - \frac{k_i k_j}{2m} \right] \delta(c_i, c_j)

其中，\(Q\)是模块度，\(A_{ij}\)是邻接矩阵中的元素，\(k_i\)和\(k_j\)分别是节点i和j的度数，\(c_i\)和\(c_j\)分别表示节点i和j所在的社群，\(m\)是网络中边的总数。

社群划分策略通常涉及启发式搜索，如贪心算法，以及更加复杂的优化策略，如模拟退火和遗传算法。

通过这些数学原理和优化算法，研究者和实践者能够更精确地识别社交网络中的社群结构，进而深入分析其在传播动力学、影响力分析、群体行为预测等方面的应用。

下一章节将详细介绍社交网络社群识别技术的实现，包括实用社群检测算法的比较和社群识别工具的实际应用。

# 3. 社交网络社群识别技术实现

## 3.1 社群识别技术实践方法

### 3.1.1 实用社群检测算法的比较

在社交网络社群识别技术实践中，算法的选择至关重要。算法不仅需要能够高效准确地检测出社群结构，还应当具备良好的可扩展性和容错能力。以下是一些广泛使用的社群检测算法及其比较。

**模块度优化算法**

模块度优化是社群检测中最常用的方法之一。最著名的算法是 Newman 和 Girvan 提出的模块度最大化方法。该算法通过优化网络的模块度来识别社群，即在不考虑随机网络的情况下，最大化网络中边连接同一社群内节点的比例。该算法简单易懂，适合中小规模网络，但计算复杂度较高，不适用于大规模网络。

**层次聚类算法**

层次聚类算法将社群视为层次结构，通过合并或分裂节点来构建社群树（dendrogram）。该方法的优点是可以提供多种层级的社