R语言统计建模：Logistic回归的原理与实践

# 1. Logistic回归的基础知识

在数据分析与机器学习领域，Logistic回归是一种广泛使用的统计技术，主要用于分类问题，特别是二分类问题。它通过应用sigmoid函数，将线性回归模型的输出映射到(0,1)区间内，从而预测某一事件发生的概率。简单而言，Logistic回归可以判断某事件发生的可能性大小，这使得它在金融、医疗、市场等多个行业得到广泛应用。

## 1.1 Logistic回归的起源与发展

Logistic回归模型的起源可以追溯到19世纪末，最初被用来描述生物种群的增长过程。随后，人们发现该模型在处理分类问题中具有直观的解释性和高效性，因而逐渐被引入到统计和机器学习领域。早期的Logistic回归模型主要针对二分类问题，但随着研究的深入，模型也被扩展到了多分类问题。

## 1.2 Logistic回归的应用场景

在实际应用中，Logistic回归能够处理各种场景下的分类任务。它特别适合于那些因变量是二元的情形，如医学诊断（患病与否）、邮件筛选（垃圾邮件还是正常邮件）等。此外，由于模型的可解释性强，它常被用于初步的数据分析阶段，帮助研究人员或数据科学家快速理解变量间的相互关系。

通过以上内容，我们可以看出Logistic回归是一个既基础又强大的工具，在分类任务中占据着重要地位。接下来的章节将详细探讨Logistic回归的理论基础，并深入解析其参数估计、模型评估和R语言实现等多个方面。

# 2. ```
# 第二章：Logistic回归的理论基础

Logistic回归作为一种广泛使用的分类方法，尤其适用于因变量为二分类的情况。在深入了解其在R语言中的实现之前，我们需要掌握其背后的理论基础。

## 2.1 Logistic回归的数学原理

### 2.1.1 概率与几率

在介绍Logistic回归之前，首先要理解概率和几率的概念。概率是指某个事件发生的可能性大小，通常表示为0到1之间的数，而几率（odds）则是指事件发生与不发生的比率。在Logistic回归中，几率是被建模的变量。

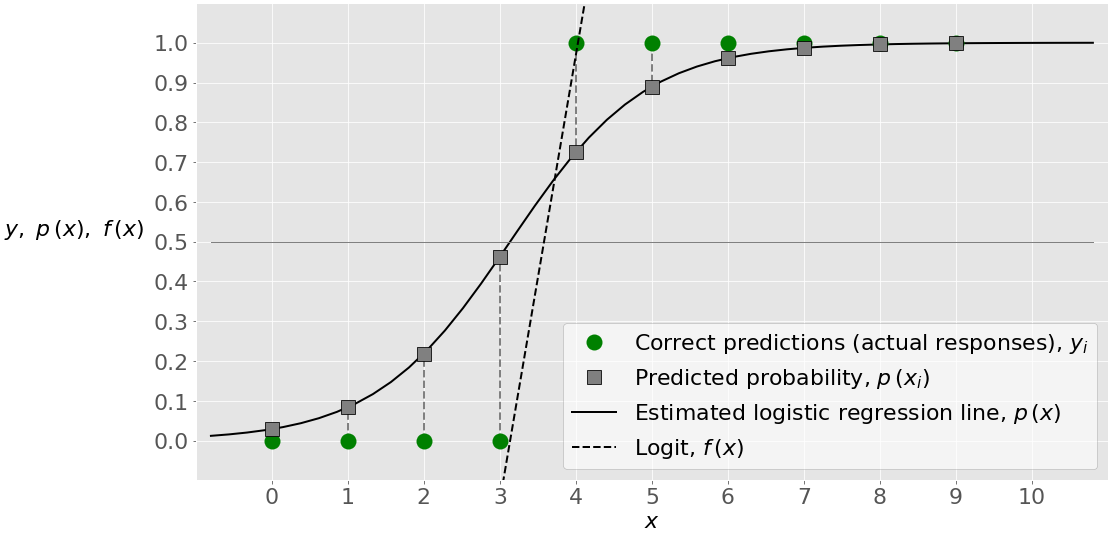
### 2.1.2 Logistic函数及其性质

Logistic回归使用的是Logistic函数（也称为sigmoid函数），该函数可以将任意实数值映射到(0,1)区间内，使之可以解释为概率。其数学表达式为：

P(Y=1) = 1 / (1 + e^-(β0 + β1X1 + ... + βkXk))

其中，P(Y=1)表示因变量为1的概率，X1至Xk是自变量，β0是截距项，β1至βk是各自变量的系数。Logistic函数具有以下性质：

- S形曲线，函数在两端趋近于0和1，中间区域变化较快。
- 函数是连续且可微的，这使得我们可以使用最优化方法来求解参数。

## 2.2 Logistic回归模型的参数估计

### 2.2.1 最大似然估计方法

参数估计是建立Logistic回归模型的关键步骤。最常用的方法是最大似然估计（Maximum Likelihood Estimation, MLE），其基本思想是选择那些能够使得观测到的数据出现的概率（似然）最大的参数值。

假设我们有n个独立的观测值，第i个观测值的因变量为Yi，自变量为Xi，则似然函数L可以定义为：

L(β) = ∏(P(Yi))^Yi * (1 - P(Yi))^(1 - Yi)

其中，P(Yi)是根据Logistic函数计算得到的。取对数似然函数，便于求最大值：

l(β) = ∑(Yi * ln(P(Yi)) + (1 - Yi) * ln(1 - P(Yi)))

通过求导并令导数为0，可以求得参数的估计值。

### 2.2.2 梯度下降法和牛顿法

求解似然方程组可能没有闭式解，因此需要借助数值优化方法。梯度下降法和牛顿法是两种常用的迭代优化算法。

梯度下降法通过不断迭代更新参数，使得似然函数值增加，直至收敛。牛顿法考虑了似然函数的二阶导数（海森矩阵），通常收敛速度更快，但计算成本较高。

## 2.3 模型的假设检验和评估

### 2.3.1 模型的显著性检验

一旦模型参数估计完毕，我们还需要检验模型中变量的统计显著性。这通常通过似然比检验、Wald检验或得分检验来完成。

- 似然比检验比较了含有和不含有某个解释变量的模型的对数似然值。
- Wald检验和得分检验则直接考察了某个参数的估计值是否显著不为0。

### 2.3.2 模型的拟合优度评价

除了对参数进行检验外，评估模型对数据的拟合程度也是必要的。常用指标包括：

- 偏差检验（Deviance Test）
- Hosmer-Lemeshow拟合优度检验
- 分类表和ROC曲线

偏差检验是比较模型与饱和模型的偏差，Hosmer-Lemeshow检验则将样本分为若干个组，比较各组预测概率的平均值与实际发生概率的差异。

分类表用于展示模型预测的准确性，ROC曲线与曲线下面积（AUC）则综合考虑了模型的灵敏度和特异性。

以上就是Logistic回归的理论基础，这些理论知识是进行实际建模工作的基础。在下一章节，我们将详细讨论如何使用R语言实现Logistic回归模型。

请注意，以上内容是一个大致的章节内容概述。在实际撰写文章时，每个章节的详细内容需要根据要求进行扩展，确保每个章节满足规定的字数要求，并提供具体的代码实现、数据分析、逻辑分析等丰富内容。

# 3. Logistic回归的R语言实现

## 3.1 R语言简介及数据准备

### 3.1.1 R语言基础环境搭建

R语言是一款流行的开源统计和图形软件，因其灵活的数据分析能力和丰富的社区支持而广受欢迎。安装R语言非常简单，只需访问官方网站下载安装包并执行即可。以下是安装R语言的基本步骤：

1. 访问 [R语言官方网站](***。
2. 选择下载镜像站点，下载适合操作系统的R语言安装文件。
3. 运行下载的安装包，并遵循安装向导完成安装。

为了方便包管理和代码编写，通常还会安装一个集成开发环境（IDE），比如RStudio。RStudio提供了代码编辑、数据操作、图形显示等功能，能够极大提升R语言的开发效率。

安装RStudio步骤如下：

1. 访问 [RStudio官网](***。
2. 选择对应操作系统的安装文件下载。
3. 运行安装包并完成安装。

安装好R语言和RStudio后，我们可以开始进行数据准备的工作，包括导入数据和数据预处理。

### 3.1.2 数据导入与预处理

在R中导入数据有多种方式，可以是文本文件、Excel、数据库等多种格式。这里以CSV格式为例，介绍如何在R中导入数据：

# 导入数据
data <- read.csv('path/to/your/data.csv', header = TRUE)

数据预处理是数据分析中的重