【从基础到高级】：一元二次方程解题全攻略，韦达定理版


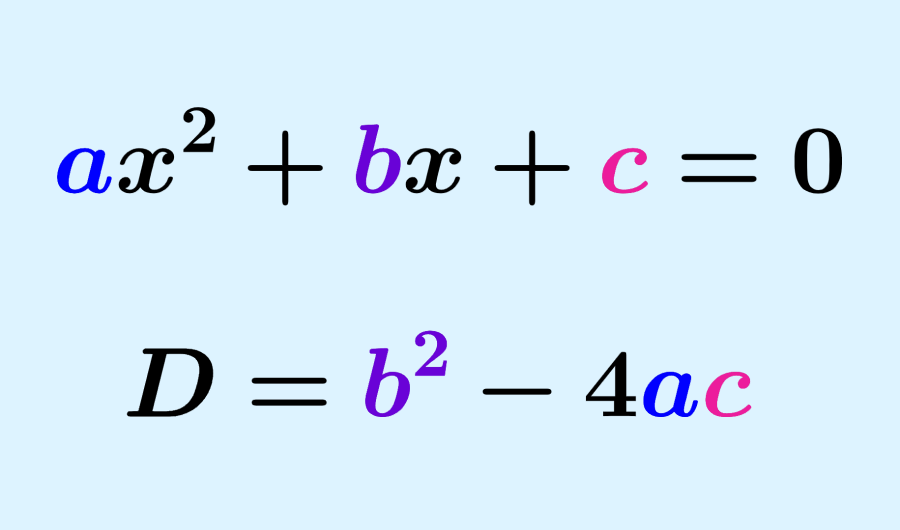
# 摘要
一元二次方程是数学中的基础概念，具备固定的标准形式和求解方法。本文系统阐述了一元二次方程的定义、传统解法、以及利用判别式和韦达定理解方程的方法。通过分析其解的性质与判别式的联系，进一步探讨了方程解的应用实例，如物理和经济学问题中的实际运用。文章还介绍了方程在函数、不等式以及复数领域的高级应用，强调了编程实践中数学函数库的使用和图形化求解器开发的可能性。整体而言，本文旨在全面覆盖一元二次方程的理论基础和实践应用，为读者提供完整的学习资源和参考。

# 关键字
一元二次方程；求根公式；判别式；韦达定理；编程应用；图形化求解器

参考资源链接：[一元二次方程解法与配方法练习](https://wenku.csdn.net/doc/35enajevfv?spm=1055.2635.3001.10343)
# 1. 一元二次方程的概念与标准形式

## 1.1 一元二次方程的基本概念

一元二次方程，顾名思义，是一个只含有一个未知数，并且未知数的最高次数为2的方程。它的一般形式可以表达为 ax² + bx + c = 0，其中a、b和c是方程的系数，且a不等于0。一元二次方程在数学以及工程、物理等学科领域中有着广泛的应用。

## 1.2 标准形式的特点

一元二次方程的标准形式是ax² + bx + c = 0。这一形式有以下几个显著特征：

- a、b、c分别代表不同的系数，其中a不为0（如果a为0，则该方程退化为一次方程）。
- x是未知数，它需要被求解。
- 该方程有两个解（包括实数解和复数解），这些解可以通过不同的数学方法得到。

## 1.3 一元二次方程的几何意义

从几何的角度来看，一元二次方程ax² + bx + c = 0所代表的是一条抛物线，该抛物线与x轴的交点对应于方程的解。如果判别式（b²-4ac）大于0，则方程有两个不同的实数解；如果判别式等于0，则有两个相同的实数解（重根）；如果判别式小于0，则方程的解为两个复数根。

graph TD;
    A[一元二次方程的一般形式 ax² + bx + c = 0] --> B[系数a、b、c的特征];
    B --> C[几何意义：抛物线与x轴的交点];
    C --> D[根据判别式判断解的类型];

以上简要介绍了关于一元二次方程的基本概念、标准形式及其几何意义。下一章节我们将深入探讨解一元二次方程的方法。

# 2. 一元二次方程的解法

一元二次方程是数学中最基本的方程之一，拥有着悠久的历史和丰富的应用。为了深入理解并掌握求解一元二次方程的方法，我们需要从不同角度来探讨和实践。本章节将介绍传统解法、判别式的运用以及利用韦达定理解方程，逐步深化我们对一元二次方程解法的认识。

## 2.1 解一元二次方程的传统方法

在数学领域，有多种传统方法可以用来解一元二次方程。这些方法包括因式分解法、完全平方法和公式法。每种方法都有其适用的场景和优缺点，掌握它们对于解决不同类型的一元二次方程非常重要。

### 2.1.1 因式分解法

因式分解法是最直观的解一元二次方程的方法之一。它的核心思想是将方程左边的多项式分解为两个一次多项式的乘积，进而求出方程的根。

考虑一元二次方程 \( ax^2 + bx + c = 0 \)，其中 \( a \neq 0 \)。当方程的根能够表示为两个一次多项式的根时，我们可以通过分解来找到它们。因式分解法的适用条件较为严格，一般要求方程可以被轻松地分解成两个一次因子。

例如，方程 \( x^2 - 5x + 6 = 0 \) 可以分解为 \( (x - 2)(x - 3) = 0 \)，从而得到解 \( x_1 = 2 \) 和 \( x_2 = 3 \)。

**代码示例**：

import sympy as sp

# 定义符号变量
x = sp.symbols('x')

# 定义方程
equation = x**2 - 5*x + 6

# 使用因式分解法求解
solutions = sp.solve(equation, x)
print(solutions)  # 输出解集

逻辑分析和参数说明：上述代码使用了 Python 的 `sympy` 库来实现因式分解法求解一元二次方程。`sympy.solve` 函数通过符号计算直接返回方程的解。

### 2.1.2 完全平方法

完全平方法是将一元二次方程转换为完全平方的形式，使得方程的左边成为某个一次式平方的形式。这个方法需要用到一个关键的代数恒等式：\( a^2 + 2ab + b^2 = (a + b)^2 \)。

例如，考虑方程 \( x^2 + 6x + 9 = 0 \)，可以将其重写为 \( (x + 3)^2 = 0 \)，从而得到解 \( x = -3 \)（重根）。

**代码示例**：

import sympy as sp

# 定义符号变量
x = sp.symbols('x')

# 定义方程
equation = x**2 + 6*x + 9

# 使用完全平方法求解
solutions = sp.solve(equation, x)
print(solutions)  # 输出解集

逻辑分析和参数说明：在上述代码中，我们首先定义了符号变量 `x` 和方程 `equation`，然后直接调用 `sympy.solve` 函数求解。在一些情况下，完全平方法可以得到直观的解，特别是在解为重根的情形下。

### 2.1.3 公式法与求根公式

公式法，又称为求根公式法，是利用代数公式直接求解一元二次方程的方法。根据方程 \( ax^2 + bx + c = 0 \) 的系数，我们可以得到一般形式的求根公式：

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

其中，\( \pm \) 表示方程有两个解，一个是加上根号里面的值，另一个是减去。求根公式适用于所有一元二次方程，并且能够直接给出精确解。

例如，对于方程 \( 2x^2 + 4x - 6 = 0 \)，应用求根公式可以得到：

\[ x = \frac{-4 \pm \sqrt{4^2 - 4 \cdot 2 \cdot (-6)}}{2 \cdot 2} = \frac{-4 \pm \sqrt{16 + 48}}{4} = \frac{-4 \pm \sqrt{64}}{4} = \frac{-4 \pm 8}{4} \]

解得 \( x_1 = 1 \) 和 \( x_2 = -3 \)。

**代码示例**：

import sympy as sp

# 定义符号变量
x = sp.symbols('x')

# 定义方程的系数
a, b, c = 2, 4, -6

# 计算判别式
discriminant = b**2 - 4*a*c

# 使用求根公式求解
solutions = [-b + sp.sqrt(discriminant), -b - sp.sqrt(discriminant)] / (2*a)
print(solutions)  # 输出解集

逻辑分析和参数说明：以上代码首先定义了符号变量 `x` 和方程的系数 `a`, `b`, `c`。然后通过计算判别式 `discriminant`，使用 Python 的 `sympy` 库来直接应用求根公式，从而得到方程的两个解。这种方法在任何情况下都是通用的。

## 2.2 判别式与一元二次方程的解的性质

判别式是判断一元二次方程根的性质的重要工具。它的计算公式为 \( \Delta = b^2 - 4ac \)，可以帮助我们了解方程根的情况。

### 2.2.1 判别式的定义与计算

判别式 \( \Delta \) 的定义取决于方程的系数 \( a \), \( b \), \( c \)。根据 \( \Delta \) 的值，我们可以得出以下结论：
- 如果 \( \Delta > 0 \)，方程有两个不同的实根；
- 如果 \( \Delta = 0 \)，方程有两个相同的实根，即一个重根；
- 如果 \( \Delta < 0 \)，方程没有实数根，而是有两个复数根。

### 2.2.2 判别式与根的关系

判别式 \( \Delta \) 的值不仅告诉我们根的性质，而且可以用来估计根的具体值。例如，当 \( \Delta > 0 \) 时，我们可以使用公式法直接求得两个实根。

**代码示例**：

import sympy as sp

# 定义符号变量
x = sp.symbols('x')

# 定义方程的系数
a, b, c = 1, -3, 2

# 计算判别式
discriminant = b**2 - 4*a*c

# 根据判别式的值来判断根的性质
if discriminant > 0:
    solutions = [(-b + sp.sqrt(discriminant)) / (2*a), (-b - sp.sqrt(discriminant)) / (2*a)]
    print("两个不同的实根:", solutions)
elif discriminant == 0:
    solutions = [-b / (2*a)]
    print("一个重根:", solutions)
else:
    print("没有实数根")

逻辑分析和参数说明：此代码段通过 `sympy` 库计算判别式，并根据其值判断根的性质，最后输出相应的解或提示信息。判别式的计算和分析是求解一元二次方程不可或缺的步骤。

## 2.3 利用韦达定理解一元二次方程

韦达定理提供了一种通过方程的系数直接确定根的和与积的方法。这个定理在解题过程中非常有用，尤其是当我们需要快速找到方程根的性质时。

### 2.3.1 韦达定理的表述

韦达定理指出，对于一般形式的一元二次方程 \( ax^2 + bx + c = 0 \)（\( a \neq 0 \)），其解 \( x_1 \) 和 \( x_2 \) 满足以下关系：
- \( x_1 + x_2 = -\frac{b}{a} \)
- \( x_1 \cdot x_2 = \frac{c}{a} \)

### 2.3.2 应用韦达定理解方程实例

利用韦达定理可以快速得到方程根的和与积，而不必求出具体的根。例如，对于方程 \( 3x^2 + 6x + 2 = 0 \)，我们可以直接写出：
\[ x_1 + x_2 = -\frac{6}{3} = -2 \]
\[ x_1 \cdot x_2 = \frac{2}{3} \]

这为我们快速分析方程的根提供了便捷。

**代码示例**：

import sympy as sp

# 定义符号变量
x = sp.symbols('x')

# 定义方程的系数
a, b, c = 3, 6, 2

# 应用韦达定理求根的和与积
root_sum = -b / a
root_product = c / a
print(f"根的和为: {root_sum}")
print(f"根的积为: {root_product}")

逻辑分析和参数说明：通过定义符号变量 `x` 和方程的系数 `a`, `b`, `c`，直接使用 `sympy` 库中的算术操作来计算根的和与积。这展示了韦达定理在快速分析方程根方面的实用性。

通过本章节的讨论，我们已经了解了多种解一元二次方程的方法。接下来的章节，我们将进一步探讨一元二次方程解的性质，以及如何将其应用于实际问题中。

# 3. 一元二次方程解题实战演练

## 3.1 应用一元二次方程解决实际问题

在前两章中，我们已经详细介绍了关于一元二次方程的概念、解法及其性质。本章节将进入实战演练阶段，我们将通过解决具体的实际问题来应用我们所学的一元二次方程的知识。

### 3.1.1 物理问题中的应用

物理学中有许多通过建立数学模型来解决的问题，而一元二次方程是这些模型中常用的数学工具之一。例如，在研究物体抛体运动的轨迹时，可以借助一元二次方程来描述其运动方程。

假设有一个物体从地面以一定的初速度v0以角度θ投射出去，忽略空气阻力，通过分析可以得出物体的运动轨迹方程是一元二次方程：

\[ y = x \tan(\theta) - \frac{g}{2v_0^2 \cos^2(\theta)} x^2 \]

这里g是重力加速度。通过这个方程，我们不仅能求出物体达到的最大高度，还能预测物体在不同时间的水平距离。

**代码示例：**

import math

# 投射角度（弧度）
theta = math.radians(45)
# 初速度（m/s）
v0 = 20
# 重力加速度（m/s^2）
g = 9.81

# 最大高度计算公式
def max_height(v0, theta, g):
    return (v0**2 * math.sin(theta)**2) / (2*g)

# 最大高度
max_h = max_height(v0, theta, g)

print(f"The maximum height reached by the object is {max_h:.2f} meters.")

在这个代码块中，我们定义了一个函数`max_height`来计算物体的最大高度，然后用具体数值调用函数并打印结果。

### 3.1.2 经济学中的应用

在经济学领域，一元二次方程也可用于分析成本、收益、价格等的变动情况。例如，生产成本和生产量之间的关系模型可以用一元二次方程来表示，从而帮助经济学家和企业家确定生产策略。

假设一个产品的生产成本C与生产数量q之间的关系可以用一元二次方程表示：

\[ C(q) = aq^2 + bq + c \]

其中a、b、c为常数，分别表示生产过程中变动成本、固定成本和其它成本。通过解这个方程，企业能够了解在不同的生产量下，成本是如何变化的，从而对生产计划进行调整。

**代码示例：**

# 成本函数
def cost_function(q, a, b, c):
    return a*q**2 + b*q + c

# 成本参数
a = 10
b = 50
c = 100

# 不同生产量下的成本
quantities = [0, 5, 10, 15, 20]
for q in quantities:
    cost = cost_function(q, a, b, c)
    print(f"Production quantity: {q}, Total cost: {cost:.2f}")

在这个例子中，我们定义了一个成本函数`cost_function`来计算生产不同数量产品的总成本。然后，我们为不同的生产量调用该函数，打印出相应的成本信息。

## 3.2 解题技巧与常见误区分析

### 3.2.1 解题过程中的常见错误

在解决一元二次方程问题的过程中，学生和初学者常常会犯一些典型错误。例如，很多人在使用求根公式时容易记错公式或者搞混根的顺序，导致计算错误。另一个常见问题是忽视判别式的正负对解的影响，不理解判别式与根的关系，从而在方程无实数解的情况下错误地给出答案。

**重要的是**，在解方程之前，一定要检查判别式D（\(D = b^2 - 4ac\)），并判断其是否大于等于零。如果D小于零，那么方程没有实数解，此时若仍然继续求解，将会得到无意义的复数解。

### 3.2.2 提高解题效率的技巧

为了提高解题效率，有一些技巧可以使用：

1. **识别方程类型：** 熟悉各种问题情境下如何快速识别一元二次方程的形式。
2. **记忆公式：** 公式法的运用是解一元二次方程的基本技巧，需要熟练掌握和运用。
3. **简化题目：** 当方程形式复杂时，尝试通过代数变换简化它。
4. **检查答案：** 每次解方程后，将根代入原方程进行验证。

**实践这些技巧**，不仅可以提升解题的速度，还能提高准确度。例如，当面对一个一元二次方程时，我们首先应该做的就是通过因式分解、完全平方法或者使用求根公式简化和解决方程。

**一个有效的解题流程如下：**

- 确定方程标准形式。
- 计算判别式D。
- 根据D的值确定方程的根的类型（实数解或复数解）。
- 应用适当的方法求出方程的根（实根或复根）。
- 检查和验证答案。

**实际应用：**

graph TD;
    A[Start] --> B[确定方程的标准形式];
    B --> C[计算判别式D];
    C -->|D>=0| D[使用求根公式求实根];
    C -->|D<0| E[使用复数根公式求解];
    D --> F[检查答案];
    E --> F;
    F --> G[结束解题流程];

在上述的流程图中，我们可以看到一个清晰的一元二次方程的解题流程，这有助于我们在实际解题时有条不紊地进行。通过这样的练习，我们会对问题有更深入的理解，从而在实战演练中达到更好的效果。

# 4. 一元二次方程的高级应用

## 4.1 一元二次方程在函数中的应用

### 4.1.1 抛物线与一元二次方程

在数学中，抛物线是一种与一元二次方程密切相关的二次函数图形。抛物线的方程通常表示为 \(y=ax^2+bx+c\)，其中 \(a\)、\(b\) 和 \(c\) 是常数，且 \(a \neq 0\)。这种形式的方程与一元二次方程的标准形式 \(ax^2+bx+c=0\) 密切相关，但前者描述的是实数域上所有可能的 \(x\) 值对应的 \(y\) 值，而后者专门描述方程为零时 \(x\) 的情况。

抛物线具有以下特征：

- **对称轴**：通过抛物线顶点的垂直线称为对称轴。对于一般形式的抛物线方程，对称轴的方程可以表示为 \(x=-\frac{b}{2a}\)。
- **顶点**：抛物线的最高点或最低点称为顶点。顶点的坐标可以通过对称轴的方程和抛物线方程计算得到。
- **开口方向**：抛物线开口向上，如果 \(a>0\)；开口向下，如果 \(a<0\)。
- **焦点**：抛物线上任意一点到焦点的距离等于该点到对称轴的距离。焦点的坐标为 \((h,k\pm\frac{1}{4a})\)，其中 \(h\) 和 \(k\) 分别是顶点的 \(x\) 和 \(y\) 坐标。

这些几何特征是分析和解决一元二次方程相关问题的关键。

### 4.1.2 顶点与焦点的计算

顶点的坐标 \((h,k)\) 可以直接从抛物线方程 \(y=ax^2+bx+c\) 中计算得到，公式如下：

\[ h = -\frac{b}{2a} \]
\[ k = c - \frac{b^2}{4a} \]

顶点可以告诉我们抛物线的最高点或最低点的位置，这是分析抛物线行为的重要信息。

焦点的坐标对于理解抛物线的对称性非常关键。根据焦点公式，焦点的位置可以通过顶点坐标和 \(a\) 的值计算得到。由于抛物线的对称性，我们可以利用顶点和 \(a\) 的值，找到抛物线上任意一点与焦点之间的关系。这在物理学中，如抛物线运动轨迹的应用，是非常重要的。

## 4.2 一元二次方程与不等式

### 4.2.1 解不等式的策略

解不等式是数学分析中的一个重要部分，特别是一元二次不等式。对于不等式 \(ax^2+bx+c>0\) 或 \(ax^2+bx+c<0\) 的解集，我们通常采用以下策略：

1. **因式分解**：如果可能的话，首先尝试将不等式因式分解。这将帮助我们将不等式转换为更简单的一元一次不等式，从而更容易解决。
2. **找出临界点**：通过设置 \(ax^2+bx+c=0\) 找出临界点，这些临界点就是不等式解集的边界。
3. **分析区间**：在临界点将数轴分成若干区间，确定哪些区间满足原不等式的条件。
4. **考虑开口方向**：根据 \(a\) 的正负，确定不等式解集的开口方向。
5. **得出结论**：根据上述分析得出最终的解集。

### 4.2.2 一元二次不等式的解法

考虑一个一般形式的一元二次不等式 \(ax^2+bx+c>0\)（\(a>0\)）：

1. **找出临界点**：求解方程 \(ax^2+bx+c=0\)，得到临界点 \(x_1\) 和 \(x_2\)。
2. **判断开口方向**：因为 \(a>0\)，抛物线开口向上。
3. **分析解集**：由于抛物线开口向上，不等式 \(ax^2+bx+c>0\) 的解集是两个临界点之间的开区间 \(x \in (x_1, x_2)\)，或者当 \(b^2-4ac<0\) 时，解集是所有实数 \(x \in \mathbb{R}\)。

对于 \(a<0\) 的情况，解集会在区间 \((x_2, x_1)\) 或者不存在实数解集（\(b^2-4ac<0\)）。

from sympy import symbols, Eq, solve

# 定义变量
x = symbols('x')

# 定义系数
a, b, c = 1, -3, 2

# 创建方程
equation = Eq(a*x**2 + b*x + c, 0)

# 求解方程
solutions = solve(equation, x)

print(f"临界点为: {solutions}")

在此代码块中，我们使用 Python 的 `sympy` 库来求解一元二次不等式。首先，我们导入必要的符号和函数，然后定义方程的系数，并创建一个等式方程对象。最后，我们调用 `solve` 函数求解方程的根。

graph TD
A[开始求解] --> B[定义符号]
B --> C[设置系数]
C --> D[创建方程对象]
D --> E[求解方程]
E --> F[输出结果]

根据上述步骤，我们能够找到临界点，并且通过进一步分析不等式的开口方向和符号，确定不等式的解集。

# 5. 一元二次方程的拓展内容

## 5.1 复数根与一元二次方程

一元二次方程在实数域内的解可能有两个实根、一个实根或没有实根，而当引入复数根的概念后，任何一元二次方程总是有两个根（包括重根）。理解复数的概念，对于深入探索数学世界，特别是在解决涉及平方根的负数问题时，显得尤为重要。

### 5.1.1 复数的概念

复数的引入源于对负数开平方的需要。一个复数通常写作`a + bi`，其中`a`和`b`是实数，而`i`是虚数单位，满足`i^2 = -1`。复数集是实数集的扩展，它包括所有实数和所有纯虚数。复数的加、减、乘、除运算遵循特定的规则，例如加法是实部与实部相加，虚部与虚部相加；乘法则是将两个复数的模相乘，和它们的角度相加。

### 5.1.2 复数根的求解及应用

对于一元二次方程`ax^2 + bx + c = 0`，当判别式`D = b^2 - 4ac < 0`时，方程没有实数解，但有两个共轭的复数根。使用求根公式，可以得到这两个复数根：

x1, x2 = (-b ± sqrt(D)i) / (2a)

例如，考虑方程`x^2 + 1 = 0`，它的判别式为`-4`，是负数，所以它有两个复数根：`x1 = i`和`x2 = -i`。复数根在物理、工程学等领域中非常有用，尤其在描述波动现象，如交流电和声音波动时。

import cmath

# 定义方程参数
a = 1
b = 0
c = 1

# 计算判别式
D = b**2 - 4*a*c

# 计算复数根
x1 = (-b + cmath.sqrt(D)) / (2*a)
x2 = (-b - cmath.sqrt(D)) / (2*a)

print(f"The roots of the equation are complex numbers: {x1} and {x2}")

通过以上Python代码，我们使用了`cmath`模块来处理包含复数的数学运算。这段代码不仅计算出了一元二次方程的复数根，而且展示了复数在编程中的应用。

## 5.2 一元二次方程与其他数学分支的联系

一元二次方程并非孤立的数学概念，它与其他数学分支有着广泛的联系。了解这些联系有助于我们更好地理解数学的统一性和美妙。

### 5.2.1 几何学中的应用

在平面解析几何中，一元二次方程通常用于描述抛物线形状。抛物线的方程可以是`y = ax^2 + bx + c`或`x = ay^2 + by + c`，取决于选择的坐标轴。抛物线与一元二次方程的关系，使得我们可以从几何角度来研究方程的性质，比如顶点的位置、焦点和准线的计算等。

考虑方程`y = ax^2 + bx + c`，其对称轴的位置为`x = -b / (2a)`，顶点的高度为`y = c - b^2 / (4a)`。这些几何属性帮助我们直观地理解方程的解及其图像。

### 5.2.2 概率与统计中的应用

在概率论中，一元二次方程的解可以帮助我们找到某些分布的极值点，如正态分布的概率密度函数的最大值点。此外，在统计学中，最小二乘法用于拟合数据到直线或曲线（如抛物线），其基础计算过程往往涉及到一元二次方程。

例如，如果我们有一组数据点，我们可以通过最小二乘法找到拟合这些点的抛物线`y = ax^2 + bx + c`的系数`a`、`b`和`c`，从而找到最佳拟合曲线。这一过程在数据分析、预测建模等领域中极其重要。

通过本章节的深入探索，我们不仅扩大了对一元二次方程的理解，也建立了它与其他数学领域的联系。了解复数根的概念和几何、统计学中的应用，有助于我们全面认识这一方程的内涵和外延。

# 6. 一元二次方程的编程应用

## 6.1 编程语言中的数学函数库

在软件开发过程中，处理数学问题常常需要借助强大的数学库来简化计算，提高效率。对于一元二次方程而言，编程语言中的数学函数库提供了便捷的工具来实现求解。

### 6.1.1 Python的数学库应用

Python提供了多种数学相关的库，其中`math`模块是最基础的数学库，包含了诸如平方根、三角函数等基础数学运算。若要处理更高级的数学运算，如求解一元二次方程的根，可以使用`numpy`或`sympy`库。

import numpy as np

# 定义一元二次方程的系数
a, b, c = 1, -3, 2

# 使用numpy的roots函数求解
roots = np.roots([a, b, c])

print(f"The roots are: {roots}")

上述代码通过`numpy.roots`函数直接计算出一元二次方程的根。无需手动实现复杂的求根公式，借助数学库的封装，可以非常简洁地完成计算。

### 6.1.2 C++的数值计算库应用

C++社区同样提供了多个高质量的数值计算库，比如`Armadillo`、`Eigen`和`Boost.Multiprecision`等。通过这些库，我们可以在C++中轻松实现高精度和复杂的数学运算。

#include <iostream>
#include <boost/multiprecision/cpp_dec_float.hpp>

int main() {
    typedef boost::multiprecision::cpp_dec_float_100 Float;

    // 定义一元二次方程的系数
    Float a = 1, b = -3, c = 2;

    // 判别式
    Float D = b * b - 4 * a * c;

    if (D >= 0) {
        // 两个实数解
        Float sqrt_D = sqrt(D);
        Float root1 = (-b + sqrt_D) / (2 * a);
        Float root2 = (-b - sqrt_D) / (2 * a);
        std::cout << "Roots: " << root1 << " and " << root2 << std::endl;
    } else {
        // 两个复数解
        Float sqrt_D = sqrt(-D);
        Float real_part = -b / (2 * a);
        Float imaginary_part = sqrt_D / (2 * a);
        std::cout << "Roots: " << real_part << " + " << imaginary_part << "i and " << real_part << " - " << imaginary_part << "i" << std::endl;
    }

    return 0;
}

这段代码使用了Boost库中的`cpp_dec_float`来处理高精度的浮点数运算，因此即使是在复数范围内，也能得到精确的结果。

## 6.2 创新编程实践：图形化求解器开发

图形化用户界面（GUI）是提高用户体验的重要方式之一。在开发一元二次方程求解器的软件时，融入图形化界面可以更直观地展示结果，使得非专业用户也能方便地使用。

### 6.2.1 需求分析与设计

在设计图形化求解器时，需要考虑以下几个关键点：
- 用户输入方程系数的途径（文本框、数字输入框等）。
- 计算按钮，用于触发求解算法。
- 结果展示方式（文本框、弹出提示、图形显示等）。
- 用户交互流程，确保用户易于理解和操作。

### 6.2.2 界面设计与功能实现

假设我们使用Python的Tkinter库来设计GUI，以下是实现一个基础的一元二次方程求解器GUI的代码示例：

import tkinter as tk
from tkinter import messagebox

def solve_quadratic_equation():
    try:
        # 获取输入值
        a = float(entry_a.get())
        b = float(entry_b.get())
        c = float(entry_c.get())
        # 计算判别式
        discriminant = b**2 - 4*a*c
        if discriminant < 0:
            messagebox.showerror("Error", "The equation has no real roots.")
            return
        # 计算根
        root1 = (-b + discriminant**0.5) / (2*a)
        root2 = (-b - discriminant**0.5) / (2*a)
        # 显示结果
        result = f"Roots: {root1}, {root2}"
        messagebox.showinfo("Results", result)
    except ValueError:
        messagebox.showerror("Error", "Please enter valid numbers.")

# 创建窗口
window = tk.Tk()
window.title("Quadratic Equation Solver")

# 创建输入框、标签和按钮
label_a = tk.Label(window, text="a:")
label_a.grid(row=0, column=0)

entry_a = tk.Entry(window)
entry_a.grid(row=0, column=1)

label_b = tk.Label(window, text="b:")
label_b.grid(row=1, column=0)

entry_b = tk.Entry(window)
entry_b.grid(row=1, column=1)

label_c = tk.Label(window, text="c:")
label_c.grid(row=2, column=0)

entry_c = tk.Entry(window)
entry_c.grid(row=2, column=1)

solve_button = tk.Button(window, text="Solve", command=solve_quadratic_equation)
solve_button.grid(row=3, column=0, columnspan=2)

# 运行主循环
window.mainloop()

上述代码展示了一个基本的一元二次方程求解器的GUI界面，它允许用户输入系数，点击求解按钮后，若方程有实数解，则弹出一个窗口显示方程的根。

通过上述示例，可以发现图形化界面的加入极大地提升了软件的可用性和交互性，尤其对于那些不熟悉命令行操作的用户来说，这是一个非常友好的改进。