【韦达定理的图形解析】：直观理解一元二次方程的根


# 摘要
韦达定理作为数学中基础而重要的理论之一，它建立了方程系数与根之间的关系，并在数学的多个分支中有着广泛的应用。本文首先回顾了韦达定理的基本概念及其在数学史上的地位，随后深入探讨了一元二次方程的理论，包括其标准形式、根与系数的关系以及解的存在条件。通过图形解析方法，将韦达定理与一元二次函数图像联系起来，直观展示根的几何意义。此外，本文还提供了韦达定理在代数题目和实际问题解决中的具体应用实例，并对其在高级数学中的拓展进行了探讨。本文旨在通过对韦达定理的全面分析，加深对其理论深度和实际应用的认识，为数学研究及教育提供参考。
# 关键字
韦达定理；一元二次方程；图形解析；根与系数；代数应用；高级数学拓展

参考资源链接：[一元二次方程解法与配方法练习](https://wenku.csdn.net/doc/35enajevfv?spm=1055.2635.3001.10343)
# 1. 韦达定理的基本概念与历史

## 1.1 韦达定理的起源与发展
韦达定理是16世纪法国数学家弗朗索瓦·韦达（Francois Viete）提出的，是解决一元二次方程根问题的一个重要工具。它揭示了方程根与系数之间的关系，即方程的两个根之和等于系数之比，两个根的积等于常数项。这个定理不仅简化了方程求解过程，还在数学领域内推动了解析几何与代数方程的发展。

## 1.2 韦达定理的现代意义
随着时间的推移，韦达定理已经成为数学教育的基础内容之一，它不仅仅局限于一元二次方程的解法，还扩展到更广泛的数学领域，如代数方程组、多项式理论、以及解析几何。韦达定理的概念在物理、工程和经济学中也有广泛的应用，帮助理解和解决实际问题。

## 1.3 章节总结
在本章中，我们介绍了韦达定理的起源、发展及其在现代数学和科学中的重要地位。通过本章的学习，读者将对韦达定理有一个全面的了解，并为进一步探索其在更复杂问题中的应用打下坚实的基础。下一章将深入探讨一元二次方程的数学理论基础，为读者提供更丰富的数学背景知识。

# 2. 一元二次方程的数学理论

### 2.1 一元二次方程的定义与标准形式

#### 2.1.1 方程的标准形式解析

一元二次方程是数学中的基本方程形式之一，其标准形式可以表示为 ax^2 + bx + c = 0，其中 a、b、c 是系数，且 a ≠ 0。为了方便理解和处理，通常我们会将一元二次方程化为标准形式，使得方程的左侧没有一次项和常数项，右侧为零。

化为标准形式的过程通常包括移项和合并同类项两个步骤。例如，方程 3x^2 + 6x - 9 = 0 是一元二次方程的标准形式，而 x^2 + 2x - 3 = 4 可以经过移项得到 x^2 + 2x - 7 = 0，这就是它的标准形式。

在标准形式中，二次项系数 a 决定了抛物线开口方向和宽度，一次项系数 b 决定抛物线顶点的横坐标，常数项 c 则影响抛物线顶点的纵坐标位置。

#### 2.1.2 系数与常数项的意义

在一元二次方程中，系数 a、b、c 都承载着特定的数学意义和几何意义。系数 a 决定了抛物线的开口方向和宽度，当 a > 0 时，抛物线开口向上；当 a < 0 时，开口向下。此外，a 的绝对值大小也决定了抛物线的宽度，a 的绝对值越大，抛物线越窄。

一次项系数 b 与 a 一起决定了抛物线顶点的位置。具体来说，抛物线顶点的横坐标 x 可以通过公式 -b / (2a) 得出。常数项 c 影响着抛物线与 y 轴的交点，即顶点的纵坐标，可以理解为抛物线在 y 轴上的截距。

### 2.2 根与系数的关系——韦达定理

#### 2.2.1 根的和与根的积的推导

韦达定理是描述一元二次方程根与系数关系的数学定理。如果一元二次方程 ax^2 + bx + c = 0 的两个根为 x₁ 和 x₂，则韦达定理表明根的和 x₁ + x₂ = -b/a，根的积 x₁x₂ = c/a。

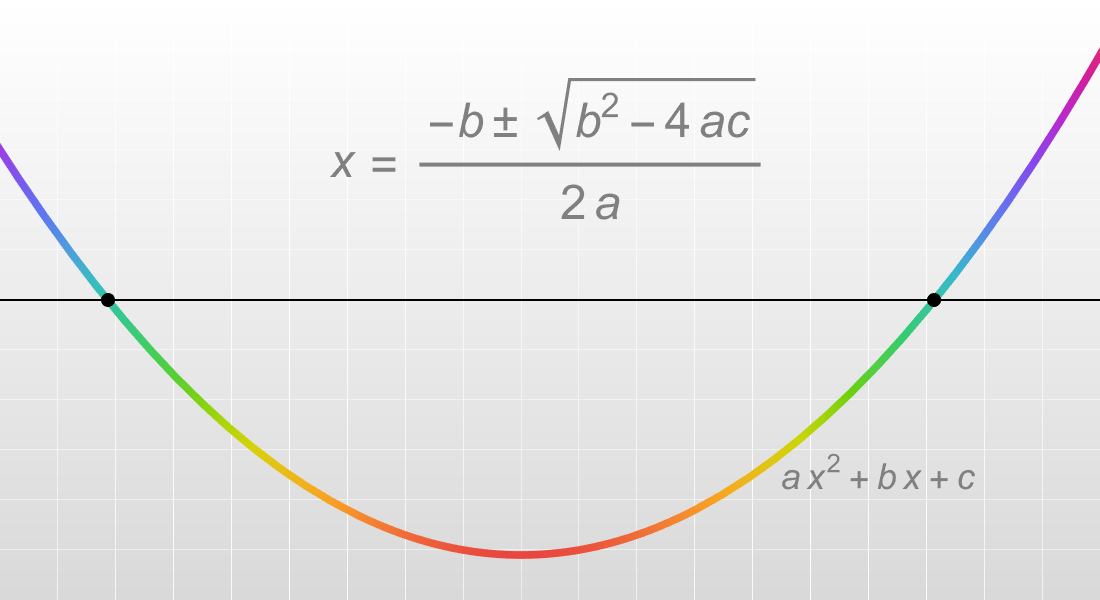
推导过程可以通过配方法或直接应用求根公式。首先，将方程写成 x = [-b ± √(b^2 - 4ac)] / (2a) 的形式，然后分别取 ± 两侧的值进行加减运算，即可得到根的和和根的积的表达式。

#### 2.2.2 韦达定理在不同方程中的表现

韦达定理在不同的方程中可以有不同的表现形式。对于带有特殊系数的方程，如完全平方的一元二次方程，韦达定理可以简化根的表达式。例如，方程 (x - p)^2 = 0 的根为 x₁ = x₂ = p，此时根的和为 2p，根的积为 p^2，满足韦达定理。

另外，对于一些没有实际解的方程，即当判别式 Δ = b^2 - 4ac < 0 时，方程没有实数根，但韦达定理依然成立，根的和与积为虚数形式，体现了韦达定理在复数域内的拓展性。

### 2.3 一元二次方程解的存在条件

#### 2.3.1 判别式与方程根的性质

一元二次方程的解存在条件通常通过判别式来判断。判别式 Δ 定义为 Δ = b^2 - 4ac。根据判别式的值，可以决定方程的根的性质：

- 当 Δ > 0 时，方程有两个不同的实数根；
- 当 Δ = 0 时，方程有两个相同的实数根，也就是一个重根；
- 当 Δ < 0 时，方程没有实数根，但有两个复数根。

这个性质非常关键，它允许我们通过计算判别式的值，快速判断方程根的性质。

#### 2.3.2 根的不同情况分析

对于一元二次方程的根的不同情况，我们可以进行更深入的分析。对于 Δ > 0 的情况，根的性质是完全确定的，两个根都是实数，而且是唯一的。对于 Δ = 0 的情况，虽然方程的解是重根，但仍然可以视作一个单一解。

对于 Δ < 0 的情况，虽然没有实数根，但这并不意味着方程没有解。而是解以复数的形式存在。例如，方程 x^2 + x + 1 = 0 的判别式为 Δ = 1^2 - 4*1*1 = -3 < 0，因此它有两个复数根 x₁ = (-1 + √3i) / 2 和 x₂ = (-1 - √3i) / 2。

这种情况下，复数根的和和积依然遵循韦达定理，即 x₁ + x₂ = -b/a 和 x₁x₂ = c/a。这意味着韦达定理在实数域和复数域内均适用，提供了一种对复数根进行简单计算的方法。

### 代码块解释与分析

为了更好地理解和应用韦达定理，我们可以编写一段代码，用以计算一元二次方程的根，以及验证判别式和韦达定理的关系。以下是一个简单的 Python 示例：

import cmath

# 定义一个函数来求解一元二次方程的根
def solve_quadratic(a, b, c):
    # 计算判别式
    delta = cmath.sqrt(b**2 - 4*a*c)
    # 计算两个根
    root1 = (-b + delta) / (2*a)
    root2 = (-b - delta) / (2*a)
    return (root1, root2)

# 示例：求解方程 x^2 + 2x + 5 = 0 的根
roots = solve_quadratic(1, 2, 5)
print("The roots of the equation are:", roots)

在这段代码中，我们首先导入了 Python 的 `cmath` 模块，它提供了对复数的数学运算支持。接着，我们定义了一个函数 `