无线通信质量保证:低通滤波器在信号中的关键作用
发布时间: 2024-12-22 06:14:50 阅读量: 10 订阅数: 13 


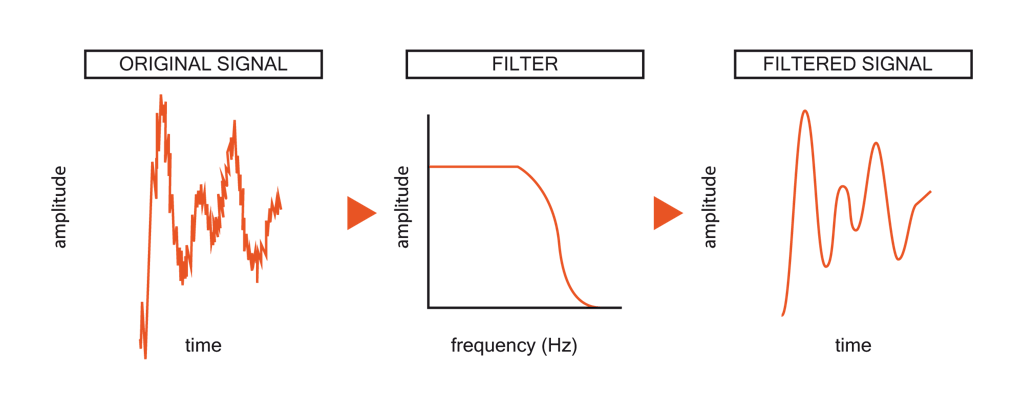
RFID技术中的射频接口芯片低通滤波器的选择
# 摘要
随着无线通信技术的快速发展,信号处理质量面临更多挑战。本文综述了无线通信的基本概念及其质量挑战,并深入探讨了低通滤波器的理论基础和设计实现。通过分析低通滤波器的设计、关键参数及其在无线通信中的应用,本文展示了如何有效解决信号干扰、选择和带宽调整问题。此外,本文还讨论了低通滤波器性能的评估方法和常见问题的优化策略,最后展望了低通滤波器在5G及未来通信技术中的潜在应用,以及智能算法和机器学习技术在滤波器设计中可能带来的革新。
# 关键字
无线通信;低通滤波器;信号处理;滤波器设计;通信质量;机器学习
参考资源链接:[PSIM仿真结果分析:FFT数据导出与Excel处理](https://wenku.csdn.net/doc/7on276eskx?spm=1055.2635.3001.10343)
# 1. 无线通信概述及质量挑战
## 1.1 无线通信发展背景
无线通信技术自问世以来,已成为现代社会不可或缺的一部分。它使得信息的传输摆脱了有线媒介的束缚,实现了全球范围内的即时通信。随着智能手机、物联网(IoT)、自动驾驶汽车等技术的发展,无线通信的需求也在爆炸式增长,这就对无线信号的传输质量提出了更高的挑战。
## 1.2 无线信号的质量挑战
无线通信面临诸多质量挑战,包括多径效应、信号干扰、带宽限制等。这些问题往往会导致信号失真和噪声增加,降低通信效率和数据传输的准确性。为了克服这些挑战,无线通信系统需要使用各种技术手段来优化信号质量。
## 1.3 低通滤波器的角色
在这其中,低通滤波器扮演了至关重要的角色。低通滤波器可以有效地去除高频噪声,保证信号在传输过程中的一致性和纯净性。在下一章节中,我们将深入探讨低通滤波器的理论基础,以及它在无线通信中的应用和设计。
# 2. 低通滤波器的理论基础
### 2.1 信号处理中的滤波器简介
低通滤波器是电子信号处理中不可或缺的组件之一,它们能够允许特定频率范围内的信号通过,同时阻止或减弱高于该范围的频率信号。本节将对滤波器的定义、分类以及其在无线通信中的作用进行深入探讨。
#### 2.1.1 滤波器的定义与分类
滤波器(Filter)是一种电子设备或计算过程,其主要目的是对信号进行修改,以便通过或者阻止特定频率的信号。根据处理信号的类型,滤波器可以分为模拟滤波器和数字滤波器两大类。模拟滤波器处理连续的信号,而数字滤波器处理离散的信号,通常在数字信号处理器(DSP)上实现。
在分类上,滤波器主要分为四种基本类型:
- 低通滤波器(LPF):允许低频信号通过,阻止高频信号。
- 高通滤波器(HPF):允许高频信号通过,阻止低频信号。
- 带通滤波器(BPF):允许一定频带范围内的信号通过,阻止其他频段的信号。
- 带阻滤波器(BRF)或陷波滤波器:阻止一定频带范围内的信号通过,允许其他频段的信号。
#### 2.1.2 滤波器在无线通信中的作用
在无线通信中,滤波器的作用至关重要。由于无线频谱资源有限,且不同频率的信号会相互干扰,因此使用滤波器对信号进行选择性传输和接收变得至关重要。低通滤波器尤其适用于抑制高频噪声,提升通信质量。
在发送端,滤波器可以确保信号在规定的频率范围内,防止信号的带外辐射,即防止不符合规定频率范围的信号成分泄漏到频谱中。在接收端,低通滤波器能够抑制带宽外的干扰,提高信号的信噪比。
### 2.2 低通滤波器的工作原理
低通滤波器的工作原理是基于其截止频率的概念。本节将介绍截止频率、传递函数以及滤波器阶数对性能的影响。
#### 2.2.1 截止频率的概念
截止频率是指滤波器开始显著抑制信号通过的频率点。对于低通滤波器而言,它允许低于截止频率的信号无阻碍地通过,而高于截止频率的信号将被削弱到某个特定的水平。
例如,如果一个低通滤波器的截止频率设为300Hz,那么低于300Hz的信号将几乎不受影响,而高于300Hz的信号将被逐渐减弱。这种减弱通常通过一个斜率(或称为滚降系数)来描述,表明信号衰减的程度。
#### 2.2.2 低通滤波器的传递函数
传递函数是数学上描述滤波器对输入信号进行处理后输出信号的方程式。对于低通滤波器,其传递函数通常具有以下形式:
\[ H(s) = \frac{K}{1 + \frac{s}{\omega_0}} \]
其中,\( H(s) \) 是滤波器的传递函数,\( K \) 是增益常数,\( s \) 是复频率变量,\( \omega_0 \) 是截止频率。
此传递函数表明,在截止频率以下,\( H(s) \) 接近于常数 \( K \),表示信号几乎无衰减。而当频率大于 \( \omega_0 \) 时,传递函数开始下降,信号开始衰减。
#### 2.2.3 滤波器阶数与性能的关系
滤波器的阶数(或称为阶)指滤波器中能量存储元件(如电容器和电感器)的数量。它决定了滤波器频率响应的陡峭程度。一般来说,阶数越高,滤波器的截止斜率越陡,但会引入更多的相位失真。
例如,一阶低通滤波器在截止频率处的斜率大约为-20dB/10倍频程。二阶滤波器可以提供-40dB/10倍频程的斜率,因此,二阶滤波器在截止频率附近能够更快地衰减信号。
### 2.3 滤波器设计的关键参数
设计滤波器时需要考虑到许多因素,以确保滤波器在实际应用中的性能满足特定的要求。本节将讨论滤波器设计的基本要求,以及群延迟和相位失真的影响。
#### 2.3.1 滤波器设计的基本要求
滤波器设计时应考虑以下基本要求:
- **截止频率的精确度**:设计时要确保滤波器的截止频率符合预期值。
- **插入损耗**:这是信号通过滤波器时的功率损耗,理想情况下应尽可能小。
- **带宽**:滤波器允许信号通过的频率范围。
- **衰减**:截止频率之后的信号衰减量,应足够阻止不需要的频率成分。
- **带外抑制**:确保在截止频率外的信号被充分抑制,以避免干扰。
#### 2.3.2 群延迟与相位失真的影响
群延迟指的是不同频率成分的信号通过滤波器所需时间的差异。理想的低通滤波器应具有恒定的群延迟,即所有频率成分的信号都应以相同速度通过。如果群延迟随着频率变化,将会引起信号的相位失真,从而影响信号质量。
群延迟 \( \tau_g \) 可以通过传递函数 \( H(s) \) 的相位响应 \( \phi(\omega) \) 来计算:
\[ \tau_g(\omega) = -\frac{d\phi(\omega)}{d\omega} \]
设计滤波器时,确保滤波器在通带内具有平坦的群延迟是至关重要的,尤其是在无线通信中的基带信号处理中。
接下来,我们将深入探讨低通滤波器的具体设计与实现方法,以及它们在无线通信系统中的具体应用。
# 3. 低通滤波器的设计与实现
在无线通信中,低通滤波器(LPF)扮演着至关重要的角色,它可以允许低频信号通过,同时阻止高频信号。本章将详细讨论低通滤波器的设计与实现过程,包括模拟与数字滤波器的区分、实际设计案例分析以及性能评
0
0





