消费电子创新应用：低通滤波器设计趋势与案例分析


# 摘要
低通滤波器是信号处理中不可或缺的组件，用于去除信号中的高频噪声。本文全面概述了低通滤波器的理论基础，包括其定义、功能和关键参数。文中探讨了模拟与数字低通滤波器的设计理论，分析了各种设计工具的使用和实践，以及硬件实现的性能评估。此外，还深入研究了低通滤波器在消费电子、音频处理、电源管理和射频通信等领域的应用。本文还探讨了低通滤波器设计的创新趋势，包括集成电路技术的融合和智能算法的应用，并展望了未来技术，特别是物联网对低通滤波器设计的潜在影响。最后，通过案例研究和实验结果的分析，本文提供了对低通滤波器设计的深入理解及其在实际应用中的表现和优化途径。

# 关键字
低通滤波器；信号处理；设计理论；硬件实现；消费电子；智能算法；物联网；性能评估

参考资源链接：[PSIM仿真结果分析：FFT数据导出与Excel处理](https://wenku.csdn.net/doc/7on276eskx?spm=1055.2635.3001.10343)
# 1. 低通滤波器概述

低通滤波器（Low-Pass Filter，简称LPF）是一种允许低于截止频率的信号通过，同时削弱高于截止频率信号的电子设备。在信号处理领域，低通滤波器起着至关重要的作用，它能够清除高频噪声，保护电路免受高频干扰，确保信号的纯净和稳定。设计一个高效低通滤波器不仅仅依赖于硬件，更涉及到电路设计的理论知识和实际应用场景。

低通滤波器在各种电子设备中的应用广泛，从基本的音频设备到复杂的通信系统都有其身影。正确设计与使用低通滤波器，不仅可以提升电子产品的性能，还能延长其使用寿命。接下来的章节中，我们将详细探讨低通滤波器的理论基础，设计方法，以及在消费电子中的应用，帮助读者全面理解低通滤波器的设计与优化过程。

# 2. 低通滤波器的理论基础

### 2.1 低通滤波器的基本概念

#### 2.1.1 滤波器的定义与功能
滤波器是一种可以传递特定频率范围内的信号，同时抑制其他频率范围信号的电子电路或算法。它的功能是去除噪声，提升信号质量，以及实现信号的频谱选择。在信号处理中，滤波器根据其频率响应可以分为低通、高通、带通和带阻等不同类型。

在低通滤波器（LPF）的情况下，其主要功能是允许低于某一截止频率的信号分量通过，同时衰减高于该频率的信号分量。这在许多应用中是非常重要的，比如在音频信号处理中去除高频噪声，或在无线通信中减少干扰。

#### 2.1.2 低通滤波器的关键参数
低通滤波器的关键参数包括：
- 截止频率（fc）：定义为滤波器开始显著衰减信号的频率点。
- 通带（Passband）：在截止频率以下，信号几乎不受影响的频率范围。
- 阻带（Stopband）：在截止频率以上，信号显著衰减的频率范围。
- 过渡带宽度（Transition Band Width）：从通带的边缘到阻带的边缘的频率范围。
- 衰减（Attenuation）：指在阻带中信号幅度减少的量度，通常以分贝（dB）来度量。
- 相位响应（Phase Response）：滤波器对信号相位的影响，不同的滤波器设计会导致不同程度的相位失真。

### 2.2 模拟低通滤波器设计理论

#### 2.2.1 一阶与二阶低通滤波器设计
模拟低通滤波器的设计通常从基础的RC电路开始，这是一种一阶低通滤波器，包含一个电阻和一个电容。其截止频率由以下公式给出：
\[ f_c = \frac{1}{2\pi RC} \]
其中 \( f_c \) 是截止频率，\( R \) 是电阻值，\( C \) 是电容值。

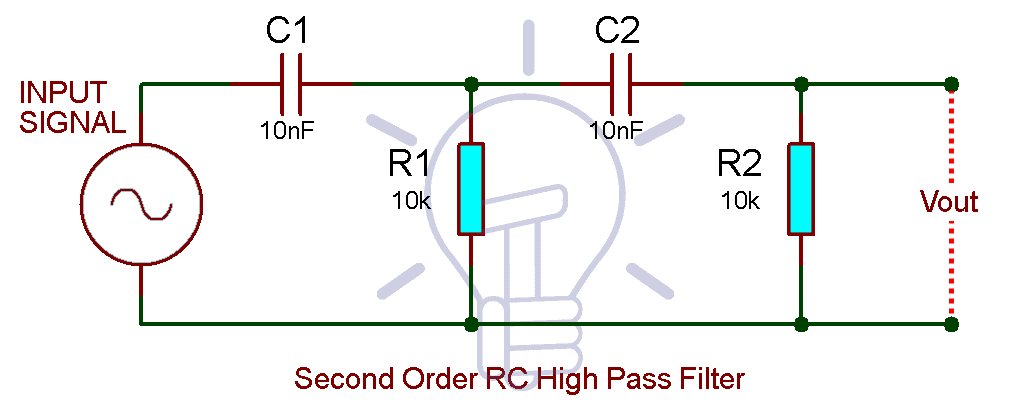
二阶低通滤波器通常使用两个RC网络或一个电感与一个RC网络的组合来构建。二阶滤波器相比一阶滤波器提供了更陡峭的滚降特性（roll-off），意味着信号在截止频率点附近的衰减速率更快。

#### 2.2.2 高阶低通滤波器的合成方法
高阶低通滤波器通常通过级联多个一阶或二阶滤波器来实现。级联方式允许设计者通过增加阶数来获得更陡峭的滚降特性，并更精确地定义通带和阻带的特性。高阶滤波器的设计可以通过巴特沃斯、切比雪夫、贝塞尔等多种逼近方法来实现不同的设计规格和性能。

### 2.3 数字低通滤波器设计理论

#### 2.3.1 离散时间信号处理基础
数字低通滤波器的基础是离散时间信号处理。与模拟滤波器不同，数字滤波器处理的是数字信号，即一系列离散时间点上的数值。设计数字低通滤波器需要考虑其在时域和频域内的行为。数字滤波器的设计往往首先在Z域内进行，然后通过数学变换转化为可实现的差分方程。

#### 2.3.2 数字滤波器的实现与设计
数字低通滤波器的实现可以通过FIR（有限冲击响应）和IIR（无限冲击响应）两种主要的滤波器结构。FIR滤波器通常具有线性相位特性，这使得它们在处理音频和图像信号时非常有用。IIR滤波器则通常有更高的效率和更小的计算负担，但其相位特性不如FIR滤波器线性。

数字滤波器的设计涉及到选择合适的滤波器类型、计算系数，以及确定滤波器的实现结构。设计者还需考虑稳定性、延迟、资源消耗和算法复杂度等因素。

为了指导设计数字滤波器，设计师通常会依赖于软件工具，如MATLAB，来执行滤波器系数的计算和验证滤波器性能。数字滤波器的设计过程通常涉及以下步骤：

1. 确定设计规格：包括通带截止频率、阻带截止频率、通带波纹和阻带衰减。
2. 选择滤波器类型：如巴特沃斯、切比雪夫、椭圆等。
3. 计算滤波器系数：可以手动计算，或使用专门的软件工具。
4. 实现滤波器：将系数应用于所选择的滤波器结构。
5. 测试和验证：使用测试信号来验证滤波器的实际性能是否满足设计规格。

# 示例代码：一个简单的FIR低通滤波器实现
def fir_lowpass_filter(input_signal, filter_coefficients):
    output_signal = []
    for sample in input_signal:
        output_signal.append(sum(sample * coefficient for sample, coefficient in zip(input_signal[-len(filter_coefficients):], filter_coefficients)))
    return output_signal

# filter_coefficients为预先计算好的滤波器系数
input_signal = [/* 一系列输入信号样本 */]
filtered_signal = fir_lowpass_filter(input_signal, filter_coefficients)

上述代码展示了如何通过预先计算好的滤波器系数来实现一个简单的FIR低通滤波器。每一步操作都有明确的数学和逻辑含义，计算结果可以用于进一步的信号分析或作为后续处理步骤的输入。

# 3. 低通滤波器设计工具与实践

## 3.1 模拟低通滤波器设计工具

### 3.1.1 滤波器设计软件介绍

在模拟低通滤波器的设计中，软件工具扮演着至关重要的角色。它们不仅简化了复杂的设计流程，还使得工程师能够在虚拟环境中测试和迭代设计。一个常用的滤波器设计软件是MATLAB，它提供了强大的工具箱，用于电路设计和仿真。MATLAB的Signal Processing Toolbox和Filter Design Toolbox是进行滤波器设计和分析的宝贵资源。此外，LTspice和Multisim也是流行的模拟仿真工具，它们提供了直观的电路设计和仿真界面，帮助工程师快速实现设计原型。

### 3.1.2 实际案例：模拟滤波器设计与仿真

通过一个实例，我们可以更清楚地看到模拟滤波器设计软件的应用。假设我们需要设计一个截止频率为1kHz的一阶RC低通滤波器。

1. 首先，在MATLAB中使用`butter`函数设计一个巴特沃斯滤波器。

   [b, a] = butter(1, 1000/(Fs/2), 'low');

这里`Fs`是采样频率，`1`表示一阶滤波器，`1000/(Fs/2)`确保了截止频率为1kHz。

2. 接下来，使用`freqz`函数来分析滤波器的频率响应。

   freqz(b, a);

这将显示一个图表，展示了滤波器的幅度和相位响应。

3. 最后，使用`filter`函数将设计好的滤波器应用到实际信号上。

   y = filter(b, a, x);

其中`x`是我们需要过滤的信号。

通过这样的设计流程，我们可以直接在软件中看到滤波器对信号的影响，并进行必要的调整，直到达到满意的效果。软件提供的仿真功能对于预测实际硬件行为至关重要，可以节省时间和成本，避免设计错误。

## 3.2 数字低通滤波器设计工具

### 3.2.1 数字信号处理软件应用

数字低通滤