【Origin FFT教程：频域与时域的桥梁】：深入理解FFT的奥秘


参考资源链接：[Origin入门详解：快速傅里叶变换与图表数据分析](https://wenku.csdn.net/doc/4ss1mdhfwo?spm=1055.2635.3001.10343)
# 1. 快速傅里叶变换(FFT)的基本原理

快速傅里叶变换（Fast Fourier Transform, FFT）是数字信号处理领域中一种高效的离散傅里叶变换（Discrete Fourier Transform, DFT）算法。在这一章中，我们将揭开FFT算法神秘的面纱，探讨其基础的理论与应用场景。

## 1.1 基本概念与定义

FFT是DFT的一种快速算法，它显著减少了计算DFT所需的复杂度。DFT将时域信号转换为频域信号，而FFT则以一种快速的方式执行这一转换。FFT算法的核心在于利用了DFT的对称性和周期性，通过分解和递归的方法，将原本需要O(N^2)的复杂度降低到O(NlogN)。

## 1.2 FFT的必要性

在数字信号处理中，频域分析是一种重要的技术手段。然而，直接计算DFT的高昂代价限制了其应用。FFT的出现解决了这一问题，使得在实际的工程与科学研究中，对信号进行快速频谱分析成为可能，极大地推动了技术的进步和创新。

## 1.3 本章小结

本章介绍了FFT的基本概念和必要性，为理解后续章节中FFT的深入理论与实践应用奠定了基础。在下一章，我们将详细探讨FFT的理论基础，包括时域与频域的概念、傅里叶变换的数学原理以及FFT算法的历史背景和意义。

# 2. FFT算法的理论基础

## 2.1 时域与频域的概念

### 2.1.1 时域信号分析
在时间域中，信号被看作随时间变化的量，其中数据点在时间轴上按顺序排列。时域分析允许我们观察和理解信号随时间的动态行为。例如，在电子学中，电路产生的电压或电流波形可以通过时域分析来描述。在音频处理中，声音波形作为随时间变化的气压波动，同样可以在时域上进行分析。

#### 信号的时域表示
信号的时域表示通常用函数s(t)表示，其中t代表时间变量。对于离散信号，这种表示转换为s[n]，其中n是整数索引。例如，一个简单的离散正弦波信号可以表示为：

s[n] = A \sin(2\pi f n + \phi)

这里，A代表幅度，f代表频率，而φ是初始相位。

在时域中，分析信号的特性包括：
- 振幅：信号的强度或高度。
- 相位：信号随时间的变化起点。
- 波形：信号的整体形状随时间变化。

### 2.1.2 频域信号分析
频域分析将信号分解为构成它的不同频率成分。在频域中，可以直观地看到各个频率分量对信号的贡献，这与在时域中观察信号随时间变化的形态大相径庭。频域分析在理解和处理信号特性方面提供了另一个重要的视角。

#### 频域表示与傅里叶变换
傅里叶变换是一种数学工具，它将时域信号转换为频域信号。在频域中，信号s(t)表示为一系列复数系数与不同频率正弦波的乘积，这一系列频率正弦波构成了傅里叶级数。

频域信号s(f)可以看作是时域信号s(t)的傅里叶变换：

s(f) = \int_{-\infty}^{\infty} s(t) e^{-j 2\pi f t} dt

此处，s(f)包含信号的幅度和相位信息，对应于每一个频率分量f。

在频域分析中，关注的特性包括：
- 频谱密度：表示不同频率分量的强度。
- 带宽：信号占据的频率范围。
- 谐波和噪声：信号中频率成分的纯净度。

时域与频域的分析提供了互补的信息，并且它们之间可以通过傅里叶变换相互转换。理解这两种域的分析方法是掌握FFT算法的关键。接下来，我们将深入探讨傅里叶变换的数学原理，以及离散傅里叶变换（DFT）和快速傅里叶变换（FFT）的概念。

# 3. FFT算法的实践操作

## 3.1 FFT算法的编程实现

### 3.1.1 FFT的实现步骤

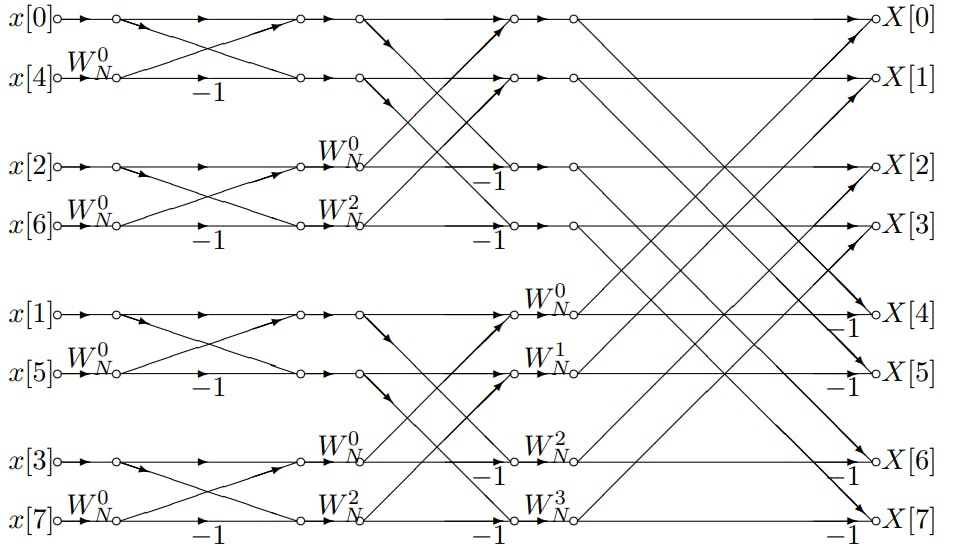
快速傅里叶变换（FFT）的实现步骤涉及将一个复杂的离散傅里叶变换分解成较小的DFT，这些步骤在多数情况下可并行处理，大大减少了计算量。FFT算法的步骤通常包括：

1. **分解数据**：将原始数据序列分解成偶数索引和奇数索引的数据序列。
2. **递归计算**：将分解得到的序列递归地应用FFT算法，直至每个序列足够小，可以直接计算其DFT。
3. **合并结果**：从递归计算得到的DFT结果中，合并得到最终的FFT结果。

实现FFT的一个关键点是利用了DFT的周期性和对称性，即DFT的系数是周期为N的复数，并且具有共轭对称性。这能够使我们在不增加计算量的情况下，复用已计算的结果。

### 3.1.2 实际代码案例分析

假设我们有以下Python代码片段，使用了`numpy`库中的`fft`函数来实现FFT：

import numpy as np

# 假设我们有一组时域信号
t = np.linspace(0, 1, 500, endpoint=False)
signal = np.sin(2 * np.pi * 5 * t) + 0.5 * np.sin(2 * np.pi * 12 * t)

# 对信号进行FFT变换
fft_result = np.fft.fft(signal)

# 获取FFT结果的频率分量
fft_freq = np.fft.fftfreq(len(signal), t[1]-t[0])

# 可视化原始信号和FFT变换后的频谱
import matplotlib.pyplot as plt

plt.figure(figsize=(12, 6))

plt.subplot(211)
plt.plot(t, signal)
plt.title('Original Signal')

plt.subplot(212)
plt.plot(fft_freq, np.abs(fft_result))
plt.title('FFT of the Signal')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')

plt.tight_layout()
plt.show()

上述代码段首先创建了一个由两个正弦波组成的时域信号。接着，使用`numpy.fft.fft`对信号进行快速傅里叶变换，并通过`numpy.fft.fftfreq`计算对应的频率分量。最后，使用`matplotlib`库绘制了原始信号和其频谱。

## 3.2 FFT在信号处理中的应用

### 3.2.1 频谱分析

频谱分析是FFT应用中最为广泛的一个方面。频谱分析通过将时域信号转换到频域，来识别信号中的频率成分。在FFT的频谱分析中，信号的频率内容被分解为一系列离散的频率分量，每个分量都有相应的幅度和相位。

### 3.2.2 信号滤波与压缩

FFT可用于信号的滤波和压缩，它允许直接操作信号的频域表示。信号中的噪声成分通常在频谱的特定区域表现出来，通过设置阈值去除或衰减这些区域的频率分量，可以实现有效的滤波。

例如，对音频信号进行低通滤波，可以去除高频噪声：

# 设定截止频率
cutoff_freq = 200  # 假设截止频率为200 Hz

# 对应于截止频率的索引
cutoff_index = int(cutoff_freq / (1.0 / len(signal)))

# 设置高频分量的幅度为0
fft_result[:cuto