【Origin FFT：可视化频域分析】：图形化技术深度解析


参考资源链接：[Origin入门详解：快速傅里叶变换与图表数据分析](https://wenku.csdn.net/doc/4ss1mdhfwo?spm=1055.2635.3001.10343)
# 1. 频域分析与FFT基本原理

频域分析是将信号从时域转换到频域中去研究的一种方法，在工程、物理、生物医学等领域广泛应用。在频域中，信号的特性如频率、相位和幅度可以更清晰地展现出来，为信号处理提供了更深入的洞察。快速傅里叶变换（FFT）是频域分析中最核心的算法之一，它将复杂的离散傅里叶变换（DFT）运算简化为更加高效的计算过程。

## 1.1 频域分析的重要性与应用领域

频域分析的重要性在于它能够提供对信号频率特性的深入理解。例如，在音频处理中，频域分析可以帮助我们区分不同音调的声音；在通信领域，它有助于分析信号的质量并优化传输效率；而在图像处理中，频域分析则可以用于压缩和细节增强。总之，频域分析在信号和图像处理、机械振动分析、生物医学工程以及许多其他技术领域中都有着广泛的应用。

## 1.2 快速傅里叶变换(FFT)数学原理

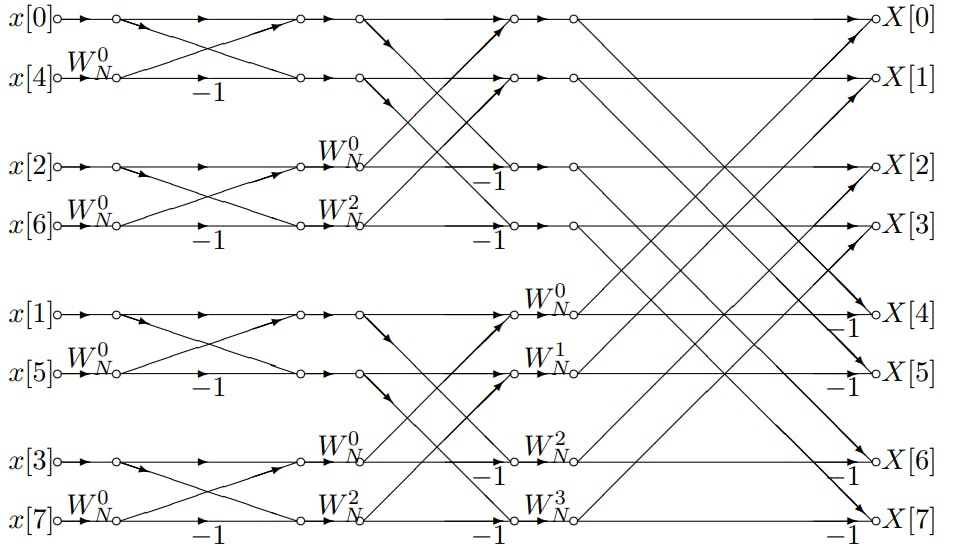
快速傅里叶变换是一种实现离散傅里叶变换(DFT)的算法，它能够将时域中的信号转换为频域信号。相比直接计算DFT，FFT算法极大地减少了计算量，使得复杂度从O(N^2)降低到O(NlogN)，其中N是信号样本数量。FFT算法的核心思想是通过分解DFT以利用对称性和周期性简化计算。这使得在实际应用中，FFT成为分析信号频率成分的实用工具。

# 2. Origin软件与FFT工具介绍

## 2.1 Origin软件概述

Origin是由OriginLab公司开发的一款科学绘图和数据分析软件，广泛应用于工程师、科研人员、学生等领域。它支持多种数据输入格式，可以进行复杂的统计分析，也提供了直观的界面进行数据可视化。

Origin的主要特点包括：
- 多样化的数据导入方式，支持Excel、文本文件、数据库等多种数据源。
- 强大的数据分析功能，包括信号处理、统计分析、非线性拟合等。
- 丰富的图形类型和定制选项，用户可以根据需要创建各类专业图表。
- 内置编程功能，可以使用LabTalk、Origin C等语言进行自动化任务。

## 2.2 Origin FFT工具的特色

Origin软件中的FFT工具是其信号处理模块的一部分，专为频域分析设计。这个工具具有以下几个特色：

- 用户友好：Origin FFT界面简洁明了，对新手友好，易于上手。
- 功能强大：支持单通道或多通道数据，可进行频谱分析、功率谱密度估计等。
- 参数可调：用户可以根据具体需求调整FFT参数，例如窗口类型、采样频率、长度等。
- 结果可视化：分析结果以图形方式展现，支持输出高质量的矢量图形。

## 2.3 Origin FFT与其它软件比较

虽然市场上存在多种可以进行FFT分析的软件，如Matlab、GNU Octave等，但Origin FFT有其独特的优势：

- 界面与操作简便：Origin设计有专门的向导模式，让分析过程更加直观。
- 高度集成：Origin提供的是一站式解决方案，无需额外转换数据即可进行后续分析。
- 数据管理：Origin对数据文件的管理更加高效，易于长期跟踪和分析。

接下来，我们将详细介绍Origin FFT的理论基础和操作流程。

# 3. Origin FFT的理论基础与操作流程

## 3.1 Origin FFT的理论基础

### 3.1.1 频域分析的重要性与应用领域

频域分析是研究信号频率成分的一种分析方法，它将时域中的信号转换为频域中的频率成分。这种分析方法在许多领域都有广泛的应用，例如通信、图像处理、声音分析等。频域分析可以帮助我们更好地理解信号的本质特征，比如信号的频率分布、能量分布等。通过频域分析，我们可以对信号进行滤波、压缩、增强等各种处理，以满足不同的应用需求。

频域分析的重要性还体现在其对信号特征的精确把握。在通信领域，频域分析可以帮助我们设计合适的调制解调方案，提高信号传输的效率和可靠性。在图像处理领域，频域分析可以用来进行图像压缩、边缘检测等操作。在声音分析领域，频域分析可以用来进行声音信号的增强、噪声抑制等处理。

### 3.1.2 快速傅里叶变换(FFT)数学原理

快速傅里叶变换（Fast Fourier Transform，FFT）是频域分析中的一种高效算法。它的基本思想是将长序列的离散傅里叶变换（DFT）分解为短序列的DFT，从而减少计算量。FFT算法的基本步骤是将信号分组，每组包含相等数量的数据点，然后对每组进行DFT操作。最终将所有组的DFT结果进行适当的组合，得到整个信号的频域表示。

FFT算法相较于传统的DFT算法，在计算复杂度上有着显著的优势。FFT算法的时间复杂度为O(NlogN)，而DFT的时间复杂度为O(N^2)，其中N为信号的长度。这种计算效率的提升使得FFT算法在工程实践和科研领域得到了广泛的应用。

## 3.2 Origin FFT的操作步骤

### 3.2.1 数据准备与导入

在进行Origin FFT分析之前，首先需要准备数据，并将其导入Origin软件中。Origin支持多种数据格式，包括文本文件、Excel文件等。数据通常以列的形式组织，其中一列是时间或位置信息，另一列是对应的信号数据。

导入数据到Origin中，可以使用菜单栏中的“File”->“Import”->“Excel”命令来导入Excel文件，或使用“File”->“Import”->“Text/CSV”命令来导入文本文件。导入时，需要确保数据的格式正确，并且列标题和数据类型符合要求。

### 3.2.2 FFT分析的操作流程与参数设置

导入数据之后，就可以进行FFT分析了。在Origin中进行FFT分析的基本步骤如下：

1. 选择需要分析的数据列。
2. 点击菜单栏中的“Analysis”->“Signal Processing”->“FFT”命令。
3. 在弹出的对话框中，根据需要设置FFT分析的参数。
4. 点击“OK”按钮，Origin将执行FFT分析，并显示结果。

在FFT分析的参数设置中，可以调整的参数包括：是否使用窗函数、窗函数的类型、是否进行双侧频谱分析、归一化的选择等。窗函数的作用是为了减少频谱泄露，常用窗函数包括矩形窗、汉宁窗、汉明窗等。双侧频谱分析是为了同时获得正频率和负频率的结果，通常用于需要分析信号相位信息的场合。

### 3.2.3 结果解读与常见问题处理

FFT分析完成后，Origin会生成相应的频域分析结果，并将其以图形的形式展现。解读FFT结果，需要关注的主要有幅度谱和相位谱。幅度谱显示了信号各个频率成分的强度，而相位谱则显示了这些频率成分的相位信息。

在解读FFT结果时，可能会遇到一些常见问题。例如，频谱中可能会出现频率泄漏，这是由于数据长度不足或窗函数选择不当造成的。解决这个问题，可以通过增加数据长度或更换窗函数来尝试解决。

另外，当进行双侧频谱分析时，可能会对结果产生误解。由于FFT结果是对称的，实际上只需要关注一半的频谱数据即可。对于这些常见问题，需要根据具体情况进行分析和处理。

## 表格：FFT参数设置选项说明

| 参数选项 | 说明 |
| ---------------- | ------------------------------------------------------------ |
| 使用窗函数 | 是否在FFT分析前对数据应用窗函数，以减少频谱泄露。 |
| 窗函数类型选择 | 提供多种窗函数，如矩形窗、汉宁窗、汉明窗等，供用户根据信号特性选择。 |
| 双侧频谱分析选项 | 选择是否进行双侧