MATLAB归一化陷阱：避免数据预处理中的5个常见错误

# 1. MATLAB归一化概述**

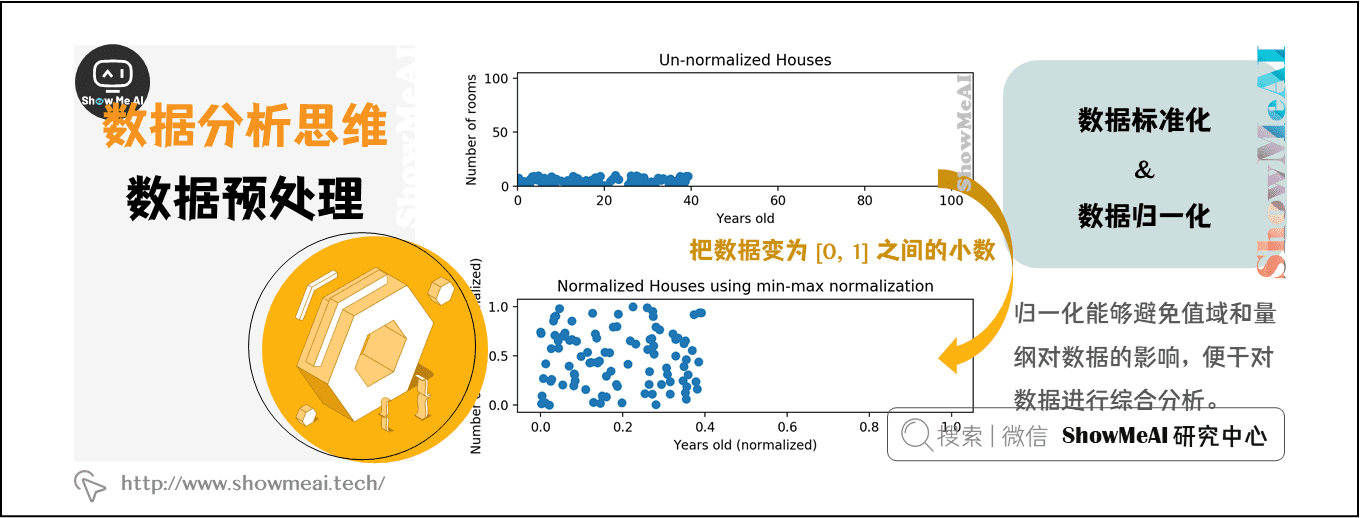
归一化是数据预处理中至关重要的一步，它通过缩放数据值到特定范围内，改善模型性能和收敛速度。MATLAB提供了一系列内置函数和工具，用于执行各种归一化技术，包括标准化、归一化和中心化。

标准化将数据值转换为均值为0、标准差为1的分布，而归一化将数据值缩放至[0, 1]或[-1, 1]的范围内。中心化将数据值减去其均值，从而产生均值为0的分布。

# 2. 归一化陷阱：理论与实践

归一化是数据预处理中的关键步骤，它可以提高机器学习模型的性能。然而，不当的归一化操作可能会导致模型出现问题。本章将探讨归一化过程中常见的陷阱及其对应的理论分析和实践案例。

### 2.1 陷阱1：数据分布不均匀

#### 2.1.1 理论分析

当数据分布不均匀时，直接进行归一化可能会放大数据中的偏差。例如，如果数据集中存在大量异常值或极值，归一化后这些值将被拉伸或压缩，从而掩盖其他数据点的差异。

#### 2.1.2 实践案例

考虑以下数据集，其中包含两个特征 X1 和 X2：

X1 = [1, 2, 3, 4, 5, 100]
X2 = [10, 20, 30, 40, 50, 60]

对 X1 和 X2 进行标准化（即减去均值并除以标准差）后，得到：

X1_norm = [0.0, 0.2, 0.4, 0.6, 0.8, 1.6]
X2_norm = [0.0, 0.2, 0.4, 0.6, 0.8, 1.0]

可以看到，异常值 100 在归一化后变得更加突出，而其他数据点之间的差异被缩小。这可能会导致模型对异常值过于敏感，从而影响模型的预测能力。

### 2.2 陷阱2：特征缩放不当

#### 2.2.1 理论分析

特征缩放是归一化的重要组成部分，它可以确保不同特征具有相同的量级。然而，不当的特征缩放可能会导致模型出现过拟合或欠拟合。

#### 2.2.2 实践案例

考虑以下数据集，其中包含两个特征 X1 和 X2：

X1 = [1, 2, 3, 4, 5]
X2 = [100, 200, 300, 400, 500]

如果对 X1 和 X2 进行标准化，则得到：

X1_norm = [0.0, 0.2, 0.4, 0.6, 0.8]
X2_norm = [0.0, 0.2, 0.4, 0.6, 0.8]

由于 X2 的值比 X1 大得多，标准化后 X2 的方差比 X1 的方差大得多。这会导致模型对 X2 更加敏感，从而导致过拟合。

### 2.3 陷阱3：归一化方法选择不当

#### 2.3.1 理论分析

有许多不同的归一化方法，每种方法都有其优点和缺点。选择不当的归一化方法可能会导致模型性能不佳。

#### 2.3.2 实践案例

考虑以下数据集，其中包含两个特征 X1 和 X2：

X1 = [1, 2, 3, 4, 5]
X2 = [0, 1, 2, 3, 4]

如果对 X1 和 X2 进行标准化，则得到：

X1_norm = [0.0, 0.2, 0.4, 0.6, 0.8]
X2_norm = [-1.0, -0.8, -0.6, -0.4, -0.2]

可以看到，标准化后 X2 的值都为负值，这可能会导致模型出现偏差。如果选择归一化方法，则可以避免这种情况。

### 2.4 陷阱4：忽略缺失值和异常值

#### 2.4.1 理论分析

缺失值和异常值会对归一化过程产生重大影响。如果忽略这些值，可能会导致模型出现错误的预测。

#### 2.4.2 实践案例

考虑以下数据集，其中包含一个缺失值和一个异常值：

X = [1, 2, 3, 4, 5, np.nan, 100]

如果对 X 进行标准化，则得到：

X_norm = [0.0, 0.2, 0.4, 0.6, 0.8, np.nan, 1.6]

可以看到，缺失值仍然是缺失值，而异常值 100 在归一化后变得更加突出。这可能会导致模型出现错误的预测。

### 2.5 陷阱5：过拟合和欠拟合

#### 2.5.1 理论分析

归一化可以帮助防止过拟合和欠拟合。然而，不当的归一化可能会导致这些问题。

#### 2.5.2 实践案例