Ansys非线性分析求解器：选择与设置的独家秘籍


# 摘要
本文系统介绍了非线性分析的基本概念、Ansys非线性求解器的理论基础、求解器的选择与设置以及非线性分析在实践中的应用案例。文章首先阐述了非线性分析的分类及其理论，随后详细解释了Ansys求解器的算法原理，包括不同非线性问题求解的策略。在实践应用章节中，本文提供了多个案例，覆盖了材料非线性、接触问题以及多物理场耦合的分析。最后，文章探讨了非线性分析的挑战和未来发展趋势，特别是多尺度问题的处理与人工智能在非线性分析优化方面的应用潜力。

# 关键字
非线性分析；Ansys求解器；理论基础；实践应用；材料非线性；多物理场耦合

参考资源链接：[ANSYS非线性分析详解：几何与材料非线性，案例与注意事项](https://wenku.csdn.net/doc/sy6713p7s2?spm=1055.2635.3001.10343)
# 1. 非线性分析的基本概念

在现代工程设计中，非线性分析已经成为理解和解决复杂工程问题不可或缺的工具。非线性分析关注的是在加载过程中，材料、结构或边界条件表现出的非线性行为，它与线性分析的本质区别在于，其关系不能用简单的线性方程来描述。本章将介绍非线性分析的核心理念和基础知识，为后面章节中具体的Ansys软件操作和案例分析打下坚实的基础。通过学习本章内容，读者将能够理解非线性效应的来源，以及非线性分析在工程中的重要性和应用范围。

# 2. Ansys非线性求解器的理论基础

### 2.1 非线性分析的分类和理论

#### 2.1.1 静态非线性与动态非线性分析

在非线性分析的分类中，静态非线性分析通常关注在静态载荷下的材料和结构响应，如材料的屈服、硬化和软化现象。这类分析常用于研究桥梁、建筑结构以及机械零件在长期荷载作用下的变形和破坏。静态非线性问题的求解不考虑惯性和阻尼效应，其核心在于分析材料的非线性应力-应变关系以及由结构大变形引起的几何非线性效应。

另一方面，动态非线性分析则是处理包含惯性和阻尼效应的非线性问题，如冲击、振动和爆炸等动态事件。动态分析通常需要更复杂的数学模型和更多的计算资源。在动态非线性分析中，除了要处理静态非线性分析中涉及的所有非线性因素外，还需考虑时间效应以及结构随时间变化的动态响应。

#### 2.1.2 材料非线性、几何非线性与边界条件非线性

在非线性分析中，非线性的来源可以是材料行为、几何形状变化或是边界条件的变化。材料非线性通常指材料应力-应变关系中的非线性行为，如弹塑性材料的硬化或软化，以及非线性弹性材料和粘塑性材料的行为。几何非线性分析则关注在载荷作用下结构的形状变化，如大位移、大转动或大应变问题，这些变形可能会导致结构刚度的显著变化。边界条件非线性指的是由于边界条件的改变导致结构响应的非线性，例如支撑的移动、接触问题中的非线性边界。

### 2.2 Ansys非线性求解器的算法原理

#### 2.2.1 牛顿-拉夫森方法与修正的弧长方法

牛顿-拉夫森方法（Newton-Raphson method）是求解非线性方程的一种迭代技术，它依赖于雅可比矩阵（或称为切线刚度矩阵）来预测系统的下一步状态。在Ansys中，牛顿-拉夫森方法用于迭代求解非线性平衡方程，每一步都需要重新线性化和求解雅可比矩阵，然后通过更新位移增量来逼近真实解。

修正的弧长方法（Modified Arc Length Method）是一种用于解决求解过程发散问题的策略，当系统响应难以通过传统的迭代方法跟踪时，它可以帮助找到解的路径。该方法通过引入一个额外的弧长参数，为非线性求解提供更多的方向性信息，从而允许系统在跨越载荷-位移路径上的某些不连续性或不稳定点时继续收敛。

#### 2.2.2 拟牛顿法和子空间迭代法

拟牛顿法（Quasi-Newton Methods）是牛顿-拉夫森方法的一种改进形式，用于减少每次迭代中雅可比矩阵求逆的计算量。这类方法通过更新一个近似的逆矩阵或近似的切线刚度矩阵，来逼近真实的雅可比矩阵，从而减少计算成本。BFGS（Broyden-Fletcher-Goldfarb-Shanno）和DFP（Davidon-Fletcher-Powell）是两种常用的拟牛顿法。

子空间迭代法（Subspace Iteration Method）是一种用于求解大型特征值问题的技术，它特别适用于求解结构动力学问题中的模态分析。该方法通过在子空间中进行迭代，有效地减少计算工作量，并使得求解过程更加高效。

#### 2.2.3 非线性方程组求解的策略

非线性方程组求解是一个复杂的过程，通常需要结合多种技术来确保收敛性。对于大规模非线性问题，Ansys提供了多种求解策略，例如自适应下降法（Adaptive Descent Method）和阻尼技术。自适应下降法通过动态调整下降方向和步长来避免系统发散，而阻尼技术则通过引入人为的阻尼因子来控制解的稳定性，从而提高收敛速度。

### 2.3 非线性分析中的一些关键概念

#### 2.3.1 刚度矩阵与载荷增量

在结构分析中，刚度矩阵描述了结构的刚度特性，它反映了在单位载荷作用下结构各部分产生的位移。非线性分析中的刚度矩阵需要考虑材料非线性、几何非线性和边界条件的非线性影响。因此，刚度矩阵是随位移变化而变化的，称为切线刚度矩阵。

载荷增量是指在求解非线性问题时，对载荷逐步施加的过程。将载荷分成多个增量步进行分析，有助于控制计算的稳定性和收敛性。每一步增量结束后，结构的响应被更新，然后用新的平衡状态作为下一步增量的起点。

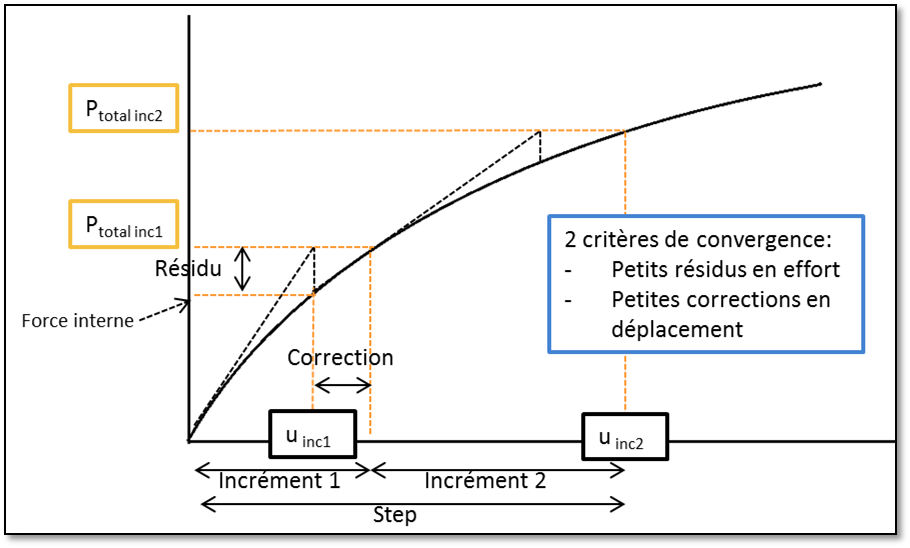
#### 2.3.2 收敛标准与平衡迭代

收敛标准是判断非线性求解是否达到可接受精度的条件。在Ansys中，常用的收敛标准包括位移收敛、力收敛和能量收敛等。位移收敛关注节点位移的变化量，力收敛则检查节点力或内力是否