图论精讲：visit算法在图数据结构中的核心作用

# 1. 图论基础知识与术语

图论是研究图的数学理论和应用的学科，它在计算机科学、网络分析、调度理论等领域拥有广泛应用。图由顶点（节点）和边组成，能够形象地表示物体之间的复杂关系。

## 1.1 图的定义和组成部分

图（Graph）G可定义为一个二元组(G, E)，其中G是顶点集，E是边集。边是连接两个顶点的线段，可以是有向或无向的，这决定了图的类型。

## 1.2 图的类型和特性

根据边的特性，图可以分为有向图（Digraph）和无向图。有向图的边具有方向，表示为<vi, vj>；无向图的边无方向，表示为(vi, vj)。特性主要表现在连通性、环、度数等方面，这些都会影响图的处理方法和算法设计。

# 2. 图的数据表示方法

### 2.1 图的基本概念

#### 2.1.1 图的定义和组成部分

图是一种数据结构，用于表示事物之间的关系。在图论中，图由一组顶点（vertices）和连接这些顶点的边（edges）组成。顶点通常用数字、字母或其他标识符表示，而边表示顶点之间的某种关系。图可以是有向的（由箭头表示边的方向）或无向的（边表示两个顶点之间有关系但没有方向）。顶点的度（degree）是指与该顶点相连的边的数量，对于有向图，度分为入度（in-degree）和出度（out-degree），分别表示进入和离开该顶点的边的数量。

#### 2.1.2 图的类型和特性

图的类型主要分为无向图和有向图，以及加权图和非加权图。在加权图中，每条边都有一个权重（weight），通常用于表示成本、距离或时间等度量。图的特性包括连通性、完全图、子图、平面图等。连通图是指从任意顶点出发，可以到达图中的所有其他顶点。完全图是一种特殊形式的图，其中每对不同的顶点都由一条边直接相连。图的子图是由原图的部分顶点和边构成的图。

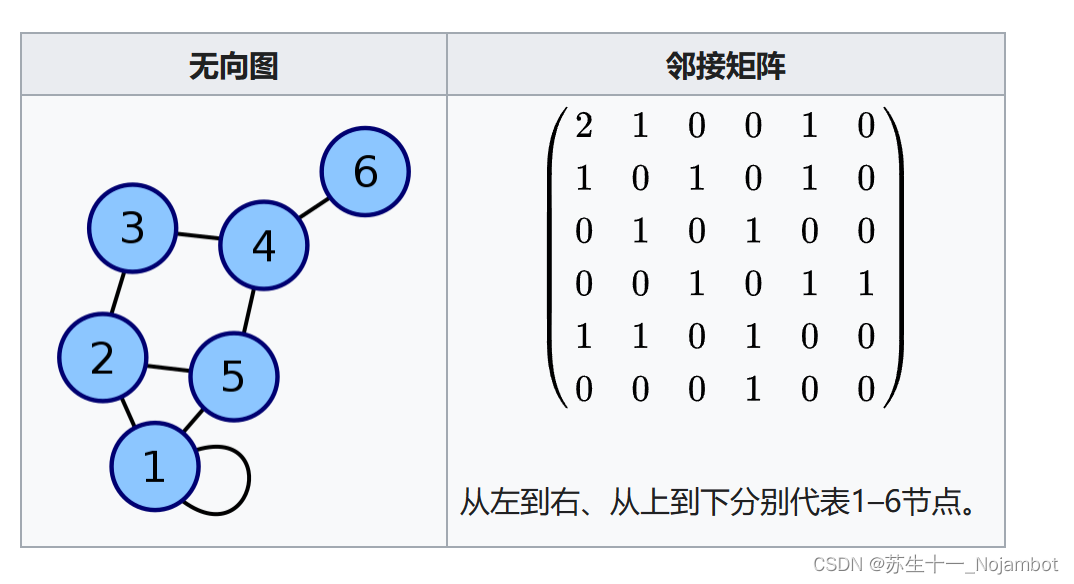
### 2.2 图的邻接矩阵表示

#### 2.2.1 邻接矩阵的定义和性质

邻接矩阵是一个二维数组，用来表示图中顶点之间的邻接关系。对于无向图，邻接矩阵是对称的；而对于有向图，则不一定是。矩阵的元素通常用0和1来表示，其中1表示两个顶点之间有边相连，而0表示没有。邻接矩阵的主要性质是其反映了图的稠密性，即边的数量与顶点数的平方成正比时，邻接矩阵是稠密的。

#### 2.2.2 邻接矩阵在图操作中的应用

邻接矩阵在图的操作中非常方便，尤其是进行图的遍历（如DFS和BFS）时，只需简单地检查邻接矩阵即可得知是否有边连接顶点。它也便于执行图的基本操作，如添加或删除边。然而，邻接矩阵的缺点是空间复杂度高，尤其在稀疏图中会导致大量的内存浪费。

### 2.3 图的邻接表表示

#### 2.3.1 邻接表的构建和特点

邻接表是图的另一种常见表示方法，它比邻接矩阵更节省空间，尤其是在表示稀疏图时。邻接表是一个数组，数组的每个元素是一个链表或列表，链表中包含了与该顶点相连的所有顶点。因此，顶点的邻接表实际上表示了从该顶点出发可以到达的所有顶点。邻接表的特点是空间复杂度低，操作灵活。

#### 2.3.2 邻接表在图搜索中的效率分析

在图的搜索操作中，如DFS和BFS，邻接表可以提供比邻接矩阵更高的效率。由于邻接表不需要遍历整个顶点集，而是直接访问与当前顶点相连的邻接顶点，因此可以减少不必要的计算。在进行图的搜索时，邻接表结构提供了快速跳转到邻接顶点的能力，这对于优化搜索过程至关重要。

graph LR
A[邻接矩阵] -->|边多空间大| B[适用于稠密图]
A -->|边少空间浪费| C[邻接表]
C -->|边少空间省| D[适用于稀疏图]
D -->|搜索效率高| E[DFS和BFS]

#### 邻接表伪代码示例

# 邻接表的Python实现
class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.adj_list = [[] for _ in range(vertices)]

    def add_edge(self, src, dest):
        self.adj_list[src].append(dest)  # 在src顶点的邻接表中添加dest
        # 有向图需要单独处理，无向图此处添加即可

# 使用邻接表构建图并添加边
g = Graph(4)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(2, 3)
g.add_edge(3, 3)

在这个伪代码示例中，我们首先创建了一个图对象`Graph`，它包含一个顶点列表`adj_list`。该列表的每个索引对应图中的一个顶点，每个索引位置上的列表存储了与该顶点相邻的顶点。例如，`g.add_edge(0, 1)`表示顶点0和顶点1相邻。

#### 邻接矩阵与邻接表的空间复杂度比较

- **邻接矩阵：** 空间复杂度为O(V^2)，其中V是顶点的数量。
- **邻接表：** 空间复杂度为O(V + E)，其中E是边的数量。

由于在稀疏图中，边的数量E通常远小于V^2，邻接表的空间复杂度往往显著低于邻接矩阵。对于稠密图，边的数量接近顶点数平方，此时邻接矩阵的空间使用相对较少，且由于其对称性，存储效率较高。

从实际应用的角度来看，选择合适的数据结构是优化性能的关键。在处理大规模数据时，邻接表通常是首选，因为它可以节省大量的内存资源，并且提供了高效的数据存取能力。然而，在某些特定情况下，如图非常稠密或需要频繁进行矩阵运算时，邻接矩阵可能更为适用。

# 3. visit算法详解

## 3.1 visit算法的核心原理

### 3.1.1 visit算法的定义和目的

visit算法是一类用于遍历或搜索图的节点的算法。其核心思想是确保每个节点仅被访问一次。这一过程经常用于数据结构中的图，尤其是在图的节点数量庞大或节点间关系复杂时。visit算法的目的在于：

1. **检索数据：** 在图中寻找特定的数据。
2. **分析结构：** 探索节点间的连接方式，如连通性检测。
3. **优化计算：** 通过访问顺序的选择来最小化搜索成本。

visit算法不仅限于搜索，在解决问题的过程中也可以用来检测循环依赖、进行路径查找等。

### 3.1.2 visit算法的算法流程

visit算法的一般流程包含以下步骤：

1. **初始化：** 选择起始节点，标记为已访问。
2. **递归或迭代：** 依据特定顺序访问相邻节点。
3. **回溯：** 在遇到死胡同时，返回上一个节点并继续探索其他路径。
4. **标记：** 记录访问过的节点，确保不重复访问。

visit算法的形式化伪代码可以表示为：

function visit(node):
    if node is visited:
        return
    mark node as visited
    perform some action, like printing node's value
    for each neighbor of node:
        if neighbor is not visited:
            visit(neighbor)

## 3.2 visit算法的变体

### 3.2.1 深度优先搜索（DFS）

深度优先搜索（DFS）是一种基于递归的visit算法变体。在DFS中，算法尽可能地深入每一个分支，直到无法进一步深入为止，然后回溯并继续探索下一个可能的分支。

#### 深度优先搜索的实现

# DFS 实现示例
def dfs(graph, start, visited=N