图遍历性能之谜：细数visit算法的效率与挑战

# 1. 图遍历算法的理论基础

图遍历是计算机科学中的一项基本技术，对于数据结构的深度理解和复杂网络分析至关重要。在这一章节中，我们将探讨图遍历的核心概念、数据结构以及算法的基础理论。

## 1.1 图的表示方法
在计算机科学中，图可以用两种主要的表示方法：邻接矩阵和邻接表。邻接矩阵是一种二维数组，用于表示节点之间的连接关系，适合稠密图。邻接表则是一种链表的集合，每个链表代表图中的一个节点及其相邻节点，更适合稀疏图。选择合适的图表示方法对于图遍历算法的性能具有显著影响。

## 1.2 遍历算法的基本类型
图遍历算法可以分为两大类：深度优先搜索（DFS）和广度优先搜索（BFS）。DFS通过尽可能深地搜索图的分支，直到达到叶子节点，然后再回溯。而BFS则从一个节点开始，逐层向外扩展，直到访问到所有可达节点。两者在实现时依赖于数据结构中的栈（DFS）和队列（BFS）。

## 1.3 遍历算法的重要性
图遍历算法不仅是解决实际问题的基石，如网络路由、社交网络分析和搜索引擎排名，而且还在计算机科学的许多其他领域发挥着关键作用。例如，图遍历在实现网络协议和优化搜索引擎排名中起到至关重要的作用。了解并掌握图遍历算法的原理和应用，对于任何希望深入理解算法和数据结构的IT专业人士来说都是必不可少的。

# 2. 深度优先搜索算法（DFS）

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。它从一个节点开始，尽可能深地搜索每个分支，直到满足特定条件。DFS通过使用栈或递归技术实现，并广泛应用于解决各种计算机科学问题。接下来，我们将深入探讨DFS的理论、实现以及在不同场景下的应用和优化策略。

## 2.1 DFS的理论与实现

### 2.1.1 DFS的算法原理

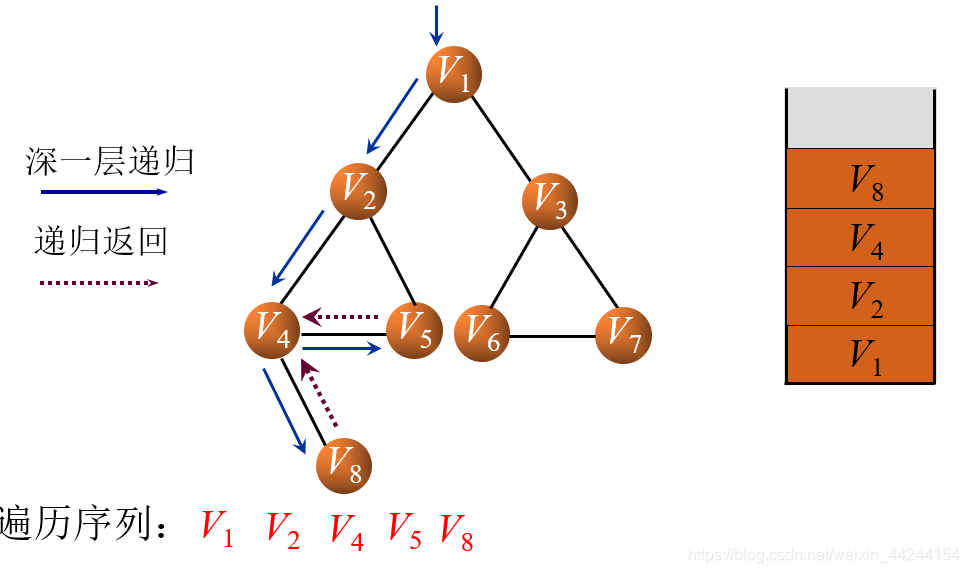
深度优先搜索是图遍历的一种方法，它沿着图的分支尽可能深地遍历，直到到达一个没有未访问的邻居的节点，然后回溯到上一个节点，继续探索其他分支。此算法可以利用递归或栈实现。

在递归实现中，DFS的函数会递归地对每一个未访问的邻居调用自身，直到该分支上没有更多节点可以访问。在使用栈的非递归实现中，算法会维护一个栈，用于存储接下来要访问的节点，同时使用一个集合记录已经访问过的节点。

### 2.1.2 DFS的时间复杂度分析

DFS的时间复杂度取决于图的实现方式。对于邻接矩阵表示的图，每次访问一个节点的邻居时都需要检查矩阵中的每一行，时间复杂度为O(V^2)，其中V是节点的数量。而使用邻接表表示图时，访问所有节点的邻居所需的时间与边的数量成正比，因此时间复杂度为O(V+E)。

## 2.2 DFS在有向图和无向图中的应用

### 2.2.1 有向图中的DFS算法实现

在有向图中，DFS用于检测图中是否存在从一个节点到另一个节点的路径、遍历所有可达节点、或检测图的连通分量。DFS遍历的顺序可能会受到有向图中边的方向影响。

有向图中的DFS实现与一般DFS类似，只是在选择下一个要访问的节点时，只考虑从当前节点出发的边的方向。例如，在解决网页爬取问题时，可以使用DFS来递归地访问网页中的链接。

def dfs_directed(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start)  # Process the node
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs_directed(graph, neighbor, visited)
    return visited

# Example usage:
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}
dfs_directed(graph, 'A')

### 2.2.2 无向图中的DFS算法实现

无向图的DFS实现与有向图类似，但是边的方向不影响访问的顺序。在无向图中，DFS常用于寻找连通分量、检测环、以及求解迷宫问题等。算法遍历每个节点一次，因此其时间复杂度为O(V+E)。

def dfs_undirected(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start)  # Process the node
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs_undirected(graph, neighbor, visited)
    return visited

# Example usage:
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}
dfs_undirected(graph, 'A')

## 2.3 DFS的优化策略

### 2.3.1 剪枝技术及其效果

在执行DFS时，剪枝技术可以显著提高效率，尤其是用于解决搜索问题时。剪枝通过提前终止某些分支的搜索，避免不必要的遍历。

例如，在解决迷宫问题时，如果我们希望找到一条从起点到终点的路径，一旦我们从当前分支找到了这样一条路径，就没有必要继续搜索其他分支，可以直接回溯到上一个节点。

### 2.3.2 记忆化搜索的应用

记忆化搜索是另一种优化DFS的技术，它利用一个记录结构（如字典或数组）来保存已经计算过的结果。在DFS递归调用前，先检查结果是否已经计算过，如果计算过则直接使用结果，否则继续计算并将结果存入记录结构。

记忆化搜索在解决带有重叠子问题的动态规划问题中非常有用。通过避免重复计算相同子问题，它可以显著降低时间复杂度。

以上内容涵盖了DFS的基本理论和实现，以及在有向图和无向图中应用DFS的示例代码和逻辑分析。下一章节将探讨广度优先搜索算法（BFS）的原理、实现以及它在图遍历中的应用。

# 3. 广度优先搜索算法（BFS）

## 3.1 BFS的理论与实现

### 3.1.1 BFS的算法原理

广度优先搜索算法（BFS）是一种用于图遍历或搜索树结构的算法，其核心思想是沿着树的宽度方向进行扩展，先访问所有的近邻节点，然后再逐渐深入访问更远的节点。BFS的这一特点使得它适合解决许多与最短路径或者最小跳数相关的问题。在树结构中，BFS类似于逐层剥洋葱的遍历方式。

算法从一个初始节点开始，首先访问该节点的所有邻接节点，并将这些邻接节点放入一个队列中。之后，BFS从队列中取出一个节点，并重复上述过程：访问该节点的所有未被访问过的邻接节点，并将这些节点加入队列。这个过程一直持续到队列为空为止。

### 3.1.2 BFS的时间复杂度分析

BFS的时间复杂度分析要基于图的表示方式。假设图G有V个顶点和E条边，BFS的时间复杂度是O(V+E)。这是因为算法从每一个顶点出发，遍历其所有邻接边。在这种情况下，每个顶点和每条边都会被访问一次，从而保证了时间效率。

在BFS的实现中，需要特别注意数据结构的选择。队列是BFS中不可或缺的组件，它负责存储待访问的节点。在Python中，我们可以使用`collections.deque`来实现一个高效双端队列。

## 3.2 BFS在图遍历中的应用

### 3.2.1 寻找最短路径

BFS能够用于在加权无向图中寻找两点之间的最短路径。当BFS从源节点开始执行时，它会首先找到距离源节点最近的所有节点，然后是次近的节点，依此类推。因此，一旦目标节点被访问，算法就可以停止，此时访问到目标节点的路径就是最短路径。

为了记录路径，可以使用一个前驱指针数组，该数组记录每个节点的前驱节点。最终，可以通过回溯这个数组来构建出最短路径。

from collections import deque

def bfs_shortest_path(graph, start, end):
    visited = set()
    queue = deque([start])
    parent = {start: None}  # Keep