单片机程序设计PID控制指南：深入理解原理与应用，让你的系统更稳定

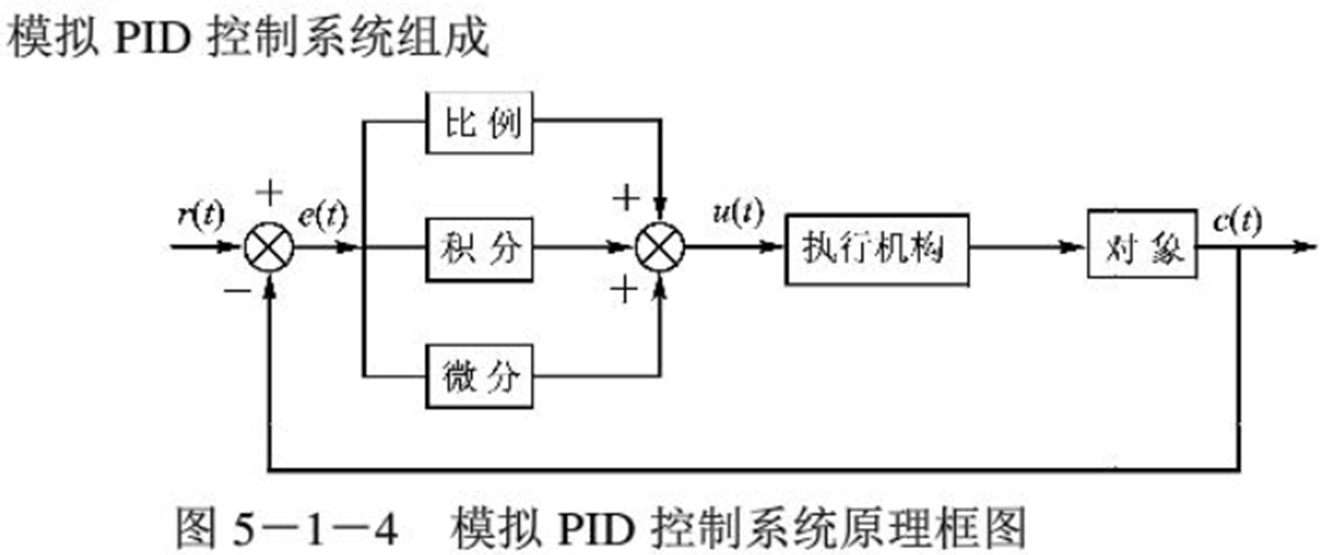
# 1. PID控制理论基础

PID控制（比例-积分-微分控制）是一种经典的反馈控制算法，广泛应用于各种工业自动化系统中。它通过测量系统输出与期望值之间的误差，并根据误差的比例、积分和微分值来调整控制输出，从而实现对系统的控制。

PID控制算法的数学原理如下：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* u(t) 为控制输出
* e(t) 为误差（期望值 - 输出值）
* Kp、Ki、Kd 为 PID 参数（比例、积分、微分增益）

# 2. PID控制算法实现

### 2.1 PID算法的数学原理

PID算法的全称为比例-积分-微分算法，是一种经典的反馈控制算法。其数学原理如下：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* `u(t)` 为控制器的输出
* `e(t)` 为误差，即目标值与实际值之差
* `Kp` 为比例系数
* `Ki` 为积分系数
* `Kd` 为微分系数

### 2.2 PID算法的实现方法

PID算法有三种实现方法：位置式、增量式和微分式。

#### 2.2.1 位置式PID算法

位置式PID算法的公式如下：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* `u(t)` 为控制器的输出
* `e(t)` 为误差，即目标值与实际值之差
* `Kp` 为比例系数
* `Ki` 为积分系数
* `Kd` 为微分系数

位置式PID算法的特点是：

* 响应快，但容易产生超调
* 积分项可以消除稳态误差
* 微分项可以提高系统的稳定性

#### 2.2.2 增量式PID算法

增量式PID算法的公式如下：

u(t) = u(t-1) + Kp * (e(t) - e(t-1)) + Ki * e(t) + Kd * (e(t) - 2 * e(t-1) + e(t-2))

其中：

* `u(t)` 为控制器的输出
* `u(t-1)` 为上一次控制器的输出
* `e(t)` 为误差，即目标值与实际值之差
* `Kp` 为比例系数
* `Ki` 为积分系数
* `Kd` 为微分系数

增量式PID算法的特点是：

* 响应慢，但不易产生超调
* 积分项可以消除稳态误差
* 微分项可以提高系统的稳定性

#### 2.2.3 微分式PID算法

微分式PID算法的公式如下：

u(t) = Kp * (e(t) - e(t-1)) + Ki * ∫e(t)dt + Kd * (e(t) - 2 * e(t-1) + e(t-2))

其中：

* `u(t)` 为控制器的输出
* `e(t)` 为误差，即目标值与实际值之差
* `Kp` 为比例系数
* `Ki` 为积分系数
* `Kd` 为微分系数

微分式PID算法的特点是：

* 响应快，但容易产生超调
* 积分项可以消除稳态误差
* 微分项可以提高系统的稳定性

### 2.3 PID参数整定方法

PID参数的整定对于PID控制器的性能至关重要。常用的PID参数整定方法有：

#### 2.3.1 Ziegler-Nichols方法

Ziegler-Nichols方法是一种基于系统阶跃响应的PID参数整定方法。其步骤如下：

1. 将PID控制器切换到P控制模式，即`Ki = Kd = 0`。
2. 逐渐增大比例系数`Kp`，直到系统出现持续振荡。
3. 记录此时`Kp`的值，记为`Kp_u`，和振荡周期，记为`T_u`。
4. 根据`Kp_u`和`T_u`，计算PID参数：

Kp = 0.6 * Kp_u
Ki = 2 * Kp / T_u
Kd = Kp * T_u / 8

#### 2.3.2 Cohen-Coon方法

Cohen-Coon方法也是一种基于系统阶跃响应的PID参数整定方法。其步骤如下：

1. 将PID控制器切换到P控制模式，即`Ki = Kd = 0`。
2. 逐渐增大比例系