单片机程序设计数据结构指南：掌握存储与组织数据，让你的程序更清晰

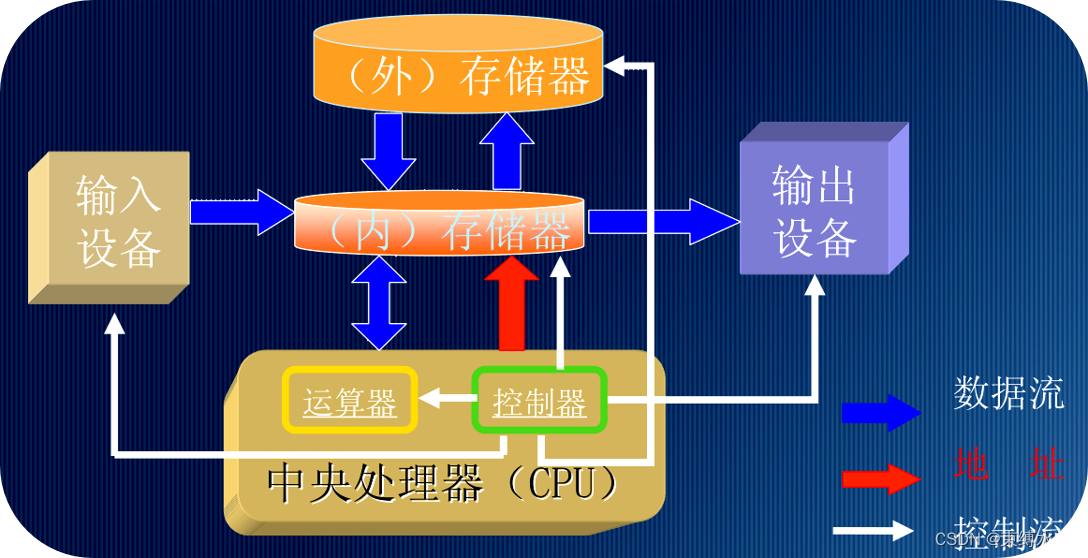
# 1. 单片机程序设计数据结构概述

数据结构是组织和管理数据的方式，在单片机程序设计中起着至关重要的作用。它决定了数据的存储、组织和检索效率。本章将概述数据结构的基本概念，包括其定义、分类、抽象和实现。此外，还将介绍数据结构的性能分析，包括时间复杂度和空间复杂度分析。

# 2. 数据结构理论基础

### 2.1 数据结构的基本概念和分类

#### 2.1.1 数据结构的定义和分类

**定义：**

数据结构是组织和存储数据的抽象方式，它定义了数据的逻辑关系和操作方式。

**分类：**

数据结构可分为以下几类：

- **线性结构：**数据元素按线性顺序排列，如数组、链表、栈、队列。
- **非线性结构：**数据元素之间存在非线性关系，如树、图。
- **其他结构：**哈希表、堆、集合等。

### 2.1.2 数据结构的抽象和实现

**抽象：**

数据结构的抽象是指定义数据结构的逻辑特性，而不考虑其具体实现方式。抽象层可以隐藏实现细节，便于数据结构的理解和使用。

**实现：**

数据结构的实现是指使用特定的编程语言或数据结构库来实现抽象的数据结构。实现层可以提供具体的数据存储和操作机制。

### 2.2 数据结构的性能分析

#### 2.2.1 时间复杂度分析

时间复杂度是指执行数据结构操作所需的时间。它通常用大 O 符号表示，如 O(n)、O(log n)、O(n^2)。

**常见的时间复杂度：**

| 操作 | 时间复杂度 |
|---|---|
| 查找 | O(n)、O(log n) |
| 插入 | O(1)、O(n) |
| 删除 | O(1)、O(n) |

#### 2.2.2 空间复杂度分析

空间复杂度是指存储数据结构所需的空间。它通常用大 O 符号表示，如 O(n)、O(log n)、O(n^2)。

**常见的空间复杂度：**

| 数据结构 | 空间复杂度 |
|---|---|
| 数组 | O(n) |
| 链表 | O(n) |
| 栈 | O(n) |
| 队列 | O(n) |

### 代码块示例：

# 数组的时间复杂度分析

def find_element(arr, element):
    for i in range(len(arr)):
        if arr[i] == element:
            return i
    return -1

# 时间复杂度：O(n)

**逻辑分析：**

该代码块实现了一个在数组中查找元素的函数。函数遍历数组中的每个元素，如果找到匹配的元素，则返回其索引。由于函数需要遍历整个数组，因此其时间复杂度为 O(n)。

### 表格示例：

| 数据结构 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 数组 | O(1) | O(n) |
| 链表 | O(n) | O(n) |
| 栈 | O(1) | O(n) |
| 队列 | O(1) | O(n) |
| 树 | O(log n) | O(n) |
| 图 | O(V + E) | O(V + E) |

**参数说明：**

- V：图中顶点的数量
- E：图中边的数量

### Mermaid 流程图示例：

graph LR
    subgraph 数据结构
        A[数组] --> B[链表]
        A[数组] --> C[栈]
        A[数组] --> D[队列]
        B[链表] --> C[栈]
        B[链表] --> D[队列]
        C[栈] --> D[队列]
    end

**流程图说明：**

该流程图展示了不同数据结构之间的关系。箭头表示数据结构之间的依赖关系或转换关系。例如，数组可以转换为链表、栈或队列。

# 3. 单片机程序设计中常用数据结构

### 3.1 数组和链表

#### 3.1.1 数组的定义和操作

**定义：**

数组是一种线性数据结构，其中元素按顺序存储在连续的内存地址中。每个元素都有一个唯一索引，用于访问和操作。

**操作：**

* **访问元素：**通过索引访问特定元素，例如 `arr[i]`。
* **插入元素：**在指定索引处插入元素，需要移动后续元素。
* **删除元素：**删除指定索引处的元素，需要移动后续元素。
* **搜索元素：**通过线性搜索或二分搜索查找特定元素。
* **排序元素：**使用排序算法（如冒泡排序、快速排序）对元素进行排序。

#### 3.1.2 链表的定义和操作

**定义：**

链表是一种线性数据结构，其中元素存储在称为节点的动态分配内存中。每个节点包含数据和指向下一个节点的指针。

**操作：**

* **访问元素：**通过遍历链表，找到具有特定数据的节点。
* **插入元素：**在指定位置创建新节点并更新指针。
* **删除元素：**删除指定节点并更新指针。
* **搜索元素：**通过遍历链表查找特定数据。
* **排序元素：**使用排序算法（如归并排序、快速排序）对链表进行排序。

### 3.2 栈和队列

##