数据挖掘必修课：理论与实践结合的信息增益决策树构建指南

# 1. 数据挖掘与决策树概念解析

数据挖掘作为从大量数据中提取知识和见解的技术，在各个行业中发挥着日益重要的作用。在数据挖掘的众多算法中，决策树因其模型的直观性、易于理解以及强大的预测性能而备受青睐。在本章节中，我们将逐步解析决策树的基本概念，探讨其在数据挖掘过程中的应用，并为其后的深入学习打下坚实的基础。

## 1.1 数据挖掘的角色与重要性

数据挖掘涉及通过算法从大量数据中发现模式和关联，帮助企业和研究者在实际问题中做出更好的决策。随着大数据时代的到来，数据挖掘技术变得更为复杂和强大，为预测分析、用户行为分析、异常检测等领域提供了有力的支撑。

## 1.2 决策树算法简介

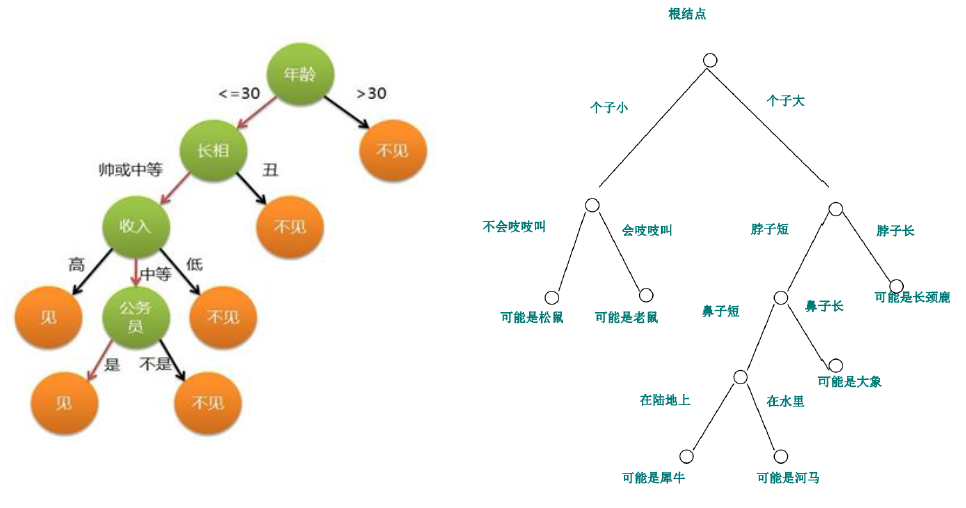
决策树是数据挖掘中的一种监督学习方法，它模拟人决策的思维过程，构建一种树形结构模型来表示决策的逻辑。每个内部节点代表对某个属性的判断，每个分支代表判断结果的输出，而每个叶节点则代表最终的决策结果或类别。

graph TD;
    A[开始] --> B[数据预处理]
    B --> C[特征选择]
    C --> D[构建决策树]
    D --> E[模型验证]
    E --> F[模型应用]

## 1.3 决策树的实际应用案例

决策树的实际应用非常广泛，比如在金融风控领域，通过分析客户信息和交易行为来评估贷款风险；在医疗诊断中，根据病人特征和症状预测疾病等。这些案例表明，决策树算法能够在多种情景下提供准确的预测结果。

在后续章节中，我们将深入探讨信息增益理论基础、决策树的构建和优化过程，以及如何在实际数据集上构建决策树模型。这一切都将为最终实现数据挖掘中的高级应用和决策树模型的评估与调优奠定基础。

# 2. 信息增益理论基础与计算方法

## 2.1 决策树的理论框架

### 2.1.1 决策树的定义与分类

决策树是一种被广泛用于分类和回归任务的机器学习算法。它以树形结构对数据进行分析，每棵树的内部节点代表一个属性上的测试，分支代表测试结果的分支，每个叶节点代表一种类别。决策树具有易于理解和解释的特点，它能够处理数值和非数值数据，也能处理缺失值。

决策树的分类可以根据不同的标准进行。按照学习方式划分，决策树主要分为监督学习的决策树和非监督学习的决策树。按照决策树的预测类型划分，分为分类决策树和回归决策树。分类决策树用于处理类别输出的问题，而回归决策树用于预测连续值。

### 2.1.2 决策树的构建过程概览

构建决策树的过程可以分为三个主要步骤：特征选择、决策树生成和决策树剪枝。

1. 特征选择：在每个节点上选择一个最优的特征，作为分裂标准。通常会计算信息增益、基尼不纯度或者增益比率等指标来衡量特征的重要性。
2. 决策树生成：基于选择的最优特征进行分裂，递归地创建子树，直至达到终止条件，例如树达到最大深度或者节点中的数据属于同一类别。
3. 决策树剪枝：通过剪枝减少决策树的复杂度，避免过拟合。剪枝可以是预剪枝（在生成树的过程中进行），也可以是后剪枝（在树生成之后进行）。

## 2.2 信息熵与信息增益

### 2.2.1 信息熵的概念和计算

信息熵是度量数据集纯度的一种方式，其概念来源于信息论。在决策树中，信息熵用来衡量一个节点纯度，节点的纯度越低，熵值越大；纯度越高，熵值越小。

信息熵的数学公式定义为：

H(S) = -∑p(x)log2(p(x))

其中，S是数据集，p(x)是数据集中属于类别x的概率。

信息熵的计算过程是对数据集中每个类别的出现概率进行加权求和，计算得到的熵值可以用来判断数据集的不确定性。

### 2.2.2 信息增益的计算和应用

信息增益是基于信息熵的概念，用来评估在给定数据集中，当使用某个特征进行分裂时能带来的信息熵减少量。通过计算信息增益，可以确定在每个节点应该选择哪个特征进行分裂。

信息增益的计算公式为：

Gain(S, A) = Entropy(S) - ∑[ (|Sv|/|S|) * Entropy(Sv) ]

其中，S表示数据集，A表示数据集中的某个特征，Entropy(S)表示分裂前的数据集熵，Entropy(Sv)表示分裂后各子集的熵值，|Sv|/|S|表示子集在整体数据集中的比例。

通过计算各个特征的信息增益，可以选出最佳分裂特征，这在决策树算法中至关重要。信息增益高的特征对于分类任务更有价值，因为它们能够减少输出结果的不确定性。

## 2.3 信息增益与决策树的优化

### 2.3.1 信息增益作为选择分裂属性的依据

在构建决策树的过程中，选择具有最高信息增益的属性进行分裂，能够有效地缩小数据集的不确定性，加快学习速度，并提高学习的准确率。信息增益是C4.5决策树算法的核心思想，也是在众多特征中选择分裂点的一种有效策略。

为了选择最优的分裂属性，可以构建一个信息增益表，其中列出所有特征的信息增益值。通过比较不同特征的信息增益值，选择信息增益最高的特征进行分裂，可以创建出一个更高效的决策树。

### 2.3.2 决策树的剪枝策略

尽管信息增益有助于提高决策树的分类能力，但过大的树模型可能会导致过拟合，即模型在训练数据上表现良好，但在未知数据上泛化能力差。因此，需要使用剪枝策略来简化决策树，提高模型的泛化能力。

剪枝策略可以分为预剪枝和后剪枝：

- 预剪枝：在生成决策树的过程中，通过提前停止树的生长来避免过拟合。例如，当数据集太小或者节点内数据的纯度已经足够高时，可以停止分裂该节点。
- 后剪枝：在完全生长的决策树基础上，移除一些分支以简化树结构。后剪枝通常比预剪枝更有效，因为它允许树先充分生长，然后再根据验证数据集来确定哪些分支是冗余的。

剪枝的目标是平衡模型复杂度和泛化能力。有效的剪枝策略可以显著提升模型性能，增强模型对新数据的预测能力。

【mermaid图示例】

graph TD
    A[开始构建决策树] --> B[选择最佳分裂特征]
    B --> C[信息增益最大的特征]
    C --> D[创建分支并分裂节点]
    D --> E{是否满足停止条件}
    E -- 是 --> F[完成当前节点分裂]
    E -- 否 --> B
    F --> G{是否满足剪枝条件}
    G -- 是 --> H[进行剪枝操作]
    G -- 否 --> I[继续生长树]
    H --> J[剪枝后决策树]
    I --> J

在上述mermaid流程图中，展示了决策树构建过程中的关键步骤。首先，算法通过选择最佳分裂特征来创建分支并分裂节点。然后，算法会检查是否满足停止条件，如果满足，则完成当前节点的分裂；如果不满足，它会回到选择最佳分裂特征的步骤。最终，算法会进行剪枝操作以避免过拟合，得到最终的决策树模型。

在实际应用中，选择最佳分裂特征和剪枝操作是通过计算信息增益和比较不同剪枝策略效果来进行的。通过上述步骤，可以构建出既能够准确分类数据，又能有效避免过拟合的决策树模型。

# 3. 基于信息增益的决策树构建实践

在深入探讨决策树构建的实践过程中，我们首先需要理解数据预处理的重要性，并掌握特征选择的方法。接着，我们将编写决策树算法代码，通过伪代码解释和关键代码段分析，展示如何将理论应用于实践。最后，我们将通过实际数据集的决策树构建来验证这些概念和技术。

## 数据预处理与特征选择

在数据挖掘的过程中，数据预处理是一个关键步骤，它直接影响到模型的性能。在构建决策树模型之前，我们必须确保数据的质量。

### 数据清洗与规范化

数据清洗涉及到识别和处理数据集中的缺失值、异常值和噪声。规范化则是将数据转换成统一的格式或缩放到一个特定范围，以便于算法处理。

import pandas as pd
from sklearn.preprocessing import MinMaxScaler

# 加载数据集
data = pd.read_csv('data.csv')

# 处理缺失值
data.fillna(data.mean(), inplace=True)

# 异常值处理（简单示例）
# 这里假设有一个名为'feature1'的列，我们将异常值替换为该列的均值
data['feature1'] = data['feature1'].apply(lambda x: x if (data['feature1'].min() <= x <= data['feature1'].max()) else data['feature1'].mean())

# 数据规范化
scaler = MinMaxScaler()
data[['feature1', 'feature2']] = scaler.fit_transform(data[['feature1', 'feature2']])

在上面的代码中，我们首先填充了数据集中的缺失值，然后对异常值进行了简