【Python二叉树与树结构实战】：构建与应用技巧揭秘

# 1. Python中树结构的基础概念

## 1.1 树的定义和术语
在计算机科学中，树是一种重要的非线性数据结构，它模拟了具有层级关系的数据。树由节点（Node）组成，其中每个节点可能有零个或多个子节点，这些子节点又可以有自己的子节点，形成分支。树结构广泛应用于编程语言的语法分析、数据库索引、文件系统等领域。

## 1.2 树的种类和特性
- **普通树**：每个节点可以有任意数量的子节点。
- **二叉树**：每个节点最多有两个子节点，通常称为左子节点和右子节点。
- **二叉搜索树（BST）**：二叉树的一种特殊形式，其中每个节点都满足左子树上所有元素小于该节点，右子树上所有元素大于该节点。
- **平衡树**：如AVL树，任何节点的两个子树的高度最大差别为1，确保树的操作效率。

## 1.3 树节点和层级
树由节点组成，每个节点包含数据和指向其子节点的链接。树的层级从根节点开始计算，根节点位于第一层，其子节点位于第二层，以此类推。树的深度是树中最大的层级数。在Python中，节点通常使用类来表示，包含数据、左链接和右链接等属性。

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

在后续章节中，我们将深入探讨如何构建、遍历、应用以及优化不同类型的树结构。现在，让我们从Python中树结构的基础概念开始，逐步深入到更复杂且实用的树操作。

# 2. 构建二叉树的算法与数据结构

## 2.1 二叉树的定义和性质

### 2.1.1 树节点的表示方法

在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”。在Python中实现一个二叉树节点可以使用以下方式：

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

这里，`value` 是存储在节点中的值，`left` 和 `right` 分别是左右子节点的引用。使用这种定义方法，我们可以方便地构建出各种复杂的二叉树结构。

### 2.1.2 二叉树的分类和特点

二叉树可以分为多种类型，每种类型都有其独特的结构和性质。比如：

- 完全二叉树：除了最后一层外，每一层都被完全填满，且所有节点都靠左排列。
- 满二叉树：每一层的节点数都达到最大值。
- 平衡二叉树：任一节点的两个子树的高度差不超过1。
- 二叉搜索树（BST）：对于任意节点，其左子树上所有节点的值小于该节点值，右子树上所有节点的值大于该节点值。

二叉树的这些分类和特点，为不同的应用场景提供了适应性强的数据结构。

## 2.2 二叉树的创建方法

### 2.2.1 手动创建和递归构建

创建二叉树通常有多种方法，手动创建简单直观，适合小型或静态的树结构。通过递归构建的方式则更加灵活，适合动态生成的树结构。例如，可以通过递归函数创建一个二叉树：

def create_binary_tree(elements, index=0):
    if index < len(elements) and elements[index] is not None:
        node = TreeNode(elements[index])
        node.left = create_binary_tree(elements, 2 * index + 1)
        node.right = create_binary_tree(elements, 2 * index + 2)
        return node
    return None

这个函数使用了一个列表 `elements` 来存储树的节点值，并根据索引位置决定左右子节点。

### 2.2.2 从数据序列生成二叉树

从数据序列生成二叉树是一种常见的创建方法，尤其是对于二叉搜索树。比如，我们可以将一个有序数组构造成一个平衡的二叉搜索树：

def sorted_array_to_bst(nums):
    if not nums:
        return None
    mid = len(nums) // 2
    node = TreeNode(nums[mid])
    node.left = sorted_array_to_bst(nums[:mid])
    node.right = sorted_array_to_bst(nums[mid+1:])
    return node

这个函数找到序列的中间元素作为根节点，并递归地构建左右子树。

## 2.3 二叉树的遍历算法

### 2.3.1 前序、中序和后序遍历

二叉树的遍历是树结构中非常重要的操作，常见的遍历方法有前序、中序和后序遍历。每种遍历方法代表了不同的节点访问顺序：

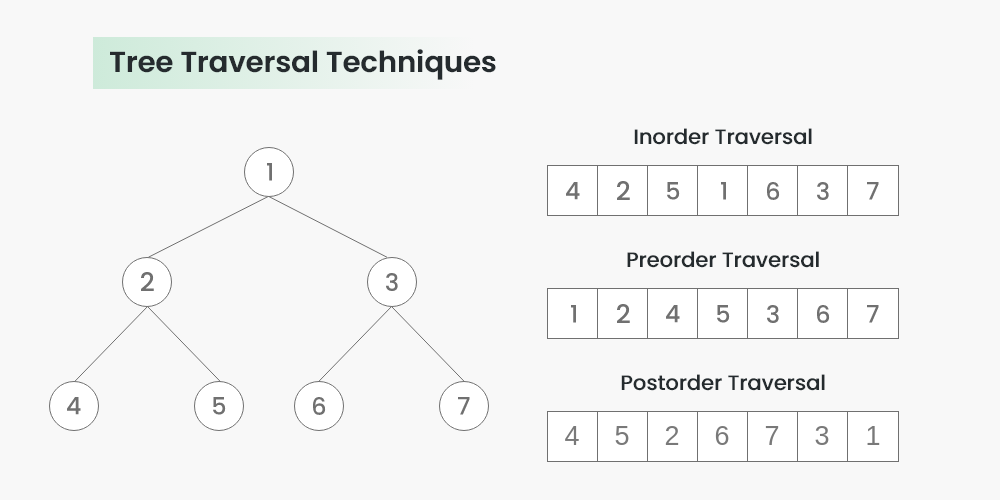
- 前序遍历：先访问根节点，然后遍历左子树，最后遍历右子树。
- 中序遍历：先遍历左子树，然后访问根节点，最后遍历右子树。
- 后序遍历：先遍历左子树，然后遍历右子树，最后访问根节点。

下面是一个二叉树遍历的示例：

def preorder_traversal(root):
    if root:
        print(root.value, end=' ')
        preorder_traversal(root.left)
        preorder_traversal(root.right)

### 2.3.2 层次遍历和广度优先搜索

层次遍历二叉树又称为广度优先搜索（BFS），它按照树的层次从上到下、从左到右的顺序访问每个节点。可以使用队列来实现：

from collections import deque

def level_order_traversal(root):
    if not root:
        return []
    queue = deque([root])
    result = []
    while queue:
        node = queue.popleft()
        result.append(node.value)
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)
    return result

### 2.3.3 深度优先搜索和递归遍历

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。在二叉树中，深度优先搜索通常通过递归实现。以下是一个深度优先搜索的中序遍历实现：

def inorder_traversal(root):
    result = []
    def dfs(node):
        if node:
            dfs(node.left)
            result.append(node.value)
            dfs(node.right)
    dfs(root)
    return result

递归方法直观地模拟了深度优先搜索的“深入”过程，在每个节点上进行操作，然后递归地进入子节点。

### 总结

在本章节中，我们详细介绍了二叉树的定义、分类、创建方法以及遍历算法。二叉树作为一种基础且广泛应用的数据结构，掌握其核心概念和操作对于理解更高级的数据结构和算法至关重要。通过手动构建二叉树和递归创建二叉树，我们了解了二叉树是如何从理论转化为实际编码操作的。而通过不同的遍历方法，我们学会了如何系统地访问和分析树中的每个节点。在后续章节中，我们将探索二叉树的更多高级应用和实践案例。

# 3. 二叉树的高级应用与实践

二叉树不仅仅是一种数据结构，其在实际应用中也展现出多方面的优势。本章节重点探讨二叉搜索树（BST）、平衡二叉树（AVL树）以及堆和优先队列这些二叉树的高级应用，并结合Python代码实践深入理解其内部机制与实现方式。

## 3.1 二叉搜索树（BST）的实现和应用

二叉搜索树（BST）是一种特殊的二叉树，它支持快速查找、插入和删除操作。它的每个节点都满足这样的性质：左子树上所有节点的值均小于它的根节点的值，右子树上所有节点的值均大于它的根节点的值。

### 3.1.1 BST的定义和性质

BST是一种有序树，这种有序特性使得BST在数据查找中尤其高效，其时间复杂度为O(log n)。然而，这种效率依赖于树的平衡性。在最理想的情况下，BST是一棵高度平衡的树，但在最坏的情况下，比如连续插入的有序序列，BST可能退化成一个链表，此时查找效率降为O(n)。

### 3.1.2 插入、查找和删除操作

在Python中实现BST的插入操作，需要递归地比较节点值，并相应地插入到左子树或右子树中。查找操作则通过比较目标值与节点值，决定是向左子树还是右子树递归查找，或者直接找到目标值。删除操作相对复杂，因为需要处理删除节点后子树的重新连接问题，具体情况分为三种：

- 被删除的节点没有子节点
- 被删除的节点有一个子节点
- 被删除的节点有两个子节点

以下是使用Python实现BST及其基本操作的代码示例：

class TreeNode:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None

class BST:
    def __init__(self):
        self.root = None

    def insert(self, key):
        self.root = self._insert(self.root, key)

    def _insert(self, node, key):
        if node is None:
            return TreeNode(key)
        if key < node.key:
            node.left = self._insert(node.left, key)
        elif key > node.key:
            node.right = self._insert(node.right, key)
        return node

    def search(self, key):
        return self._search(self.root, key)

    def _search(self, node, key):
        if node is None or node.key == key: