【MATLAB对比分析】:圆柱螺线与圆锥螺线的三维图形绘制技巧
发布时间: 2025-01-09 12:29:52 阅读量: 11 订阅数: 11 


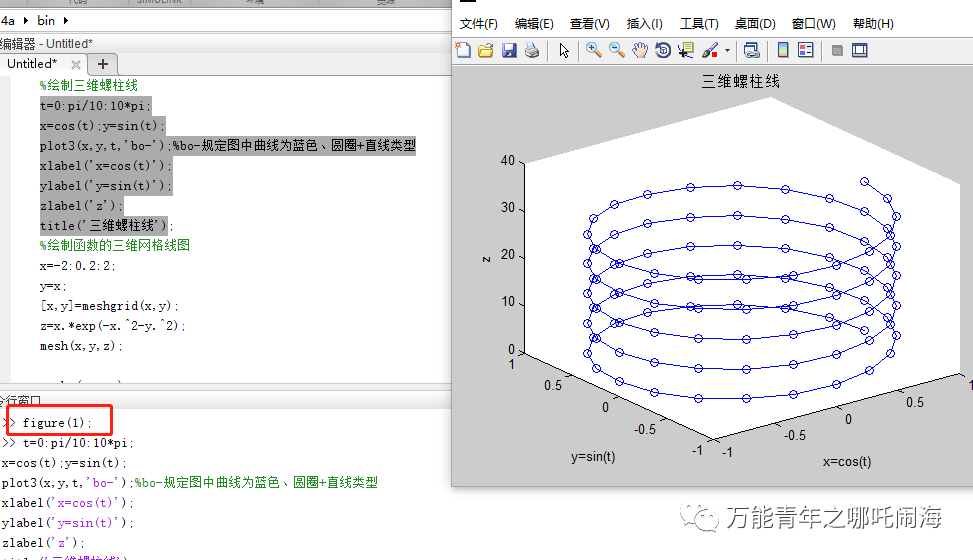
MATLAB绘制考纽螺线(回旋螺线)
# 摘要
本文首先回顾了MATLAB的基础知识,为后续图形绘制打下基础。接着详细探讨了圆柱螺线与圆锥螺线的数学理论,并介绍了它们在MATLAB中的基本及高级三维图形绘制技巧。文章通过对绘制方法、颜色与线型定制、光照和材质效果的分析,展示了如何使用MATLAB更生动和专业地表现这些螺线。此外,通过对比分析圆柱螺线与圆锥螺线的形态特征、编程实现及应用场景,本文提供了一个全面的理解和运用这些数学概念和计算机绘图技术的视角。本文旨在为工程技术人员提供圆柱螺线和圆锥螺线在MATLAB环境下图形绘制与分析的实践指南。
# 关键字
MATLAB;圆柱螺线;圆锥螺线;三维图形绘制;颜色线型定制;光照材质效果
参考资源链接:[圆柱螺线和圆锥螺线-MATLAB绘图](https://wenku.csdn.net/doc/6fy0emkbpj?spm=1055.2635.3001.10343)
# 1. MATLAB基础知识回顾
## 1.1 MATLAB简介
MATLAB是一种高性能的数值计算环境和第四代编程语言,广泛应用于工程计算、数据分析、算法开发等领域。其强大的数学函数库和可视化工具箱使得MATLAB成为工程师和科研人员不可或缺的工具之一。
## 1.2 MATLAB基本操作
在MATLAB中,基本操作包括矩阵运算、数据可视化、函数绘图等。用户可以通过命令窗口输入指令或编写脚本进行自动化操作。
### 1.2.1 矩阵和数组操作
MATLAB的核心是矩阵运算,因此掌握矩阵的创建、修改和操作是使用MATLAB的基础。例如,创建矩阵:
```matlab
A = [1 2 3; 4 5 6; 7 8 9]
```
### 1.2.2 数据可视化
MATLAB提供了多种函数用于绘制二维和三维图形。例如,绘制二维散点图:
```matlab
x = [1 2 3 4 5];
y = [2 3 1 5 4];
scatter(x, y)
```
### 1.2.3 函数绘图
函数绘图是展示数学函数图像的便捷方式。例如,绘制正弦函数图像:
```matlab
fplot('sin(x)', [0, 2*pi])
```
通过上述内容,我们可以对MATLAB有一个初步的认识,接下来将深入探讨圆柱螺线与圆锥螺线的数学理论,并结合MATLAB的绘图技巧进行详细介绍。
# 2. 圆柱螺线与圆锥螺线的数学理论
### 2.1 圆柱螺线的基本概念和属性
圆柱螺线是一类在数学和工程领域中常见的三维螺旋形状,它们的数学描述基于圆柱坐标系。在实际应用中,圆柱螺线可以体现为自然界中的各种螺旋结构,比如贝壳、DNA分子的螺旋结构等。在数学上,圆柱螺线的参数方程可以表示为:
```
x = r * cos(θ)
y = r * sin(θ)
z = k * θ
```
其中,`r` 是半径,`θ` 是角度(通常从0到2π或者更多,取决于螺线的完整程度),而`k`是螺旋线的螺距常数,决定了螺线的紧密程度。随着`θ`的增加,点沿着z轴的正方向螺旋上升。
### 2.2 圆锥螺线的基本概念和属性
圆锥螺线,又称为对数螺线,是一类在自然界中广泛出现的螺旋形结构,其特点是螺线的形状在放大或缩小后仍保持不变。圆锥螺线的参数方程在笛卡尔坐标系中可以表达为:
```
x = a * e^(b * θ) * cos(θ)
y = a * e^(b * θ) * sin(θ)
```
在上式中,`a` 和 `b` 是常数,它们决定了螺线的形状和大小。`θ` 是角度变量,从0增加到无穷大时,螺线会形成一个无界的螺旋。
### 2.3 圆柱螺线与圆锥螺线的数学对比
圆柱螺线和圆锥螺线在数学描述上有明显的不同。圆柱螺线在z轴方向是线性的,而圆锥螺线在径向随着角度的增加呈指数级增长。因此,圆锥螺线在视觉上会显得更加“密集”,而且它的螺旋形状是等比例放大的。
在数学分析中,这两类螺线的几何性质也有所区别。圆柱螺线具有恒定的螺距,而圆锥螺线的螺距随着半径的增加而增加。当分析这两种螺线的特性时,研究者可能会利用微积分、线性代数等数学工具来进行深入研究。
### 2.4 数学模型的物理意义
数学模型不仅仅是抽象的符号表达,它们往往有着实际的物理意义。例如,圆柱螺线在物理学中可以描述某些粒子在磁场中的螺旋运动轨迹,而圆锥螺线则能描绘出生物体的生长模式。在工程学上,这些螺线模型可以用于设计弹簧、天线等结构。
### 2.5 数学理论在现实世界的应用
数学理论在解释和预测现实世界中的现象方面发挥着关键作用。圆柱螺线和圆锥螺线作为数学模型,同样在各个领域有着广泛的应用。
例如,当研究DNA结构时,DNA分子的双螺旋可以近似看作是圆柱螺线的一种形态。而在天文学中,螺旋星系的形状近似为圆锥螺线。此外,在计算机图形学中,这些螺线模型可用于生成复杂且自然的螺旋图案。
### 2.6 数学理论的深入研究方向
尽管圆柱螺线与圆锥螺线的数学理论已经相当成熟,但科学家和数学家依然在探索这些模型的新用途和进一步的性质。例如,研究者们可能对如何将这些螺线模型应用于新型材料的设计、如何在数据可视化中使用螺线来展示信息,或者是在量子物理学中,如何用它们来描述粒子的行为。
在未来的科技发展过程中,这些数学模型的理论可能还会用于开发出更加高级的技术,如改进的导航系统、高密度数据存储解决方案,甚至是新型的能源产生和储存系统。
# 3. MATLAB中的三维图形绘制基础
MATLAB不仅仅是一个高级数学计算工具,它在三维图形的绘制上也具有强大的功能。掌握MATLAB中的三维图形绘制对于工程师和科研工作者来说是必不可少的技能。在这一章节中,我们将从基础出发,逐步深入探讨如何使用MATLAB绘制出令人印象深刻的三维图形。
## 3.1 基本的三维图形函数
在MATLAB中,绘制三维图形主要依赖于一些基本的函数,如`plot3`、`mesh`和`surf`等。我们首先来介绍这些基础函数的使用方法。
### 3.1.1 plot3函数
`plot3`函数是绘制三维线图的基础,它能够根据给定的三个坐标向量绘制出空间中的点,并且将这些点按顺序连接起来。
```matlab
% 绘制一个简单的三维空间线图
x = [1:10];
y = [5:5:50];
z = [10:-1:1];
plot3(x, y, z);
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
title('3D Line Plot Using plot3');
```
上面的代码将生成一个三维空间中的线性图形,其中`xlabel`、`ylabel`、`zlabel`和`title`函数分别用于设置坐标轴标签和图形标题。
### 3.1.2 mesh函数
`mesh`函数用于生成三维网格图,它会显示每个数据点的网格连接,但不会填充网格之间的区域。
```matlab
[X, Y] = meshgrid(1:0.5:10, 1:0.5:10);
Z = sin(sqrt(X.^2 + Y.^2));
mesh(X, Y, Z);
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
title('3D Mesh Plot');
```
在上述例子中,`meshgrid`函数用于生成X和Y的数据网格,然后通过`sin`函数计算出Z的值,并用`mesh`函数绘制出来。
### 3.1.3 surf函数
与`mesh`类似,`surf`函数用于绘制三维表面图。但不同的是,`surf`会在网格之间的区域填充颜色,提供了更丰富的视觉效果。
```matlab
[X, Y] = meshgrid(-5:0.25:5, -5:0.25:5);
Z = peaks(X, Y);
surf(X, Y, Z);
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
title('3D Surface Plot');
```
在这个例子中,`peaks`是一个MATLAB内置函数,用于生成测试用的三维曲面数据。`surf`函数绘制了这个曲面并填充了颜色。
## 3.2 三维图形的视觉效果增强
在绘制基本的三维图形之后,我们往往会希望增加图形的视觉效果,使得图形更加生动和易于理解。
### 3.2.1 视角调整
MATLAB提供了几个视角调整函数,比如`view`、`rotate3d`、`camdolly`、`camorbit`和`campan`等,可以用来从不同角度观察三维图形。
```matlab
figure;
surf(X, Y, Z);
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
title('3D Surface Plot with View Control');
view(30, 30); % 调整视角为30度仰角和30度方位角
```
上面的代码中,`view(30, 30)`设置了图形的观察角度为30度仰角和30度方位角,使图形展示更加立体。
### 3.2.2 光照和颜色
在三维图形中添加光照效果和自定义颜色可以使图形更加生动。MATLAB提供了`camlight`和`lighting`函数来添加和控制光照。
```matlab
figure;
surf(X, Y, Z);
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
title('3D Surface Plot with Lighting Effects');
camlight right; % 在右侧添加光源
lighting gouraud; % 设置光照效果为Gouraud着色
```
在此代码中,`camlight right`命令在图形的右侧添加了一个光源,而`lighting gouraud`则是设置光照效果为Gouraud着色,这样可以使曲面看起来更平滑,更具立体感。
## 3.3 实例:绘制三维螺旋线
为了更好地理解MATLAB在三维图形绘制方面的应用,我们将通过一个实例——绘制三维螺旋线——来综合运用本章节所学的知识。
### 3.3.1 螺旋线的数学模型
三维螺旋线可以使用参数方程来表示。这里,我们将以圆柱螺旋线为例,其参数方程为:
```matlab
% 圆柱螺旋线参数方程
t = linspace(0, 10*pi, 1000); % 生成参数向量
x = 10 * cos(t); % X轴坐标
y = 10 * sin(t); % Y轴坐标
z = t; % Z轴坐标
% 绘制螺旋线
plot3(x, y, z);
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
title('3D Helix Plot');
```
这段代码定义了一个圆柱螺旋线,并使用`plot3`函数绘制出来。螺旋线随着参数`t`的增加而一圈圈上升。
### 3.3.2 美化螺旋线
为了让螺旋线更加美观,我们可以添加颜色和光照效果:
```matlab
figure;
h = plot3(x, y, z, 'r-'); % 使用红色线条绘制
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
title('3D Helix Plot with Color and Lighting');
% 添加光照效果
camlight left; % 在左侧添加光源
lighting phong; % 设置光照效果为Phong着色
set(h, 'LineWidth', 2); % 设置线宽为2
```
在这段代码中,我们使用了`camlight`函数在螺旋线的左侧添加了一个光源,并通过`lighting phong`命令应用了Phong着色。我们还通过`set`函数改变了螺旋线的颜色和线宽,使其看起来更醒目。
通过上述章节内容的介绍,我们已经搭建了MATLAB三维图形绘制的基础框架,了解了如何绘制基本图形、如何增强视觉效果以及如何通过实际案例来综合运用这些知识。接下来的章节中,我们将更详细地探讨圆柱螺线和圆锥螺线的绘制技巧,并将这些技巧应用到具体实例中,使我们的图形绘制能力进一步提升。
# 4. 圆柱螺线的MATLAB绘制技巧
## 4.1 基本绘制方法
圆柱螺线是一种在三维空间中按照特定规则螺旋上升的曲线。了解其数学表达式是绘制这种螺线的第一步。圆柱螺线可以用参数方程来定义,这个方程描述了螺线在三维空间中的坐标。
### 4.1.1 参数方程的定义
圆柱螺线的参数方程一般形式如下:
```matlab
x = r * cos(t)
y = r * sin(t)
z = a * t
```
这里,`r` 是螺线的径向常数,`a` 是螺线的轴向常数,`t` 是参数,从0到无穷大变化。
### 4.1.2 使用plot3函数进行绘制
在MATLAB中,我们可以使用 `plot3` 函数绘制基于上述参数方程的圆柱螺线。下面是一个简单的例子:
```matlab
t = linspace(0, 10*pi, 1000); % 从0到10π的参数t
r = 1; % 径向常数设置为1
a = 1; % 轴向常数也设置为1
x = r * cos(t);
y = r * sin(t);
z = a * t;
plot3(x, y, z);
grid on;
xlabel('X');
ylabel('Y');
zlabel('Z');
title('圆柱螺线基本绘制');
```
这段代码将生成一条从原点开始,沿着Z轴无限延伸的圆柱螺线。
## 4.2 高级绘制技巧
在基本绘制方法上,我们可以进一步定制圆柱螺线的视觉效果,包括其颜色、线型、光照和材质等。
### 4.2.1 螺线的颜色和线型定制
我们可以通过修改 `plot3` 函数的调用来改变线型和颜色。例如,以下代码展示了如何使用红色虚线来绘制圆柱螺线:
```matlab
plot3(x, y, z, 'r--');
```
此外,我们可以使用 `line` 函数来更细致地控制线条属性:
```matlab
h = line(x, y, z);
set(h, 'LineStyle', '--', 'Color', 'r');
```
### 4.2.2 螺线的光照和材质效果
MATLAB提供了多种方式来添加光照和材质效果,使得三维图形更加生动和逼真。例如,可以使用 `light` 和 `lighting` 函数来添加光源和调整光照效果:
```matlab
light('Position', [5, 5, 5]); % 添加一个位于[5, 5, 5]的光源
lighting phong; % 使用Phong光照模型
material dull; % 设置材质为无光泽
```
## 4.3 实践案例分析
为了加深理解,我们通过两个实例来展示如何动态展示和交互式绘制圆柱螺线。
### 4.3.1 实例1:动态展示圆柱螺线
动态展示圆柱螺线可以让我们更好地理解其三维结构。我们可以使用 `for` 循环结合 `drawnow` 函数来实现:
```matlab
figure;
for i = 1:0.1:10
z = a * i;
plot3(x, y, z);
drawnow;
pause(0.1);
end
```
这段代码会逐渐增加圆柱螺线的长度,并实时更新图形窗口。
### 4.3.2 实例2:交互式圆柱螺线绘制
在MATLAB中,我们可以创建一个交互式的圆柱螺线绘制环境。通过编写一个GUI程序,用户可以输入不同的参数值来观察螺线的变化。这需要用到 `uicontrol` 函数和回调函数:
```matlab
hFig = figure('Position', [100, 100, 500, 300]);
hEditR = uicontrol('Style', 'edit', 'String', '1', 'Position', [50, 250, 50, 25]);
hEditA = uicontrol('Style', 'edit', 'String', '1', 'Position', [150, 250, 50, 25]);
hButtonPlot = uicontrol('Style', 'pushbutton', 'String', '绘制', 'Position', [250, 250, 50, 25], 'Callback', @PlotHelix);
function PlotHelix(~, ~)
r = str2num(get(hEditR, 'String'));
a = str2num(get(hEditA, 'String'));
t = linspace(0, 10*pi, 1000);
x = r * cos(t);
y = r * sin(t);
z = a * t;
plot3(x, y, z);
end
```
这段代码创建了一个简单的界面,用户可以输入不同的 `r` 和 `a` 值,点击“绘制”按钮后,就会绘制出相应的圆柱螺线。
# 5. 圆锥螺线的MATLAB绘制技巧
## 5.1 基本绘制方法
### 5.1.1 参数方程的定义
圆锥螺线(Conical Helix)是一种在三维空间中沿圆锥面螺旋上升的曲线。其参数方程通常表示为:
```math
x = (r \cdot cos(\theta))
y = (r \cdot sin(\theta))
z = b \cdot \theta / (2\pi)
```
其中 `r` 是基圆半径,`θ` 是角度变量,`b` 是螺线沿锥轴的螺旋率。
在MATLAB中,这些参数可以通过向量或变量来定义。
### 5.1.2 使用plot3函数进行绘制
在MATLAB中,我们可以使用`plot3`函数绘制基本的圆锥螺线。例如,给定 `r = 1` 和 `b = 1` 的参数方程,绘制圆锥螺线的代码如下:
```matlab
% 定义参数
r = 1; % 基圆半径
b = 1; % 螺旋率
theta = linspace(0, 2*pi*5, 500); % 角度变量,范围从0到10圈
% 计算x, y, z坐标
x = r * cos(theta);
y = r * sin(theta);
z = b * theta / (2 * pi);
% 绘制圆锥螺线
plot3(x, y, z);
grid on;
xlabel('X axis');
ylabel('Y axis');
zlabel('Z axis');
title('Conical Helix');
```
此代码段首先定义了圆锥螺线的参数,然后计算了对应的坐标,并使用`plot3`函数将其绘制出来。
## 5.2 高级绘制技巧
### 5.2.1 螺线的颜色和线型定制
在MATLAB中,我们可以通过`plot3`函数的属性来定制螺线的颜色和线型。下面是一个例子,展示了如何改变线条颜色为红色,并使用点线样式:
```matlab
h = plot3(x, y, z, 'r--');
```
这里,`'r--'`指定了红色的点线样式,`h`是返回的线条句柄,可以用来进一步修改线条属性。
### 5.2.2 螺线的光照和材质效果
为了增强图形的视觉效果,我们可以添加光照和材质效果。以下是添加光照和材质的MATLAB代码示例:
```matlab
% 设置材质为金属
material shiny;
% 添加光源
camlight left; % 在摄像机左侧添加一个光源
lighting gouraud; % 设置光照模式为Gouraud
% 更新绘图
drawnow;
```
此代码段首先设置了材质属性,然后在摄像机的左侧添加了一个光源,并且指定了光照模式为Gouraud,这种模式可以提供平滑的着色效果。
## 5.3 实践案例分析
### 5.3.1 实例1:动态展示圆锥螺线
动态展示可以通过改变角度范围或螺旋圈数来实现。以下是一个动态绘制圆锥螺线的示例:
```matlab
% 定义参数
r = 1;
b = 1;
n = 10; % 总圈数
% 生成角度范围
theta = linspace(0, 2*pi*n, 500*n);
% 循环绘制每一圈
for k = 1:n
% 计算当前圈的x, y, z坐标
x = r * cos(theta((k-1)*500+1:k*500));
y = r * sin(theta((k-1)*500+1:k*500));
z = b * theta((k-1)*500+1:k*500) / (2 * pi);
% 绘制当前圈
plot3(x, y, z, 'b');
axis equal; % 等轴比例
pause(0.1); % 暂停一小段时间以便观察动态效果
drawnow;
end
```
这段代码通过循环每圈绘制并使用`pause`函数来实现动态效果。
### 5.3.2 实例2:交互式圆锥螺线绘制
我们可以使用MATLAB的交互式功能来创建一个用户界面,让用户输入不同的参数来绘制圆锥螺线。以下是一个简单的交互式绘图界面的代码示例:
```matlab
function interactive_conical_helix()
% 创建图形窗口
hFig = figure('Name', 'Interactive Conical Helix');
% 创建用户界面元素
uicontrol('Style', 'text', 'Position', [10 100 100 30], 'String', 'Enter parameters:');
rEdit = uicontrol('Style', 'edit', 'Position', [120 100 50 30], 'String', '1');
bEdit = uicontrol('Style', 'edit', 'Position', [180 100 50 30], 'String', '1');
btnPlot = uicontrol('Style', 'pushbutton', 'Position', [240 100 100 30], 'String', 'Plot', 'Callback', @plotHelix);
% 绘图函数
function plotHelix(~, ~)
r = str2double(get(rEdit, 'String'));
b = str2double(get(bEdit, 'String'));
theta = linspace(0, 2*pi*5, 500);
x = r * cos(theta);
y = r * sin(theta);
z = b * theta / (2 * pi);
plot3(x, y, z);
end
end
% 调用函数启动交互界面
interactive_conical_helix();
```
这段代码创建了一个交互式用户界面,允许用户输入半径和螺旋率来绘制圆锥螺线。用户点击"Plot"按钮后,会调用绘图函数`plotHelix`。
通过以上章节内容,我们可以看到圆锥螺线的绘制不仅要求我们理解其背后的数学原理,还需要通过编程技巧在MATLAB中实现其图形的绘制。在这一过程中,基本绘制方法、颜色和线型定制、光照和材质效果的高级技巧,以及交互式与动态展示的实现,都显得至关重要。这些方法和技巧的熟练运用,将使得在MATLAB中进行图形绘制变得更加灵活和富有表现力。
0
0






