MATLAB动态展示：圆锥螺线的视觉优化与交互式绘图


# 摘要
本文系统探讨了圆锥螺线的数学基础、MATLAB绘图技术及其动态展示和交互式应用。首先介绍了圆锥螺线的数学原理和MATLAB绘图基础，包括基本绘图命令、动态效果实现、图形视觉优化策略。随后，文章通过参数方程的MATLAB实现，探讨了动态展示的编程技巧以及视觉优化案例分析。接着深入交互式绘图技术，讨论了界面设计、数据驱动动态图形以及高级交互式功能的开发。最后，结合圆锥螺线在科学可视化和教育领域的应用，展望了交互式可视化未来的发展趋势与技术挑战。本文旨在为从事相关领域的研究者和开发者提供全面的技术参考和实践指导。

# 关键字
圆锥螺线；MATLAB绘图；动态展示；交互式界面；数据可视化；科学模型

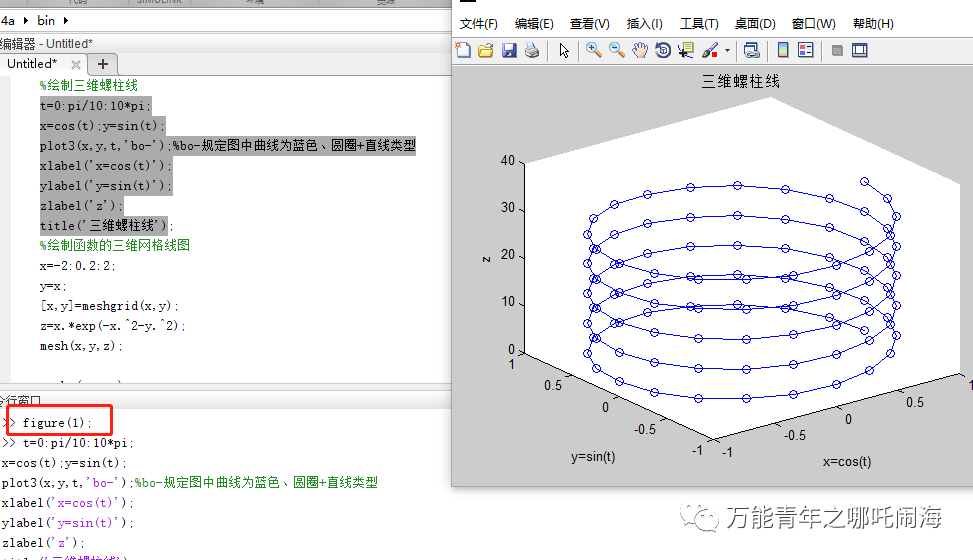
参考资源链接：[圆柱螺线和圆锥螺线-MATLAB绘图](https://wenku.csdn.net/doc/6fy0emkbpj?spm=1055.2635.3001.10343)
# 1. 圆锥螺线的数学基础

圆锥螺线是一种常见的数学曲线，在自然科学和工程技术领域有着广泛的应用。本章我们将简要介绍圆锥螺线的基本数学概念，包括其定义、数学方程以及相关属性，为后续在MATLAB环境下进行可视化展示打下坚实的理论基础。

## 1.1 圆锥螺线的定义与性质
圆锥螺线（Conical Helix）是空间中的一种螺旋线，它的特点是螺线上的每一点到某固定直线的距离与其沿该直线的投影的距离成正比。圆锥螺线可以被看作圆周运动和直线运动的合成，其轨迹在三维空间中形成一个螺旋上升或下降的形状。

## 1.2 数学方程与参数表达
圆锥螺线可以通过参数方程来描述，常见的参数化形式如下：
\[ x(t) = r \cdot \cos(t), \]
\[ y(t) = r \cdot \sin(t), \]
\[ z(t) = b \cdot t, \]
其中，\( r \) 和 \( b \) 是常数，分别代表螺线半径和螺距。参数 \( t \) 表示旋转角度。此方程组定义了圆锥螺线在三维空间中的位置，其中 \( r \) 控制着螺线的圆周半径，\( b \) 控制螺距的大小，决定了螺线的疏密程度。

## 1.3 几何特性与应用
圆锥螺线的几何特性使其在众多领域中有着广泛应用，比如在机械工程中用于设计螺纹，而在计算机图形学中则用于生成复杂的螺旋效果。理解其基本数学特性，有助于在各种应用中进行有效利用。

通过以上内容，我们已经对圆锥螺线有了初步的了解，接下来我们将进入第二章，学习如何使用MATLAB软件将这些数学概念转化为可视化图形。

# 2. MATLAB绘图基础与优化方法

## 2.1 MATLAB的基本绘图命令

### 2.1.1 简单图形的创建与绘制

在MATLAB中创建和绘制简单图形是学习更复杂绘图技术的基础。MATLAB 提供了多种函数来绘制常见的二维和三维图形。例如，`plot` 函数用于生成二维图形，`meshgrid` 和 `surf` 函数用于创建和绘制三维曲面图形。

在MATLAB中，绘制一个基本的二维线图非常简单：

x = 0:0.01:10;
y = sin(x);
plot(x, y);
xlabel('x-axis');
ylabel('sin(x)');
title('Sine Wave');

在上述代码中，`x` 是一个从0到10的向量，步长为0.01。`y` 是 `x` 的正弦函数值。`plot` 函数将 `x` 和 `y` 的值绘制为线图，并使用 `xlabel`、`ylabel` 和 `title` 函数添加坐标轴标签和标题。

二维图形的绘制还包括散点图、柱状图、饼图等。而三维图形的绘制，如三维线图、曲面图、等高线图等，则是通过 `plot3`、`mesh`、`surf` 等函数实现。通过这些基础函数，可以构建出更加复杂的视觉效果。

### 2.1.2 图形属性的设置与优化

MATLAB允许用户对图形的属性进行详细设置，包括颜色、线型、标记点类型等。通过这些设置可以增强图形的可读性和美观性。例如，我们可以改变线条颜色、宽度和样式：

plot(x, y, 'r--', 'LineWidth', 2);

在这个命令中，`'r--'` 表示红色的虚线，`'LineWidth', 2` 设置了线条的宽度为2个单位。

在绘图时，还可以添加图例、网格线、坐标轴标签等来提供更多信息，提高图形的专业性。以下是一个具有多个属性设置的示例：

plot(x, y, 'g', 'LineWidth', 2);
grid on; % 添加网格线
legend('Sine function'); % 添加图例
xlabel('Time (s)');
ylabel('Amplitude');
title('Sine Wave with Attributes');

通过对图形属性的调整和优化，可以使得图形更加清晰、易于理解和展示。此外，对于图形的优化还包括性能优化，比如减少绘图指令的复杂度和优化绘图命令以减少内存使用。

## 2.2 动态效果的实现技术

### 2.2.1 动画的生成原理

在MATLAB中，动态效果通常是通过逐帧绘制和更新图形来实现的。动画的生成原理涉及到快速连续显示多张静态图像，每张图像间呈现细微差异，从而在视觉上形成动态效果。在MATLAB中，可以利用循环结构来生成动画。

for t = 0:0.01:10
    x = 0:t;
    y = sin(x);
    plot(x, y);
    drawnow; % 立即更新图形窗口
    pause(0.01); % 暂停10毫秒，以减慢动画速度
end

在上述代码中，通过 `for` 循环逐步增加 `x` 的值并更新 `y` 的值，再用 `plot` 函数绘制。`drawnow` 函数确保每一帧的图形都能即时更新在图形窗口中，而 `pause` 函数则用于控制动画的播放速度。

### 2.2.2 时间控制与帧率优化

帧率是动画流畅度的关键，它是指动画中每秒钟播放的帧数（fps）。MATLAB在处理数据密集型任务时可能会受限于其性能，因此帧率控制是实现高质量动画的另一个重要方面。帧率过高或过低都可能影响动画的观看体验。

fps = 30; % 设置目标帧率为30 fps
maxwait = 1/fps; % 计算每个循环的最大等待时间
for t = 0:0.01:10
    % 绘图代码
    ...
    drawnow;
    remaining = maxwait - etime tic, toc; % 计算剩余时间并等待
    if remaining > 0
        pause(remaining);
    end
end

上述代码通过设置目标帧率并使用 `tic` 和 `toc` 函数来监控时间，调整 `pause` 函数的参数，以确保动画的帧率尽可能接近设定的目标帧率。这样可以实现更加平滑和连贯的动画效果，并且有效控制了图形绘制的性能消耗。

通过适当调整动画生成过程中的时间控制，开发者可以优化图形的性能，以适应不同的应用场景。例如，在实时数据可视化时，可能需要较高的帧率来展示动态变化；而在播放预渲染动画时，则可以接受较低的帧率以节省计算资源。

## 2.3 图形视觉优化策略

### 2.3.1 色彩和光影的搭配技巧

色彩和光影对于图形的视觉表现至关重要。合适的色彩搭配可以突出图形中的关键信息，而光影的运用则能够增强图形的立体感和空间感。

在MATLAB中，可以通过设置颜色和调整光照和材质属性来优化图形的视觉效果。例如，使用 `colormap` 函数可以更改图形的色彩映射表，以便更好地展示数据变化。

colormap(jet); % 将色彩映射表设置为“jet”色彩映射

为了在图形中添加光照效果，可以使用 `camlight` 和 `lighting` 函数。`camlight` 函数会在相机位置添加一个光源，而 `lighting` 函数则用来控制图形的光照模式。例如：

camlight left; % 在相机左侧添加光源
lighting phong; % 使用Phong光照模型增强图形的立体感

### 2.3.2 空间布局与视角变换

空间布局和视角变换是优化图形视觉的另一个重要方面。通过调整图形在三维空间中的位置和观察角度，可以更有效地展示图形的细节和结构。

在MATLAB中，可以通过改变坐标轴属性来调整视角，使用 `view` 函数可以指定观察图形的角度：

view(3); % 设置为三维视图
axis equal; % 设置坐标轴比例相等

此外，`rotate` 函数可以用来旋转图