递归函数的高级应用

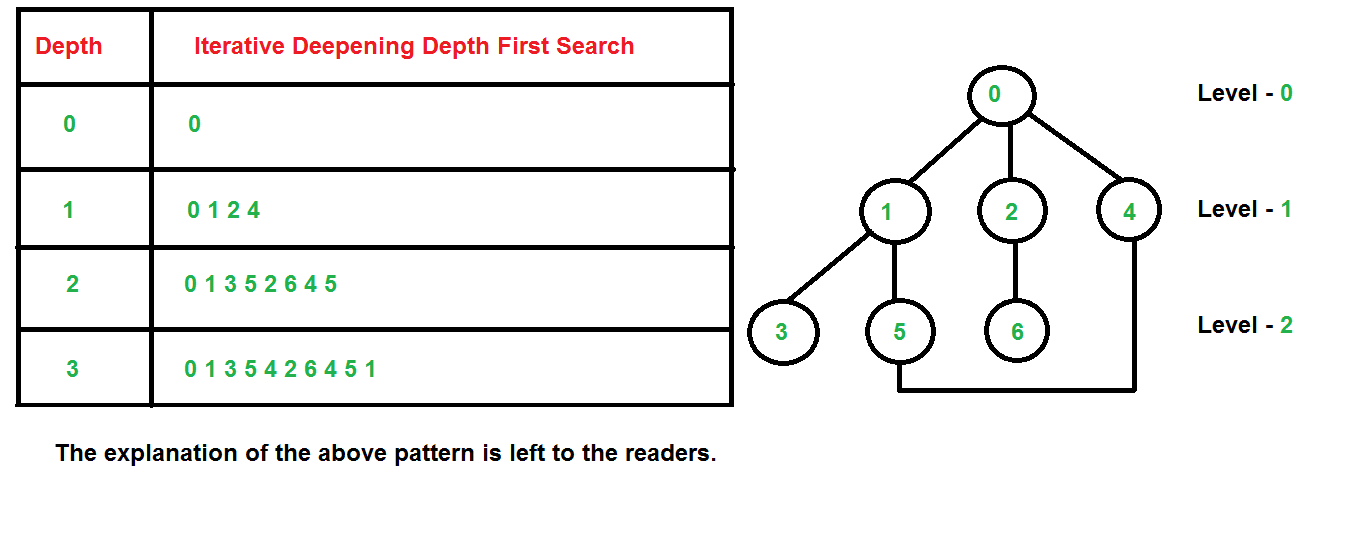
# 1. 递归函数的理论基础

## 1.1 递归的定义和核心要素

递归是一种程序设计的技巧，它允许一个函数调用自身来解决问题。核心要素包括递归基准条件（基本情况）和递归步骤。在基准条件中，问题被简化到可以直接得出答案的程度。递归步骤则是将问题分解为更小的子问题，并调用自身函数来解决这些子问题。

### 代码块示例（Python）

def factorial(n):
    # 基准条件
    if n == 0:
        return 1
    # 递归步骤
    else:
        return n * factorial(n-1)

在这个阶乘函数中，当`n`为0时，函数直接返回1（基准条件），否则函数返回`n`乘以`n-1`的阶乘值（递归步骤）。

## 1.2 递归的原理和应用环境

递归的原理基于数学归纳法，它利用了函数自身的调用来重复执行任务，直到达到某种终止条件。在数据结构和算法中，递归可用于树的遍历、图的搜索、排序算法等。递归提供了一种自然、直观的问题解决方法，但在计算上可能比迭代方法消耗更多的资源，特别是在处理大型数据集时。

## 1.3 递归的优缺点分析

递归的优点是能够以更简洁、更直观的代码解决问题，特别是在解决可以自然分解为更小子问题的任务时。它的缺点包括可能造成栈溢出和较高的运行时开销。理解递归的优缺点对于掌握何时使用递归以及如何优化递归代码至关重要。

接下来，我们将探讨递归函数在数据结构中的应用。

# 2. 递归函数在数据结构中的应用

## 2.1 树形结构的遍历与操作

### 2.1.1 前序、中序和后序遍历

树形结构作为数据结构中的一个重要组成部分，在计算机科学领域中有着广泛的应用。树的遍历是指按照一定的规则访问树中的每个节点，而不重复地进行一次操作。根据节点被访问的先后顺序不同，树的遍历可以分为前序遍历、中序遍历和后序遍历。

前序遍历是一种深度优先遍历方法，它按照“根-左-右”的顺序访问树的每个节点。即首先访问树的根节点，然后递归地进行前序遍历左子树，接着递归地进行前序遍历右子树。前序遍历的时间复杂度为O(n)，其中n是树中节点的数量。

中序遍历是指先访问左子树，然后访问根节点，最后访问右子树，即“左-根-右”。中序遍历的一个重要应用是二叉搜索树的有序遍历，它能够按照从小到大的顺序访问树中所有的节点。中序遍历的时间复杂度同样为O(n)。

后序遍历则是先访问左子树，然后访问右子树，最后访问根节点，即“左-右-根”。后序遍历在计算树的深度和高度以及删除树结构时非常有用。时间复杂度同为O(n)。

下面的伪代码展示了前序遍历的基本实现：

procedure preorderTraversal(node):
    if node is null:
        return
    visit(node)
    preorderTraversal(node.left)
    preorderTraversal(node.right)

在上述伪代码中，`visit(node)`表示对节点node的操作，比如打印节点的值。`node.left`和`node.right`分别指向节点的左子节点和右子节点。

对于中序和后序遍历，只需调整访问节点的顺序即可。例如，中序遍历的伪代码如下：

procedure inorderTraversal(node):
    if node is null:
        return
    inorderTraversal(node.left)
    visit(node)
    inorderTraversal(node.right)

### 2.1.2 二叉树的深度和高度计算

二叉树的深度是指从根节点到最远叶子节点的最长路径上的节点数。对于非空二叉树，根节点的深度为1，其左右子树的深度分别为根节点的左右子树的深度加1。二叉树的高度是指从根节点到最远叶子节点的最长路径的边数，与深度的概念相似，只是衡量的单位不同。

递归是计算二叉树深度和高度的自然选择，可以通过递归方法简洁地表达出这一过程。深度和高度的计算可以同时进行，以减少不必要的重复计算。以下是计算二叉树深度和高度的递归函数的伪代码：

function depthAndHeight(node):
    if node is null:
        return (0, 0)
    leftDepth, leftHeight = depthAndHeight(node.left)
    rightDepth, rightHeight = depthAndHeight(node.right)
    depth = 1 + max(leftDepth, rightDepth)
    height = 1 + max(leftHeight, rightHeight)
    return (depth, height)

在上述伪代码中，`depthAndHeight(node)`返回一个包含两个元素的元组，分别表示node为根的子树的深度和高度。如果当前节点为空，那么其深度和高度都是0。否则，递归计算左右子树的深度和高度，并取最大值加1后返回。

## 2.2 递归在图论中的应用

### 2.2.1 深度优先搜索（DFS）

图是另一个重要的数据结构，它由节点（顶点）和连接节点的边组成。图可以用来表示各种复杂的关系和网络。深度优先搜索（DFS）是一种用于图遍历的算法，它沿着图的边进行深入遍历，直到无法继续为止，然后回溯至之前的分叉点继续探索。DFS通常使用递归来实现。

DFS可以用来检测图中是否存在环，寻找两个节点之间的路径，或者对图进行拓扑排序等。以下是DFS算法的伪代码：

procedure DFS(node, visited):
    mark node as visited
    for each neighbor of node:
        if neighbor is not visited:
            DFS(neighbor, visited)

在该伪代码中，`node`是当前正在访问的节点，`visited`是一个标记数组，用来记录哪些节点已经被访问过。对于每个节点，我们将其标记为已访问，然后遍历其所有的邻居。如果邻居节点未被访问过，就递归地对其进行DFS。

### 2.2.2 最短路径问题的解决方法

图论中的另一个重要问题是找到两个节点之间的最短路径，即连接这两个节点的所有路径中边的权重之和最小的路径。最著名的解决最短路径问题的算法是迪杰斯特拉（Dijkstra）算法和贝尔曼-福特（Bellman-Ford）算法。

尽管这些算法主要是通过迭代实现的，但递归也可以用来解决特定类型的图的最短路径问题，特别是在树形图中。递归方法可以简化代码，但通常会有较高的时间和空间复杂度。

例如，如果我们想要计算无权图中节点间的最短路径数，可以使用递归方法：

function countPaths(node, destination, visited):
    if node == destination:
        return 1
    if node in visited:
        return 0
    visited.add(node)
    count = 0
    for each neighbor of node:
        count += countPaths(neighbor, destination, visited)
    visited.remove(node)
    return count

在上述伪代码中，`countPaths`函数计算从`node`到`destination`的路径数量。它递归地计算每一条从当前节点出发到达目标节点的路径数，最后将这些路径数相加起来得到结果。为了避免重复计算相同的路径，使用了一个`visited`集合来跟踪已经访问过的节点。

### 2.2.3 递归算法在图论中的应用示例

对于图的遍历，递归方法特别适合于树形结构的图，例如无环图（DAG）。下面是用Python实现的基于递归的DFS算法，用于遍历图结构：

def DFS(graph, node, visited=None):
    if visited is None:
        visited = set()
    if node not in visited:
        print(node)
        visited.add(node)
        for neighbor in graph[node]:
            DFS(graph, neighbor, visi