C语言递归函数的探索之旅

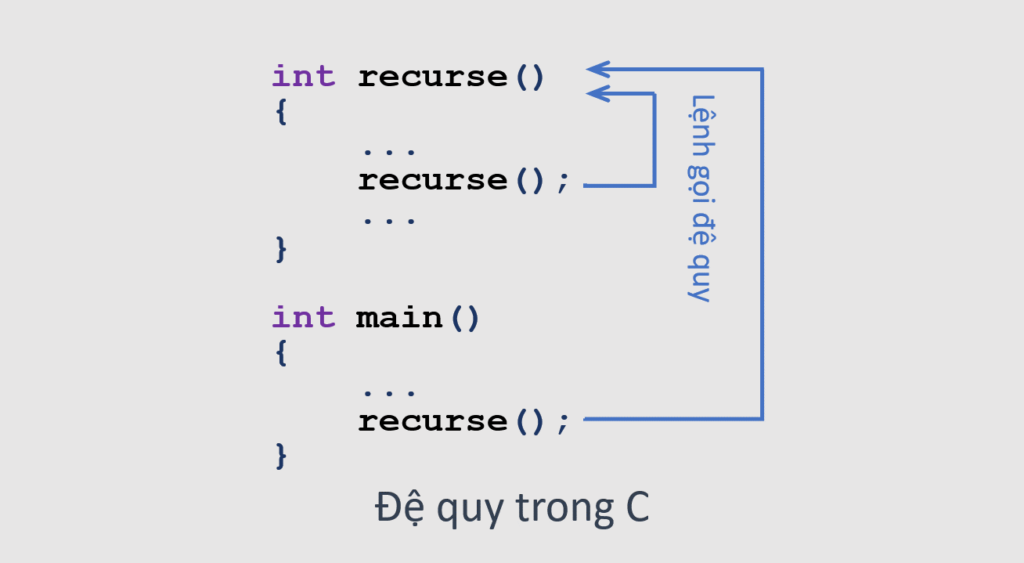
# 1. 递归函数基础理论

## 1.1 递归的定义

在计算机科学中，递归函数是一种调用自己的函数，其基本思想是将大问题分解为小问题，直到问题的规模小到可以轻易解决的程度。递归函数在解决分层数据结构（如树和图）以及可以自然分解为相似子问题的任务中尤其有用。

## 1.2 数学基础

递归函数的数学基础可以在数学归纳法中找到。归纳法由两个步骤组成：基本情况（或基础情况）和归纳步骤。基本情况定义了解决问题的最简单实例，而归纳步骤表明如何使用已解决的较小问题来构建更大问题的解。

## 1.3 递归与迭代的对比

递归和迭代都是算法设计中的基本结构，但它们在实现方法和性能上有所不同。递归通常代码更简洁，易于理解，但在某些情况下可能会导致较大的开销，比如重复计算和过深的调用栈。迭代则是通过循环结构实现，通常比递归更加高效，但也可能导致代码更加复杂。在选择使用哪种方法时，需要权衡代码可读性和性能开销。

在下一章节中，我们将深入了解递归函数在C语言中的原理。

# 2. C语言中递归函数的原理

## 2.1 递归的基本概念

### 2.1.1 递归定义和数学基础

递归函数是编程中的一种常见模式，它允许一个函数直接或间接地调用自身来解决问题。递归的定义通常基于一个简单的数学基础：它是一个分而治之的策略，将大问题分解为小问题，直到达到一个可以直接解决的简单情况（也称为基本情况）。在数学中，递归可以用来定义序列、函数，甚至是整个结构。

例如，一个数列的第n项可以通过前一项或前几项来定义，如著名的斐波那契数列。在编程中，递归函数可以简化为以下形式：

returnType recursiveFunction(parameters) {
    if (终止条件) {
        // 处理基本情况
        return baseCaseResult;
    } else {
        // 分解问题
        returnType partResult = recursiveFunction(modifiedParameters);
        // 合并结果
        return combineResult(partResult);
    }
}

### 2.1.2 递归与迭代的对比

递归和迭代都是解决复杂问题的常见方法，但它们在许多方面有着本质的区别。

- **递归**：在C语言中，递归函数通过函数调用自身来重复执行代码块。递归方法直观、代码简洁，易于理解，但可能带来较高的内存和性能开销，因为每次函数调用都需要额外的内存来存储状态信息。
- **迭代**：迭代是使用循环结构（如`for`或`while`循环）重复执行代码块。迭代方法通常更高效，因为它不需要像递归那样频繁的函数调用和堆栈操作。但是，迭代可能需要更复杂的循环控制逻辑，从而可能降低代码的可读性。

## 2.2 递归函数的工作机制

### 2.2.1 调用栈与递归深度

在C语言中，当一个函数调用另一个函数时，当前函数的执行状态会被保存在一个称为“调用栈”的内存区域中。调用栈跟踪程序中所有的函数调用以及它们的返回地址。每个函数调用都会创建一个新的“栈帧”（stack frame），包含了函数的局部变量、参数和执行上下文。

递归函数会创建一系列嵌套的栈帧，每一层递归调用都会在栈顶添加一个新的栈帧，直至到达基本情况。调用栈的大小受限于系统可用内存，递归深度过大可能导致栈溢出，从而造成程序崩溃。

### 2.2.2 递归终止条件的重要性

递归终止条件是防止无限递归的关键，它确保了递归函数在适当的时候能够停止调用自身。如果没有终止条件，或者终止条件设置不当，递归函数将会无限执行，直到耗尽系统资源。

终止条件通常是一个简单的条件判断，它根据问题的特性和基本情况来设计。例如，在计算阶乘的递归函数中，终止条件是当参数到达0时返回1，因为`n!`在`n=0`时的值为1。

## 2.3 递归函数设计的要点

### 2.3.1 分而治之策略

分而治之是递归函数设计中的一个基本策略，它将一个大问题分解为小问题，然后递归地解决这些小问题，并将结果合并起来得到最终答案。

一个递归函数通常遵循以下模式：

1. 检查基本情况：确定递归何时停止。
2. 分解问题：将大问题分解为小问题。
3. 递归调用：在分解的小问题上递归调用自身。
4. 合并结果：将递归调用返回的结果合并起来得到最终结果。

### 2.3.2 递归树的理解与应用

递归树是一个形象化的工具，可以帮助我们理解递归函数的工作过程。它通过树形结构展示函数的调用过程，其中每个节点代表函数的一次调用，子节点代表函数对子问题的递归调用。

例如，在计算斐波那契数列的递归函数中，一个节点可能代表`F(4)`的计算，其左子节点代表`F(3)`的计算，右子节点代表`F(2)`的计算，而`F(3)`的右子节点又会进一步分解为`F(1)`和`F(0)`的计算。

递归树可以帮助我们识别哪些部分是重复的，从而识别可能的优化点，例如使用缓存（memoization）技术来避免重复计算。

以上是第二章“C语言中递归函数的原理”的详细内容，通过细致的分析与举例，我们不仅了解了递归函数的定义和特性，还深入探讨了递归的工作机制，学习了递归函数设计的重要要点，并用树形结构进行了直观的理解。这一章节为理解递归在实际编程中的应用打下了坚实的基础。

# 3. C语言递归函数实例剖析

在C语言编程中，递归函数是一个非常强大的工具，它允许函数调用自身来解决问题。递归通常用于解决可以分解为更小相似问题的任务。在本章中，我们将通过具体实例来深入了解递归函数如何在C语言中实现，并展示其在解决各种问题时的有效性和优雅性。

## 3.1 简单递归函数应用

### 3.1.1 计算阶乘

阶乘函数是递归函数的一个典型入门级应用。在数学中，n的阶乘（记为n!）是所有小于或等于n的正整数的乘积。例如，5! = 5 × 4 × 3 × 2 × 1 = 120。利用递归，我们可以定义阶乘函数如下：

#include <stdio.h>

// 函数声明
unsigned long long factorial(int n);

int main() {
    int number;
    printf("Enter a positive integer: ");
    scanf("%d", &number);
    printf("Factorial of %d = %llu\n", number, factorial(number));
    return 0;
}

// 计算阶乘的递归函数实现
unsigned long long factorial(int n) {
    if (n >= 1) {
        return n * factorial(n - 1); // 递归调用
    } else {
        return 1; // 递归终止条件
    }
}

在上述代码中，`factorial`函数通过递归调用自身来计算阶乘。如果`n`为1或更小，递归终止并返回1，否则递归继续直到达到这个基本情况。

### 3.1.2 斐波那契数列

斐波那契数列是一个经典的递归问题。数列中的每一个数都是前两个数的和，通常从0和1开始。斐波那契数列的前几个数字是0, 1, 1, 2, 3, 5, 8, ...

#include <stdio.h>

// 函数声明
long long fibonacci(int n);

int main() {
    int n;
    printf("Enter a positive integer: ");
    scanf("%d", &n);
    printf("Fibonacci number of %d = %lld\n", n, fibonacci(n));
    return 0;
}

// 斐波那契数列的递归实现
long long fibonacci(int n) {
    if (n <= 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        return fibonacci(n - 1) + fibonacci(n - 2); // 递归调用
    }
}

斐波那契数列的递归实现虽然简单明了，但效率很低，特别是对于较大的`n`值。每次调用`fibonacci`函数时都会计算`fibonacci(n - 1)`和`fibonacci(n - 2)`，这会导致大量的重复计算。

## 3.2 复杂问题的递归解法

### 3.2.1 汉诺塔问题

汉诺塔问题是一个经典的递归问题，要求玩家将一系列大小不一的盘子从一个塔座移动到另一个塔座上，且每次只能移动一个盘子，且大盘子不能放在小盘子上面。该问题的递归解法如下：

#include <stdio.h>

// 函数声明
void hanoi(int n, char from_rod, char to_rod, char aux_rod);

int main() {
    int n = 3; // 盘子数量
    hanoi(n, 'A', 'C', 'B'); // A、B、C为塔座名称
    return 0;
}

// 汉诺塔的递归解决方案
void hanoi(int n, char from_rod, char to_rod, char aux_rod) {
    if (n == 1) {
        printf("Move disk 1 from rod %c to rod %c\n", from_rod, to_rod);
        return;
    }
    hanoi(n - 1, from_rod, aux_rod, to_rod);
    printf("Move disk %d from rod %c to rod %c\n", n, from_rod, to_rod);
    hanoi(n - 1, aux_rod, to_rod, from_rod);
}

汉诺塔的递归解法很优雅，每一步移动都遵循着递归的思路：把问题分解成更小的子问题来解决。

### 3.2.2 排序算法中的递归实现

递归也可用于实现各种排序算法，例如快速排序和归并排序。这里以快速排序为例，其思想是选取一个基准值（pivot），将数组分为两部分，一部分小于基准值，另一部分大于基准值，然后对这两部分再递归地进行快速排序。

#include <stdio.h>

// 函数声明
void quickSort(int arr[], int low, int high);
int partition(int arr[], int low, int high);
void swap(int* a, int* b);

int main() {
    int arr[] = {10, 7, 8, 9, 1, 5};
    int n = sizeof(arr) / sizeof(arr[0]);
    quickSort(arr, 0, n - 1);
    printf("Sorted array: \n");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return 0;
}

// 快速排序函数实现
void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

// 分区函数
int partition(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = (low - 1);
    for (int j = low; j <= high - 1; j++) {
        if (arr[j] < pivot) {
            i++;
            swap(&arr[i], &arr[j]);
        }
    }
    swap(&arr[i + 1], &arr[high]);
    return (i + 1);
}

// 交换两个元素
void swap(int* a, int* b) {
    int t = *a;
    *a = *b;
    *b = t;
}

快速排序的递归实现非常高效，但是它的性能依赖于基准值的选择。

## 3.3 递归与动态规划

### 3.3.1 动态规划简介

动态规划是解决复杂问题的一种方法，通过把问题分解成一系列重叠的子问题，并使用记忆化方法来避免重复计算。动态规划通常与递归配合使用，但它可以避免递归中的一些缺陷，比如重复计算和高时间复杂度。

### 3.3.2 递归与动态规划的结合

在某些问题中，递归函数和动态规划可以结合使用来提高效率。以斐波那契数列为例，我们可以使用记忆化来避免重复计算，代码如下：

#include <stdio.h>
#include <string.h>

#define N 1000

// 函数声明
long long fibonacci_memoized(int n);

int main() {
    int n = 40; // 大数值计算
    printf("Fibonacci number of %d = %lld\n", n, fibonacci_memoized(n));
    return 0;
}

// 使用记忆化的斐波那契数列
long long fibonacci_memoized(int n) {
    long long fib[N];
    memset(fib, 0, sizeof(fib));
    fib[1] = 1;
    for (int i = 2; i <= n; i++) {
        fib[i] = fib[i - 1] + fib[i - 2];
    }
    return fib[n];
}

在上述代码中，我们使用数组`fib`来存储计算过的斐波那契数，从而避免了递归中的重复计算。这种优化后的递归方法被称为记忆化递归，它结合了递归和动态规划的优点。

以上为第三章：C语言递归函数实例剖析的内容，涵盖了递归函数在简单问题和复杂问题中的应用，以及递归与动态规划的结合。接下来，我们将探讨递归函数的优化与调试。

# 4. 递归函数的优化与调试

## 4.1 递归深度的限制与优化
在使用递归解决问题时，不可避免地会遇到递归深度的问题。随着递归调用次数的增加，系统开销也会随之增加。因此，合理地限制递归深度，并采取适当的优化策略是十分必要的。

### 4.1.1 递归深度过大的问题与解决
当递归深度过大时，可能会引发栈溢出错误（Stack Overflow），尤其是当系统默认的栈空间不足以满足程序需求时。为了应对这种情况，我们可以通过增加栈空间来暂时缓解问题。例如，在GCC编译器中，可以使用 `-Wl,--stack,N` 选项来设置栈空间大小（N 为字节数）。

然而，增加栈空间并非长久之计，更合理的解决方法是优化递归算法，减少递归调用的深度。例如，在递归函数中使用循环来代替某些递归调用，或者采用尾递归优化等技术。

### 4.1.2 尾递归优化技巧
尾递归是一种特殊的递归形式，在函数的最后一步操作是调用自身时使用。编译器对尾递归的优化可以将递归转化为迭代，有效减少递归深度。下面是一个尾递归的例子：

int factorial(int n, int accumulator) {
    if (n == 0) {
        return accumulator;
    }
    return factorial(n-1, n * accumulator);
}

int main() {
    printf("%d\n", factorial(5, 1)); // 输出 120
    return 0;
}

在这个阶乘函数中，`accumulator` 参数作为累加器，保存了阶乘的中间结果。当 `n` 为0时，函数返回累加器的值，这是尾调用的情况。在某些编译器中，如GCC，如果开启了优化选项 `-O2`，则会自动对尾递归进行优化。

## 4.2 递归函数的调试技巧
在调试递归函数时，需要理解递归调用的过程和栈的使用方式。这通常是困难的，因为涉及到多次函数调用和多个函数实例同时存在的情况。

### 4.2.1 使用调试工具理解递归调用
现代IDE和调试工具提供了强大的功能来帮助开发者理解递归调用。大多数调试器支持步进（step into）、步出（step out）、继续（continue）等操作，并能显示当前的调用栈。

以GDB为例，可以使用 `backtrace` 命令来查看当前调用栈的状态：

(gdb) backtrace
#0  factorial (n=5, accumulator=1) at main.c:10
#1  0x0000000000400546 in main () at main.c:22

这将显示从当前函数调用到最顶层调用的堆栈追踪信息。另外，可以设置断点在特定的递归深度，来观察和调试。

### 4.2.2 常见递归错误的排除
递归函数中常见的错误包括无限递归、递归终止条件不正确等。通过在递归调用前后输出日志信息，或者使用调试器的条件断点功能，可以帮助定位问题。

例如，对于无限递归的错误，可以设置一个断点在递归函数的开始，并在调试器中检查是否满足退出条件。

## 4.3 非递归算法的探索
尽管递归提供了一种直观且强大的解决问题的方法，但在一些情况下，非递归（迭代）算法更为高效和安全。

### 4.3.1 非递归算法的优势与应用场景
非递归算法通常比递归算法使用更少的内存资源，因为它们不涉及系统调用栈的消耗。此外，非递归算法更容易理解，对于编译器优化来说也更加友好。

一种常见的非递归算法是使用堆栈数据结构来模拟递归过程。这种方式可以完全避免递归调用，从而避免栈溢出的风险。

下面是一个使用堆栈来模拟计算阶乘的非递归实现：

#include <stdio.h>
#include <stdlib.h>

typedef struct StackNode {
    int data;
    struct StackNode *next;
} StackNode;

typedef struct {
    StackNode *top;
} Stack;

void initStack(Stack *stack) {
    stack->top = NULL;
}

int isEmpty(Stack *stack) {
    return stack->top == NULL;
}

void push(Stack *stack, int data) {
    StackNode *node = (StackNode*)malloc(sizeof(StackNode));
    node->data = data;
    node->next = stack->top;
    stack->top = node;
}

int pop(Stack *stack) {
    if (isEmpty(stack)) {
        return -1;
    }
    StackNode *topNode = stack->top;
    int data = topNode->data;
    stack->top = topNode->next;
    free(topNode);
    return data;
}

int factorial(int n) {
    Stack stack;
    initStack(&stack);
    int result = 1;
    while (n > 0) {
        push(&stack, n);
        n--;
    }
    while (!isEmpty(&stack)) {
        result *= pop(&stack);
    }
    return result;
}

int main() {
    printf("%d\n", factorial(5)); // 输出 120
    return 0;
}

在这个例子中，我们通过一个栈数据结构来模拟递归调用过程。通过这种方式，我们可以避免递归深度过大的问题。

### 4.3.2 将递归算法转换为非递归实现
将递归算法转换为非递归实现需要我们理解原始递归算法的工作原理，并找到一种迭代的方式来代替。有时候，这个过程并不简单，特别是在涉及到复杂的递归逻辑时。

对于简单的递归算法，转换通常涉及到使用循环结构和栈、队列等数据结构来存储中间状态。而对于复杂的递归算法，可能需要更加深入的算法设计和数学分析。

例如，考虑以下简单的递归函数：

int recursiveFunction(int n) {
    if (n <= 1) {
        return n;
    }
    return recursiveFunction(n - 1) + recursiveFunction(n - 2);
}

该函数模拟了斐波那契数列的计算，它是一个典型的递归调用模型。将其转换为非递归形式，我们可以使用一个循环来代替递归调用，并用两个变量来保存中间结果，从而避免递归深度过大的问题。

通过本章节的介绍，我们了解到递归函数深度的限制与优化方法，掌握了递归函数调试技巧，探讨了非递归算法的实现方式。这些内容为我们编写更加高效和稳定的递归程序打下了坚实的基础。

# 5. 递归函数的高级应用

递归函数不仅在基础理论和常规应用中有着重要的地位，而且在处理复杂数据结构和解决特定领域问题时，它同样展现出了强大的能力。高级应用展示了递归如何被用于实现树形结构的递归遍历、算法竞赛中的递归解法以及图论中的递归算法。

## 5.1 树形结构与递归遍历

树形结构是计算机科学中的一种基础数据结构，二叉树是一种特殊的树形结构，递归遍历算法是处理二叉树的基础方法之一。而N叉树作为树形结构的一种扩展，其递归遍历的逻辑与二叉树类似，但在具体实现时存在差异。

### 5.1.1 二叉树的递归遍历算法

二叉树的递归遍历主要包括三种方式：前序遍历、中序遍历和后序遍历。每种遍历方式都有其特定的应用场景和数据处理顺序。

**前序遍历**

在前序遍历中，我们首先访问根节点，然后递归地遍历左子树，最后递归地遍历右子树。

void preOrderTraversal(TreeNode* root) {
    if (root == NULL) return;
    visit(root); // 访问根节点
    preOrderTraversal(root->left); // 遍历左子树
    preOrderTraversal(root->right); // 遍历右子树
}

**中序遍历**

在中序遍历中，我们先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。

void inOrderTraversal(TreeNode* root) {
    if (root == NULL) return;
    inOrderTraversal(root->left); // 遍历左子树
    visit(root); // 访问根节点
    inOrderTraversal(root->right); // 遍历右子树
}

**后序遍历**

在后序遍历中，我们先递归地遍历左子树，然后递归地遍历右子树，最后访问根节点。

void postOrderTraversal(TreeNode* root) {
    if (root == NULL) return;
    postOrderTraversal(root->left); // 遍历左子树
    postOrderTraversal(root->right); // 遍历右子树
    visit(root); // 访问根节点
}

在上述代码中，`visit(root)`是一个假设的函数，用于处理访问到的节点。实际使用时应根据具体需求进行定义。

### 5.1.2 N叉树与递归

与二叉树类似，N叉树的递归遍历需要遍历每个节点的所有子节点。由于N叉树的子节点数量不固定，所以递归方法需要进行调整以适应这种结构。

void NaryTreeTraversal(Node* root) {
    if (root == NULL) return;
    for (int i = 0; i < root->childrenCount; ++i) {
        NaryTreeTraversal(root->children[i]); // 递归遍历每个子节点
    }
    visit(root); // 访问当前节点
}

在上述代码中，`Node`结构体代表了一个N叉树节点，它有一个`children`数组用于存储子节点，`childrenCount`用于记录子节点的数量。

## 5.2 递归函数在算法竞赛中的应用

在算法竞赛中，递归的应用非常广泛。递归思想能够帮助参赛者以更直观的方式理解问题，并设计出简洁优雅的解法。

### 5.2.1 组合数学问题的递归解法

组合数学问题经常可以用递归的方式来解决，特别是在涉及到排列组合的选择时，递归能够很自然地模拟出选择的过程。

int combination(int n, int k) {
    if (k == 0 || k == n) return 1; // 终止条件
    return combination(n - 1, k - 1) + combination(n - 1, k);
}

在这个例子中，我们用递归方式实现了组合数的计算。该公式基于组合数的性质：C(n, k) = C(n-1, k-1) + C(n-1, k)，这是组合数学中的一个经典递归关系。

### 5.2.2 递归在算法竞赛中的典型问题

另一个典型问题是在算法竞赛中经常出现的汉诺塔问题。递归算法可以简洁地解决这个问题，递归方法的优雅使得它在许多编程竞赛中受到青睐。

void hanoi(int n, char from_rod, char to_rod, char aux_rod) {
    if (n == 1) {
        printf("\nMove disk 1 from rod %c to rod %c", from_rod, to_rod);
        return;
    }
    hanoi(n - 1, from_rod, aux_rod, to_rod);
    printf("\nMove disk %d from rod %c to rod %c", n, from_rod, to_rod);
    hanoi(n - 1, aux_rod, to_rod, from_rod);
}

在这个汉诺塔问题中，我们需要将n个盘子从`from_rod`移动到`to_rod`，使用`aux_rod`作为辅助。递归调用分为两个步骤：首先将上面的n-1个盘子移动到辅助柱子上，然后将最大的盘子移动到目标柱子上，最后将n-1个盘子从辅助柱子移动到目标柱子上。

## 5.3 图论中的递归算法

图论是计算机科学中的重要领域，它广泛应用于网络、社交关系、交通路线等。深度优先搜索(DFS)是图论中一个基础的搜索算法，它利用递归实现了图的深度优先遍历。

### 5.3.1 深度优先搜索(DFS)的递归实现

深度优先搜索通过递归的方式从图的一个未被访问的节点开始探索，直到路径的末端，然后回溯到上一个节点，探索其他路径。

void DFSUtil(Graph* graph, int v, bool visited[]) {
    visited[v] = true;
    printNode(v); // 标记当前节点为已访问并处理节点数据

    // 递归访问所有未被访问的邻接节点
    for (int i = 0; i < graph->numberOfVertices; ++i) {
        if (isAdjacent(graph, v, i) && !visited[i]) {
            DFSUtil(graph, i, visited);
        }
    }
}

在这个DFS的实现中，`Graph`结构体代表了图，`visited`数组用于记录每个节点是否被访问过。

### 5.3.2 递归在解决图论问题中的作用

递归在图论问题中的作用非常广泛，除了DFS之外，递归还可以用于其他图论算法，如拓扑排序、生成树算法等。递归方法能够将复杂的问题简化为更小的、更易于管理的子问题。

递归函数的高级应用是其能力的集中展现，无论是在数据结构的深入理解上，还是在算法竞赛中快速寻找解决方案，亦或是在图论中的深层次应用，递归都显示了其在复杂问题解决中的独特优势。通过这一章节的学习，读者应能深刻理解递归在实际应用中的多样性和高效性，并能在不同场景下灵活运用递归思想。

# 6. 递归思想的其他领域扩展

## 6.1 递归思想在函数式编程中的应用

递归思想在函数式编程中占据着核心地位，因为函数式编程强调不可变性和无副作用的函数。在这样的范式下，递归提供了一种自然的迭代方式。

### 6.1.1 函数式编程简介

函数式编程是一种编程范式，它将计算视为数学函数的评估，并避免改变状态和可变数据。这与命令式编程形成鲜明对比，后者依赖于改变程序状态。

函数式编程的语言特性包括高阶函数、不可变数据结构、函数作为一等公民等。这些特性使得递归成为函数式编程中最常用的迭代方法之一。

### 6.1.2 递归与高阶函数的结合

高阶函数是至少满足下列一个条件的函数：接受一个或多个函数作为输入，或输出一个函数。在函数式编程中，递归经常与高阶函数如 `map`、`reduce` 或 `filter` 结合使用。

例如，在 JavaScript 中使用递归与 `reduce` 函数来计算数组的总和：

function recursiveSum(array) {
    if (array.length === 0) {
        return 0;
    } else {
        return array[0] + recursiveSum(array.slice(1));
    }
}

const result = recursiveSum([1, 2, 3, 4, 5]); // 结果为15

在这个例子中，`recursiveSum` 函数使用 `slice` 方法来创建一个新的数组，然后将第一个元素与对剩余部分调用 `recursiveSum` 的结果相加，这是一种典型的尾递归。

## 6.2 递归与人工智能

递归在人工智能领域内有许多应用，尤其是在那些需要深度搜索和问题求解的任务中。

### 6.2.1 递归在人工智能算法中的作用

递归在人工智能算法中的作用可以体现在多个层面上。例如，在搜索算法中，递归能够实现树状或图状搜索空间的深度优先遍历。递归方法在许多决策树算法中也很常见。

递归在基于规则的专家系统中也是重要的，它们通常使用规则的递归应用来推导结论。

### 6.2.2 递归在自然语言处理中的应用实例

在自然语言处理（NLP）中，递归可以被用在语言模型、语法分析以及句子结构的解析中。例如，在解析句子语法结构时，递归下降解析器是一种简单高效的实现方式。

递归下降解析器是根据语法规则递归地对输入的字符串进行解析。每当识别出一个语法规则，它就将对应的子串传递给下一个递归调用，直至整个句子被解析完毕。

## 6.3 递归的哲学与思考

递归不仅是一种编程技术，它还反映了自然界和人类思考中的某些普遍性原则。

### 6.3.1 递归与自我相似性

递归与自然界中的自我相似性现象相呼应。例如，雪花的结构、树枝的分布、山脉的轮廓等，都以递归的形式展现。这种自相似性在分形几何中得到了很好的体现。

在编程中，这种自相似性可以反映在递归数据结构上，如链表、二叉树等。

### 6.3.2 递归思想对编程思维的影响

递归思想对编程思维的影响深远。它教会我们如何将复杂问题分解为更小的子问题，直到达到可以直接解决的程度。这种分解过程不仅限于编写递归代码，它也是设计复杂系统和解决困难问题的一种通用方法。

例如，当我们需要编写一个算法来解决一个看似困难的问题时，我们可以尝试定义问题的子问题，然后解决这些子问题，并将它们组合起来得到最终的解决方案。

递归思想让我们能够从更高层次去理解和思考问题，避免陷入具体的细节中，这在编程和算法设计中是极其宝贵的。