机器学习精确率深度剖析：指标解读与提升方法大公开

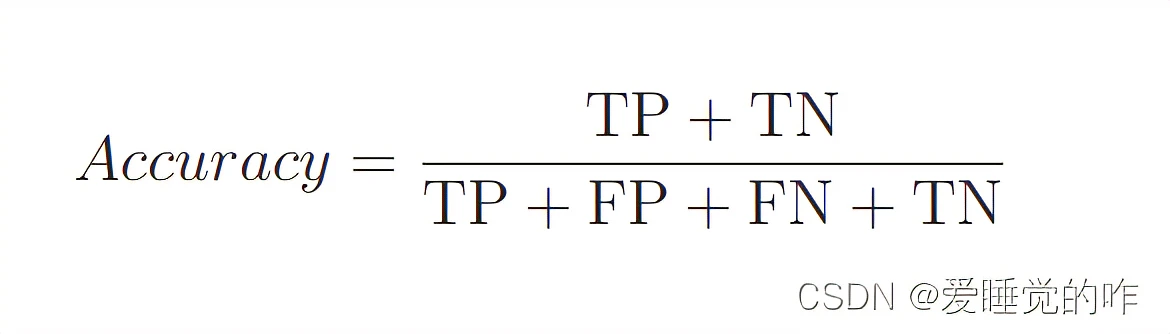
# 1. 精确率的定义和重要性

精确率（Precision）是衡量模型在预测为正例中实际为正例的比例，它关注的是模型对正类预测的准确性。在信息检索、分类问题、自然语言处理等众多应用中，精确率是衡量模型性能的关键指标之一。良好的精确率意味着模型在识别出的正例中，错误标记的反例较少，这对于减少后续处理工作量、提高决策质量有着不可或缺的作用。在不同领域，如医疗诊断、金融欺诈检测等，精确率的重要性愈发凸显，因为它们直接关联到风险控制和资源利用的效率。

# 2. 精确率与其他评估指标的关系

精确率是评估机器学习模型性能的关键指标之一，但要全面评估模型，我们还需要考虑其他指标，如召回率、准确率，以及F1分数等。这些指标与精确率共同构成一个完整的评估体系，帮助我们从不同角度理解模型的表现。

### 2.1 精确率与召回率的平衡

精确率（Precision）和召回率（Recall）是衡量分类模型性能的两个重要指标，它们在信息检索和分类问题中特别重要。

#### 2.1.1 精确率-召回率曲线

精确率-召回率曲线（Precision-Recall Curve）是一个图形化工具，用于展示模型在不同阈值下的精确率和召回率。该曲线越靠近左上角，表示模型性能越好。如下是一个使用Python中`sklearn`库绘制的示例代码，展示如何生成并绘制PR曲线。

import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import PrecisionRecallDisplay

# 假设y_true是真实的标签，y_scores是模型预测的置信度分数
y_true = [0, 0, 1, 1]
y_scores = [0.1, 0.4, 0.35, 0.8]

precision, recall, thresholds = precision_recall_curve(y_true, y_scores)

# 绘制精确率-召回率曲线
display = PrecisionRecallDisplay(precision=precision, recall=recall).plot()
plt.show()

#### 2.1.2 F1分数：精确率和召回率的调和平均

F1分数是精确率和召回率的调和平均，它提供了一个介于精确率和召回率之间的单一数值指标，有助于在两者之间进行平衡。F1分数的计算公式为：

F1 = 2 * (Precision * Recall) / (Precision + Recall)

下面是一个计算F1分数的Python代码示例：

from sklearn.metrics import f1_score

# 假设y_true是真实的标签，y_pred是模型的预测结果
y_true = [1, 1, 0, 1, 0]
y_pred = [1, 0, 0, 1, 1]

# 计算F1分数
f1 = f1_score(y_true, y_pred, average='binary')
print("F1 Score:", f1)

### 2.2 精确率与准确率的区别

精确率和准确率虽然都用来衡量模型的性能，但它们关注的焦点不同。

#### 2.2.1 准确率的定义及其局限性

准确率（Accuracy）是模型预测正确的样本数占总样本数的比例，公式为：

Accuracy = (True Positives + True Negatives) / (Total Samples)

准确率的一个局限性在于，在类别不均衡的数据集中，即使模型对多数类预测很差，准确率也可能很高，因此它无法充分反映模型的真实性能。

#### 2.2.2 精确率与准确率在不同场景的应用

在特定的业务场景中，精确率和准确率的应用需求会有所不同。例如，若错误的预测可能造成严重后果，如医疗诊断，精确率通常比准确率更重要。

### 2.3 精确率在多类分类问题中的考量

在多类分类问题中，精确率的考量更为复杂。

#### 2.3.1 微平均、宏平均与加权平均

多类分类问题中，精确率的计算可以考虑微平均、宏平均或加权平均。

- 微平均（Micro-Averaged）: 混合所有的样本，计算全局的精确率。
- 宏平均（Macro-Averaged）: 分别计算每个类别的精确率，然后求平均。
- 加权平均（Weighted-Averaged）: 根据每个类别的样本数量进行加权。

#### 2.3.2 多类分类中精确率的挑战与应对

在多类分类问题中，不同类别的样本数量可能存在巨大差异，这会对精确率的计算产生影响。一个有效的解决策略是使用带权重的精确率计算方法。

例如，我们可以用以下公式来计算多类分类问题中的加权精确率：

Weighted Precision = Σ(W_c * Precision_c) / ΣW_c

其中，`W_c`是类别c的权重，`Precision_c`是类别c的精确率。

在实际应用中，根据数据集的不同，可能需要采用不同的策略来处理精确率的计算。

以上就是第二章关于精确率与其他评估指标关系的详细解读。在后续的章节中，我们将深入探讨精确率的计算方法、优化策略及其在不同行业中的应用。

# 3. 精确率的计算方法与实践

精确率（Precision）是信息检索和机器学习领域评价分类系统性能的一个关键指标。它衡量的是在被模型判定为正例的样本中，实际为正例的比例。本章深入探讨精确率的计算方法，并提供实际操作的示例代码，以便读者更好地理解精确率的含义和应用。

## 3.1 精确率的直接计算公式

精确率的计算公式相对简单，可以用下面的公式表示：

\[ \text{精确率} = \frac{真正例（TP）}{真正例（TP）+ 假正例（FP）} \]

其中，真正例（True Positives，TP）指的是模型正确预测为正类的样本数，而假正例（False Positives，FP）是模型错误地预测为正类的样本数。

## 3.2 精确率的实现代码（Python示例）

为了更好地理解精确率的计算，接下来将通过Python代码示例进行演示。这里我们将使用Python中最流行的机器学习库之一：scikit-learn。

### 3.2.1 利用scikit-learn计算精确率

首先，导入必要的库和数据集：

from sklearn.metrics import precision_score
from sklearn.datasets import make_classification

# 生成一个模拟的分类数据集
X, y = make_classification(n_samples=1000, n_features=20, n_informative=2, n_redundant=10, random_state=42)

# 假设我们有一个简单的分类器，将所有的样本都预测为类别0
y_pred = [0]*len(y)

然后，使用`precision_score`函数计算精确率：

precision = precision_score(y, y_pred)
print(f'精确率: {precision}')

在上面的代码中，我们创建了一个1000个样本的数据集