C++动态数组的高级排序、搜索和插入技巧

# 1. C++动态数组概述

在现代C++程序设计中，动态数组是一种常用的数据结构，提供了灵活的数据存储能力。它允许开发者在运行时决定数组的大小，并且可以根据需要动态地扩展或缩减数组长度。与静态数组相比，动态数组的优势在于其更好的内存管理和扩展性，让开发者能够在内存使用和性能上做出更加精细的调整。

## 动态数组的基本原理

在C++中，动态数组通常是通过指针和内存分配函数（如`new`和`delete`）来实现的。通过这些操作符，程序员能够在堆内存上动态地分配和释放数组空间。动态数组的大小可以在编译时不确定，而是在程序运行时通过程序逻辑确定。

## 动态数组的优势与用途

动态数组特别适用于以下情况：
- 数据数量未知或在运行时变化时
- 当需要优化内存使用，避免静态数组的浪费时
- 在构建复杂的数据结构，如图、树等时，动态分配子结构的空间

int *arr = new int[n]; // 在堆上分配n个整型元素的空间
delete[] arr; // 使用完毕后释放空间

在上述代码中，`n`可以是任意正整数，意味着数组`arr`的大小仅受限于机器内存的大小。这种灵活性是静态数组所不具备的，同时也意味着程序员需要更小心地处理内存泄漏和边界检查等问题。在下一章，我们将深入探讨动态数组的高级排序技术，以提高数据处理的效率。

# 2. 动态数组的高级排序技术的第二节内容，即"实现快速排序和归并排序"。按照指示，这将是一个独立的内容模块，从"2.2 实现快速排序和归并排序"开始，到"2.2.2 归并排序的原理与实现"结束，以满足内容的连贯性和深度。

## 2.2 实现快速排序和归并排序

### 2.2.1 快速排序的原理与实现

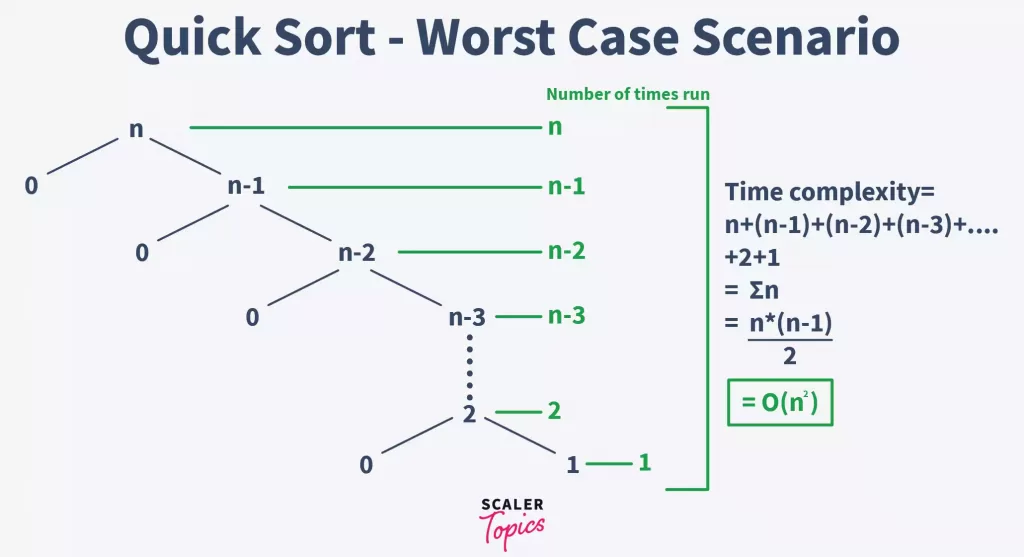
快速排序（Quick Sort）是一种高效的排序算法，通过选择一个“基准值”（pivot），将待排序数组分为两个子数组，一个子数组的所有数据都比另一个子数组的所有数据小，然后递归地对这两个子数组进行快速排序。快速排序算法的平均时间复杂度为O(n log n)，但最坏情况下会退化为O(n^2)。

下面展示快速排序的一个基本实现：

#include <iostream>
#include <vector>
using namespace std;

void swap(int &a, int &b) {
    int temp = a;
    a = b;
    b = temp;
}

int partition(vector<int> &arr, int low, int high) {
    int pivot = arr[high]; // pivot
    int i = (low - 1); // Index of smaller element and indicates the right position of pivot found so far

    for (int j = low; j <= high - 1; j++) {
        // If current element is smaller than the pivot
        if (arr[j] < pivot) {
            i++; // increment index of smaller element
            swap(arr[i], arr[j]);
        }
    }
    swap(arr[i + 1], arr[high]);
    return (i + 1);
}

void quickSort(vector<int> &arr, int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

int main() {
    vector<int> arr = {10, 7, 8, 9, 1, 5};
    int n = arr.size();
    quickSort(arr, 0, n - 1);
    cout << "Sorted array: \n";
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
    cout << "\n";
    return 0;
}

在上述代码中，`partition` 函数是快速排序的核心，负责划分数组。`quickSort` 函数是递归函数，用于对数组的子区段进行排序。

#### 快速排序的时间复杂度分析

快速排序的平均时间复杂度为O(n log n)，在大多数情况下快速排序都能达到这个效率。然而，如果每次选取的基准值都是最小或最大值，快速排序的时间复杂度会退化到O(n^2)。为了避免这种最坏情况的发生，通常会采用随机化基准值的选择方法，或者使用三数取中法（选择最左、最右和中间三个值的中位数作为基准值）。

### 2.2.2 归并排序的原理与实现

归并排序（Merge Sort）是一种分治算法，它将数组分成两半，分别对这两半递归地应用归并排序，然后将结果合并起来。归并排序的合并过程是它最独特的地方，它将两个已排序的数组合并成一个有序数组。归并排序的时间复杂度为O(n log n)，且它是稳定的排序算法。

下面展示归并排序的基本实现：

#include <iostream>
#include <vector>
using namespace std;

void merge(vector<int> &arr, int const left, int const mid, int const right) {
    auto const subArrayOne = mid - left + 1;
    auto const subArrayTwo = right - mid;

    // 创建临时数组
    vector<int> leftArray(subArrayOne), rightArray(subArrayTwo);

    // 复制数据到临时数组
    for (auto i = 0; i < subArrayOne; i++)
        leftArray[i] = arr[left + i];
    for (auto j = 0; j < subArrayTwo; j++)
        rightArray[j] = arr[mid + 1 + j];

    auto indexOfSubArrayOne = 0, // 初始索引归并左边子数组
        indexOfSubArrayTwo = 0; // 初始索引归并右边子数组
    int indexOfMergedArray = left; // 初始索引合并后的临时数组

    // 合并临时数组回原数组
    while (indexOfSubArrayOne < subArrayOne && indexOfSubArrayTwo < subArrayTwo) {
        if (leftArray[indexOfSubArrayOne] <= rightArray[indexOfSubArrayTwo]) {
            arr[indexOfMergedArray] = leftArray[indexOfSubArrayOne];
            indexOfSubArrayOne++;
        } else {
            arr[indexOfMergedArray] = rightArray[indexOfSubArrayTwo];
            indexOfSubArrayTwo++;
        }
        indexOfMergedArray++;
    }
    // 复制剩余元素
    while (indexOfSubArrayOne < subArrayOne) {
        arr[indexOfMergedArray] = leftArray[indexOfSubArrayOne];
        indexOfSubArrayOne++;
        indexOfMergedArray++;
    }
    while (indexOfSubArrayTwo < subArrayTwo) {
        arr[indexOfMergedArray] = rightArray[indexOfSubArrayTwo];
        indexOfSubArrayTwo++;
        indexOfMergedArray++;
    }
}

void mergeSort(vector<int> &arr, int const begin, int const end) {
    if (begin