【K-means在图像处理中的威力】：图像分割与特征提取的实践技术


参考资源链接：[K-means聚类算法详解及应用](https://wenku.csdn.net/doc/2fg9jjg6qn?spm=1055.2635.3001.10343)
# 1. K-means算法概述

K-means算法是数据分析和机器学习中常用的聚类方法，属于无监督学习算法。它的基本原理是通过迭代计算，将数据集中的样本点划分到K个簇中，使得每个样本点属于使其自身与簇中心距离之和最小的簇。

## 1.1 K-means算法简介

K-means算法由J. MacQueen在1967年提出，旨在解决将数据集分割为K个簇的问题，使得每个簇内的数据点尽量紧密，而簇间的距离尽量远离。该算法简单高效，在处理大规模数据集时尤其具有优势。

## 1.2 算法优势

K-means算法的优势在于其计算效率高，易于理解和实现。它不需要预先设定分类标签，通过优化目标函数直接对数据进行聚类。然而，K-means算法也有其局限性，如对初始质心的选择敏感，对簇形状和大小的假设严格等。

## 1.3 算法应用场景

由于K-means的这些特点，它被广泛应用于市场细分、图像分割、社交网络分析、文档聚类等领域。在这些应用场景中，K-means算法都能根据数据的自然分布将数据合理地划分为多个类别。

# 2. 图像分割中的K-means应用

## 2.1 K-means算法原理
### 2.1.1 算法初始化与核心思想

K-means算法是一种经典的聚类算法，广泛应用于数据挖掘、图像处理等领域。其核心思想是将n个数据点划分为k个簇，使得簇内的数据点之间的相似度尽可能高，而不同簇内的数据点之间的相似度尽可能低。

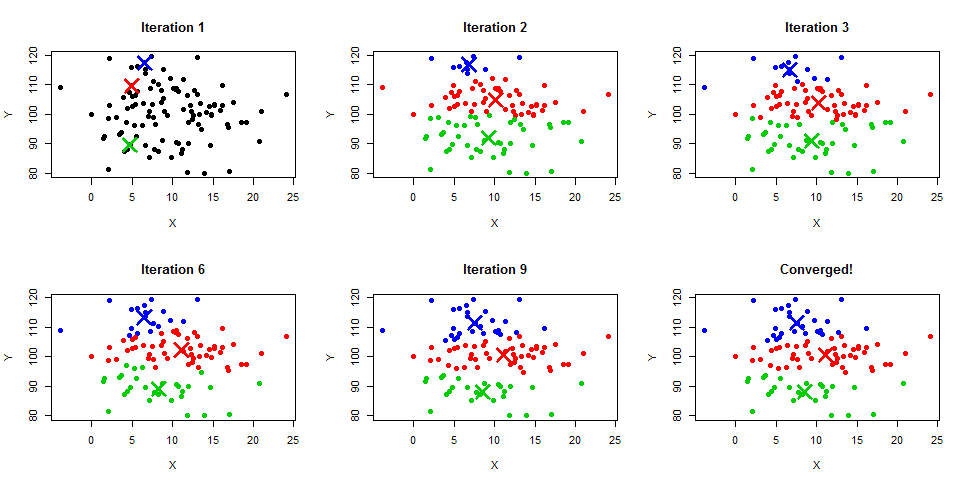
在初始化阶段，K-means算法通常采用随机方式选择k个数据点作为初始质心。随后，算法进入迭代过程，根据数据点与质心的距离，将每个数据点划分到距离最近的质心所代表的簇中。接着，对每个簇中的数据点重新计算质心，即求出簇内所有点的均值位置。这一过程不断重复，直到质心不再发生显著变化或者达到预设的迭代次数为止。

### 2.1.2 距离度量与聚类过程

距离度量是K-means算法中关键的一环，它决定了数据点如何被分配到最近的质心。常用的度量方法有欧氏距离、曼哈顿距离等。不同的距离度量方法会影响最终的聚类结果。

聚类过程主要由两部分组成：分类和更新。在分类步骤中，算法计算每个数据点与所有质心之间的距离，并将其分配给最近的质心所代表的簇。在更新步骤中，算法计算每个簇的新质心，通常是该簇内所有点的均值。这两个步骤交替进行，直到满足停止条件。

## 2.2 K-means在图像分割中的实现
### 2.2.1 图像预处理与特征提取

图像预处理是图像分割的第一步，目的是为了减少噪声和提高图像质量，从而使得后续的特征提取和聚类操作更加有效。常见的图像预处理步骤包括图像灰度化、滤波去噪、对比度调整等。

在图像分割中，特征提取是关键步骤之一。图像特征通常包括颜色、纹理、形状等。其中，颜色直方图和颜色矩是最常用的颜色特征提取方法。通过特征提取，可以将图像数据转化为可以被K-means算法处理的向量形式。

### 2.2.2 算法参数设置与优化

在应用K-means算法进行图像分割时，需要设置的参数包括簇的数量k以及迭代的最大次数。簇的数量k可以通过多种方式确定，例如肘部法则、轮廓系数等。迭代次数的设置需要在算法的运行效率和结果准确性之间取得平衡。

优化方面，可以通过多种方式提升K-means算法的性能。例如，使用K-means++算法进行初始质心的选择可以提升聚类质量。另外，还可以结合图像的局部特征信息来指导聚类过程，以提升图像分割的准确性。

### 2.2.3 实例分析：K-means在静态图像分割中的应用

假设我们要使用K-means算法对一张静态图像进行分割。首先，我们需要将图像转换成灰度图，接着应用中值滤波去除噪声，并执行直方图均衡化增强图像对比度。然后，我们提取颜色直方图作为特征向量，并使用K-means算法进行聚类。

在Python中，我们可以使用scikit-learn库来实现K-means聚类。以下是一个简单的代码示例：

from sklearn.cluster import KMeans
from skimage.io import imread
from skimage.color import rgb2gray
import matplotlib.pyplot as plt

# 读取图像并转换为灰度图
image = rgb2gray(imread('image.jpg'))

# 提取特征（这里我们使用像素值作为特征）
pixels = image.reshape((-1, 1))

# 应用K-means算法
kmeans = KMeans(n_clusters=3)
kmeans.fit(pixels)

# 获取聚类结果并可视化
labels = kmeans.predict(pixels)
segmented_image = labels.reshape(image.shape)

plt.imshow(segmented_image, cmap='gray')
plt.show()

在执行这段代码后，我们会得到一张分割后的图像，其中不同颜色代表不同的簇。通过优化算法参数和图像预处理步骤，我们可以得到更加精确的分割效果。

## 2.3 K-means分割技术的挑战与解决
### 2.3.1 常见问题与挑战

K-means算法虽然在图像分割领域得到了广泛的应用，但它也存在一些问题和挑战。首先，K-means算法对初始质心的选择非常敏感，如果初始质心选择不当，可能导致局部最优解，从而影响聚类结果。其次，K-means算法要求提前确定簇的数量k，这在实际应用中往往是未知的，需要通过额外的方法来估算。

此外，K-means算法属于硬聚类方法，它要求每个数据点严格属于一个簇，这在处理模糊或重叠的图像区域时会遇到问题。最后，由于K-means算法的计算复杂度较高，处理大规模图像数据时可能面临性能瓶颈。

### 2.3.2 实践中的改进策略

针对K-means算法在图像分割中遇到的问题和挑战，我们可以采取一些改进策略。例如，为了缓解初始质心选择的敏感性，可以采用多次运行算法并选择最佳结果的策略。为了确定簇的数量k，可以使用一些启发式算法，如肘部法则，来辅助决策。

为了处理模糊重叠区域，可以采用软聚类方法，如模糊C均值聚类（Fuzzy C-Means，FCM），它可以允许数据点以一定的隶属度属于多个簇。性能瓶颈问题可以通过并行计算或分布式计算来解决，以提升处理大规模数据的能力。

## 2.4 本章小结

本章我们深入探讨了K-means算法在图像分割中的应用，从其原理、实现步骤，到面临的挑战与改进策略，涵盖了图像预处理、特征提取、参数设置、优化方法以及实例分析等多个方面。K-means算法因其简洁高效的特性，在图像分割领域中占有重要地位，但在实际应用中也需要根据具体问题进行调整和优化。通过本章的介绍，读者应能对K-means算法在图像分割中的应用有一个全面的了解，并能够应用于实际问题的解决中。

# 3. K-means在特征提取中的应用

## 3.1 特征提取的基本概念

### 3.1.1 特征提取的目的与意义

在机器学习和数据挖掘领域，特征提取是一个关键步骤，旨在从原始数据中识别和构造出一组有意义的特征，这些特征能够代表数据的主要信息，同时减少数据的复杂性。特征提取的目的在于提高数据处理的效率、简化模型的复杂度以及增强模型的泛化能力。

特征提取的意义可以从以下几个方面理解：

1. **降维**：原始数据往往维度很高，高维数据不仅计算量大，而且可能包含冗余信息或噪声，通过特征提取，可以减少数据的维度，从而提高计算效率。

2. **信息保留**：一个良好的特征提取方法能够在减少维度的同时尽可能保留原始数据中的重要信息。

3. **避免过拟合**：减少特征数量能够减少模型复杂度，从而降低模型过拟合的风险。

4. **提高模型性能**：合适的特征提取可以提升模型的预测准确率和效率。

### 3.1.2 特征提取的方法概述

特征提取的方法多种多样，可以大致分为以下几类：

1. **线性方法**：如主成分分析（PCA）、线性判别分析（LDA）等，通过数学变换将数据映射到新的坐标系。

2. **基于模型的方法**：如独立成分分析（ICA）、因子分析（FA）等，这些方法建立在数据的统计模型之上。

3. **非线性方法**：如核主成分分析（KPCA）、局部线性嵌入（LLE）等，旨在探索数据的非线性结构。

4. **基于聚类的方法**：例如K-means，通过将数据集分成多个簇来发现数据中的自然分组。

在本章节中，我们将深入探讨K-means这一聚类算法在特征提取中的应用，分析其在实际问题中的表现和优势。

## 3.2 K-means算法在特征提取中的实施

### 3.2.1 算法与特征空间映射

K-means是一种迭代算法，用于将具有n个样本的数据集划分为k个簇。在特