Python动态规划算法精解：理解动态规划的思想并掌握经典算法

# 1. 动态规划算法概述**

### 1.1 动态规划的概念和特点

动态规划是一种用于解决复杂问题的算法范式，它将问题分解为一系列较小的子问题，并通过逐步解决这些子问题来求解原始问题。其特点包括：

- **子问题重叠：**子问题之间存在重叠，即相同的子问题会被重复求解。
- **最优子结构：**原始问题的最优解包含其子问题的最优解。
- **自底向上或自顶向下求解：**可以从问题底部开始逐步解决子问题，或从问题顶部开始逐步分解子问题。

# 2. 动态规划算法基本思想

动态规划算法是一种自顶向下或自底向上求解复杂问题的算法，其基本思想是将问题分解成更小的子问题，并存储这些子问题的解决方案，以避免重复计算。

### 2.1 分解子问题

动态规划算法的第一步是将复杂问题分解成更小的子问题。这些子问题应该具有以下特点：

* **独立性：**子问题之间相互独立，可以单独求解。
* **重叠性：**子问题之间存在重叠，即同一个子问题可能被多次求解。

### 2.2 存储重叠子问题

为了避免重复计算重叠的子问题，动态规划算法使用一个数据结构来存储这些子问题的解决方案。这个数据结构可以是一个数组、哈希表或其他适合存储子问题解决方案的数据结构。

### 2.3 自底向上或自顶向下求解

动态规划算法有两种求解方式：

* **自底向上：**从最小的子问题开始，逐步求解更大的子问题，直到求解出整个问题。
* **自顶向下：**从整个问题开始，逐步分解成更小的子问题，直到求解出最小的子问题，然后逐步向上求解更大的子问题。

#### 自底向上求解示例

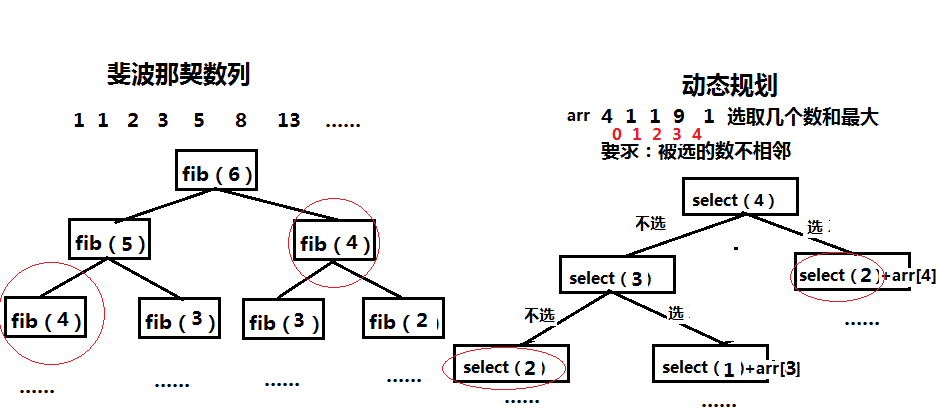
**问题：**计算斐波那契数列的第 n 项。

**子问题：**计算斐波那契数列的第 k 项（k < n）。

**存储：**使用一个数组 f 来存储斐波那契数列的第 0 项到第 n 项的值。

**求解：**

def fib(n):
    f = [0, 1]  # 初始化前两项
    for i in range(2, n + 1):
        f.append(f[i - 1] + f[i - 2])  # 求解第 i 项
    return f[n]

**代码逻辑分析：**

* 初始化数组 f，存储前两项。
* 从第 2 项开始，逐项求解斐波那契数列的每一项，并存储在数组 f 中。
* 返回数组 f 中第 n 项的值，即斐波那契数列的第 n 项。

#### 自顶向下求解示例

**问题：**计算最长公共子序列的长度。

**子问题：**计算字符串 s 和 t 的子字符串 x 和 y 的最长公共子序列的长度。

**存储：**使用一个二维数组 dp 来存储子字符串 x 和 y 的最长公共子序列的长度。

**求解：**

def lcs(s, t):
    m, n = len(s), len(t)
    dp = [[0] * (n + 1) for _ in range(m + 1)]  # 初始化二维数组

    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if s[i - 1] == t[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1  # 字符相等，最长公共子序列长度加 1
            else