Python图算法详解：图的表示、遍历和最短路径算法

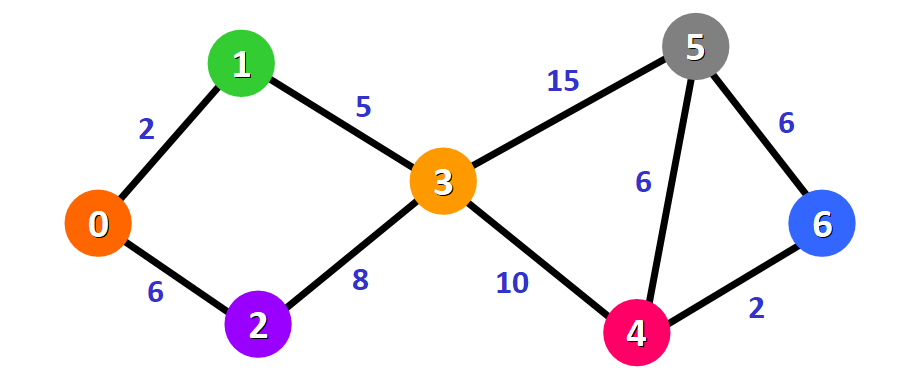
# 1. 图的基本概念和表示

图是一种数据结构，用于表示对象之间的关系。它由一组顶点和一组边组成，其中边连接顶点。图可以用来表示各种各样的问题，如社交网络、交通网络和计算机网络。

图有两种基本表示方式：邻接矩阵和邻接表。邻接矩阵是一个二维数组，其中元素表示顶点之间的权重。邻接表是一个列表，其中每个元素表示一个顶点，以及与该顶点相邻的顶点的列表。

在Python中，可以使用NetworkX库来表示图。NetworkX提供了一个Graph类，它可以用来创建和操作图。Graph类具有各种方法，用于添加和删除顶点和边，以及遍历图。

# 2. 图的遍历

图的遍历是访问图中所有顶点和边的过程。图的遍历算法有很多种，其中最常用的两种是深度优先遍历（DFS）和广度优先遍历（BFS）。

### 2.1 深度优先遍历

深度优先遍历（DFS）是一种从根节点开始，沿着一条路径一直向下探索，直到无法再向下探索为止，然后再回溯到上一个未访问的节点，继续向下探索的遍历算法。

#### 2.1.1 递归实现

使用递归可以很方便地实现深度优先遍历。递归函数的定义如下：

def dfs(graph, start):
    visited.add(start)
    print(start)
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs(graph, neighbor)

其中，`graph` 是图的邻接表表示，`start` 是起始节点，`visited` 是已访问节点的集合。

**代码逻辑分析：**

1. 将起始节点添加到已访问节点集合中。
2. 打印起始节点。
3. 遍历起始节点的所有邻居。
4. 如果邻居未被访问过，则递归调用 `dfs` 函数，以邻居为起始节点继续遍历。

**参数说明：**

* `graph`: 图的邻接表表示。
* `start`: 起始节点。

#### 2.1.2 栈实现

使用栈也可以实现深度优先遍历。栈的实现如下：

def dfs(graph, start):
    stack = [start]
    visited = set()

    while stack:
        current = stack.pop()
        if current not in visited:
            visited.add(current)
            print(current)
            for neighbor in graph[current]:
                if neighbor not in visited:
                    stack.append(neighbor)

**代码逻辑分析：**

1. 将起始节点压入栈中。
2. 只要栈不为空，就弹出栈顶元素。
3. 如果栈顶元素未被访问过，则将其添加到已访问节点集合中并打印。
4. 遍历栈顶元素的所有邻居。
5. 如果邻居未被访问过，则将其压入栈中。

**参数说明：**

* `graph`: 图的邻接表表示。
* `start`: 起始节点。

### 2.2 广度优先遍历

广度优先遍历（BFS）是一种从根节点开始，先访问根节点的所有邻居，然后再访问邻居的邻居，以此类推，直到访问完所有节点的遍历算法。

#### 2.2.1 队列实现

使用队列可以很方便地实现广度优先遍历。队列的实现如下：

def bfs(graph, start):
    queue = [start]
    visited = set()

    while queue:
        current = queue.pop(0)
        if current not in visited:
            visited.add(current)
            print(current)
            for neighbor in graph[current]:
                if neighbor not in visited:
                    queue.append(neighbor)

**代码逻辑分析：**

1. 将起始节点加入队列中。
2. 只要队列不为空，就弹出队列首元素。
3. 如果队列首元素未被访问过，则将其添加到已访问节点集合中并打印。
4. 遍历队列首元素的所有邻居。
5. 如果邻居未被访问过，则将其加入队列中。

**参数说明：**

* `graph`: 图的邻接表表示。
* `start`: 起始节点。

#### 2.2.2 层次遍历

广度优先遍历的一种特殊情况是层次遍历，即在每一层先访问所有节点，然后再访问下一层。层次遍历的实现如下：

def bfs_level(graph, start):
    queue = [(start, 0)]
    visited = set()
    levels = {}

    while queue:
        current, level = queue.pop(0)
        if current not in visited:
            visited.add(current)
            print(current)
            levels[level] = levels.get(level, []) + [current]
            for neighbor in graph[current]:
                if neighbor not in visited:
                    queue.append((neighbor, level + 1))

    return levels

**代码逻辑分析：**

1. 将起始节点和层级 0 加入队列中。
2. 只要队列不为空，就弹出队列首元素。
3. 如果队列首元素未被访问过，则将其添加到已访问节点集合中并打印。
4. 将队列首元素的层级添加到层级字典中。
5. 遍历队列首元素的所有邻居。
6. 如果邻居未被访问过，则将其和下一层级加入队列中。

**参数说明：**

* `graph`: 图的邻接表表示。
* `start`: 起始节点。

**返回：**

* `levels