【动态规划：从理论到应用】：LINGO中的优化之旅


# 摘要
本文旨在介绍动态规划算法的理论基础、软件实现及实际应用。首先，概述了动态规划的基本概念、与递归的关系以及核心要素，包括状态定义、转移方程、边界条件和初始条件。接着，探讨了动态规划的优化策略，重点分析了重叠子问题和最优子结构，以及动态规划在时间和空间复杂度方面的优化。本文还介绍了LINGO软件环境，涵盖了其基本功能、在优化问题中的应用以及高级功能的介绍。进一步地，本文演示了如何在LINGO中实现动态规划模型，并提供了经典问题的案例分析。最后，文章展望了动态规划的未来研究方向，包括其变种、扩展以及在大规模问题和与其他算法融合方面的挑战。

# 关键字
动态规划；优化策略；LINGO软件；状态转移；重叠子问题；资源分配问题

参考资源链接：[使用LINGO解决动态规划优化问题](https://wenku.csdn.net/doc/6412b4a4be7fbd1778d404dd?spm=1055.2635.3001.10343)
# 1. 动态规划简介

动态规划是一种用来解决多阶段决策问题的数学方法，它通过将复杂问题分解为更简单的子问题，进而找到最优解的策略。在IT行业中，动态规划被广泛应用在算法设计、数据分析以及各类优化问题的解决方案中，特别是当问题涉及到决策序列和最优路径时。动态规划通过构建一个状态空间，包括所有可能的决策状态，并通过迭代求解每个子问题，逐步得到整个问题的最优解。在这一过程中，动态规划强调重叠子问题的解决以及最优子结构的利用，旨在减少不必要的计算，提高效率。本章将为读者提供动态规划的基本概念、理论基础和实际应用的概览。

# 2. 动态规划的理论基础

## 2.1 动态规划的基本概念

### 2.1.1 动态规划的定义和特点

动态规划是一种解决复杂问题的算法设计技术。它将问题分解为相互重叠的子问题，并存储这些子问题的解，以避免重复计算。动态规划是通过组合子问题的解来构建原问题的解，尤其适用于具有重叠子问题和最优子结构特性的问题。这个技术通常用在优化问题中，比如最短路径、最大子数组、背包问题等。

与递归相比，动态规划的一个主要优势在于减少重复计算。递归虽然直观，但由于其重复计算相同的子问题，可能在计算复杂度上是指数级的。动态规划通过存储子问题解的表格（通常是数组或者哈希表），来避免这种重复，从而大幅优化性能。动态规划的另一个特点是通常需要将问题的解空间结构化，以便于递归或迭代地解决子问题。

### 2.1.2 动态规划与递归的关系

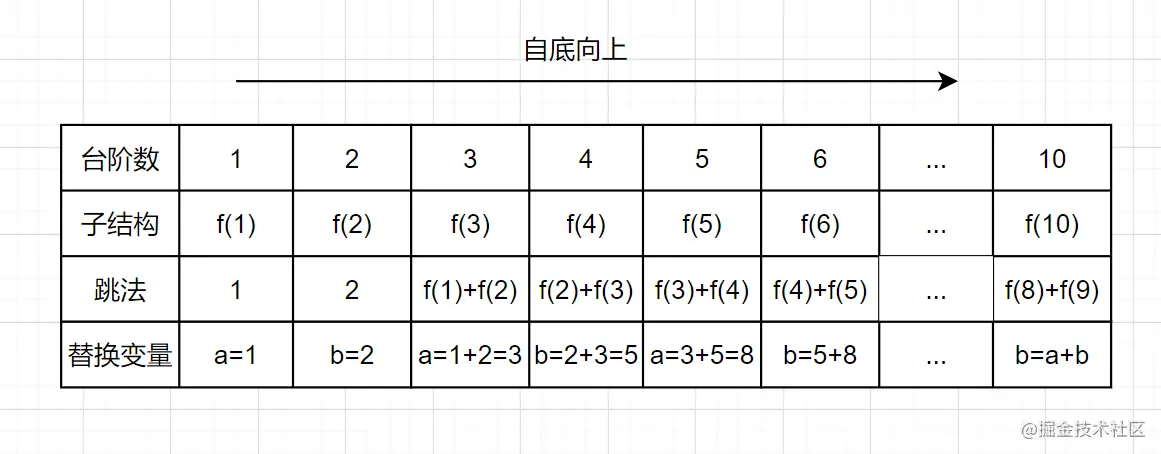
递归是动态规划中用于识别和定义子问题的一种手段。在很多情况下，我们可以用递归的形式先写出问题的直接解决方案，然后通过存储中间计算结果的方法将递归实现改为动态规划。以斐波那契数列为例，递归的实现非常直接，但效率低下，因为它涉及大量的重复计算。

在动态规划中，我们将递归方法改写为迭代形式，并引入一个表（通常是数组）来存储已经计算过的子问题的结果。这样，当遇到相同的子问题时，我们直接从表中检索结果，而不是重新计算。这种技术不仅优化了计算时间，而且使算法的空间复杂度更加合理。

## 2.2 动态规划的核心要素

### 2.2.1 状态定义和转移方程

动态规划算法的一个核心要素是状态的定义。状态通常是一个或多个变量，它们定义了子问题的空间。问题的不同阶段或选择会被映射到不同的状态。转移方程描述了从一个状态到另一个状态的变化规则。

例如，对于背包问题，状态可以定义为`dp[i][j]`，表示考虑到第`i`个物品时，对于容量为`j`的背包，所能装的最大价值。转移方程会根据是否选择当前物品（第`i`个物品），对前一个状态的值进行更新。

### 2.2.2 边界条件和初始条件

边界条件和初始条件是定义动态规划解决方案的另外两个要素。边界条件定义了问题的起点，而初始条件是算法在开始迭代之前必须设置的。在背包问题中，边界条件可能是`dp[0][j] = 0`，表示没有物品时背包的容量无论大小都为零。初始条件通常是在问题的最简单情况下解决问题的方法，比如在背包问题中，当只有一个物品时，背包容量能放下的价值就是该物品的价值。

## 2.3 动态规划的优化策略

### 2.3.1 重叠子问题和最优子结构

重叠子问题是动态规划存在的前提条件。这意味着在问题的解空间中，存在大量重复计算的子问题。在背包问题中，考虑不同组合的物品时，会重复计算相同容量的背包情况。最优子结构则是指一个问题的最优解包含了其子问题的最优解。在背包问题中，如果已知在不超过一定容量的限制下，某组物品能够达到的最大价值，那么这个信息可以用来帮助解决整个问题。

### 2.3.2 时间和空间复杂度分析

时间复杂度衡量算法执行需要的时间量，而空间复杂度衡量算法执行需要的存储空间量。动态规划通常能够将指数级的递归问题转变为多项式时间复杂度的问题。例如，原始的斐波那契数列通过递归实现的时间复杂度是指数级的，而动态规划版本的时间复杂度仅为线性。

空间复杂度的优化通常涉及到减少存储需求。在某些情况下，我们可以通过滚动数组技术减少空间需求，即只存储上一层的信息而不是所有层的信息。在背包问题中，可以仅使用一维数组来存储背包容量从`0`到`W`的最优值，而不是使用二维数组，从而将空间复杂度从`O(nW)`降低到`O(W)`，其中`n`是物品数量，`W`是背包的最大容量。

为了更好地理解动态规划的理论基础，接下来我们深入探讨动态规划的核心要素，并将理论应用于实际案例中。在下一节中，我们将结合具体的动态规划模型，分析状态定义、转移方程以及如何处理边界和初始条件。

# 3. LINGO软件环境介绍