【模拟电路测试】：PRBS应用的详尽解析与实践技巧


# 摘要
伪随机二进制序列（PRBS）在模拟电路测试中扮演着关键角色，其生成原理和数学模型为信号完整性测试和设备组件测试提供了强大的工具。本文深入探讨了PRBS的基础知识，包括其定义、特性、序列构造方法以及线性反馈移位寄存器（LFSR）的原理和实现。此外，本文还着重分析了PRBS在模拟电路测试中的实际应用，涵盖了信号完整性测试（如眼图分析和抖动测试）、设备和组件测试（如DAC和ADC测试）。测试实践技巧的章节讨论了测试设备的选择、测试环境搭建、数据捕获与分析方法，而故障诊断与排除章节则提供了常见故障模式的识别和修复策略。通过案例分析，本文展示了PRBS测试在高速串行链路和模拟信号处理器测试中的应用，提供了测试设计、实施以及优化建议。

# 关键字
PRBS；模拟电路测试；信号完整性；设备组件测试；故障诊断；案例分析

参考资源链接：[PRBS伪随机码生成原理详解及其应用](https://wenku.csdn.net/doc/64892292619bb054bf5d5634?spm=1055.2635.3001.10343)
# 1. PRBS在模拟电路测试中的作用

伪随机二进制序列（PRBS）在模拟电路测试中扮演着至关重要的角色。在高速电子通信中，PRBS作为一种有效的工具，能够模拟真实数据流量，进而检验电路在复杂信号下的性能表现。PRBS的主要作用体现在对信号完整性和电路设备性能的综合测试上，它能够提供一个可控且重复的测试环境，从而协助工程师识别和优化电路设计中的潜在问题。

在模拟电路测试中，PRBS特别适用于评估数字信号传输的性能，比如通过眼图分析来检测信号传输中的时序误差，以及通过抖动测试来评估信号同步的准确性。这种测试方法能够帮助工程师判断电路在连续运行中的可靠性和稳定性。

在下一章节中，我们将深入探讨PRBS的基本原理，包括其定义、特性以及构造方法。这将为理解PRBS如何在模拟电路测试中发挥作用打下坚实的基础。

# 2. PRBS基础知识

## 2.1 PRBS生成原理

### 2.1.1 PRBS的定义和特性

伪随机二进制序列（Pseudo-random binary sequence, PRBS）是一种看似随机但实际上是由确定性算法生成的数字序列。由于其数学上的确定性，PRBS可重复产生，常用于测试和校验电子设备性能。PRBS具有平衡的“0”和“1”的数量，具有良好的自相关特性和几乎零的互相关特性。此外，它们还拥有较长的周期，意味着序列在很长的长度上不重复。这使得PRBS成为模拟电路测试中理想的测试信号，尤其是在高速数字通信和雷达系统中。

### 2.1.2 PRBS的序列构造方法

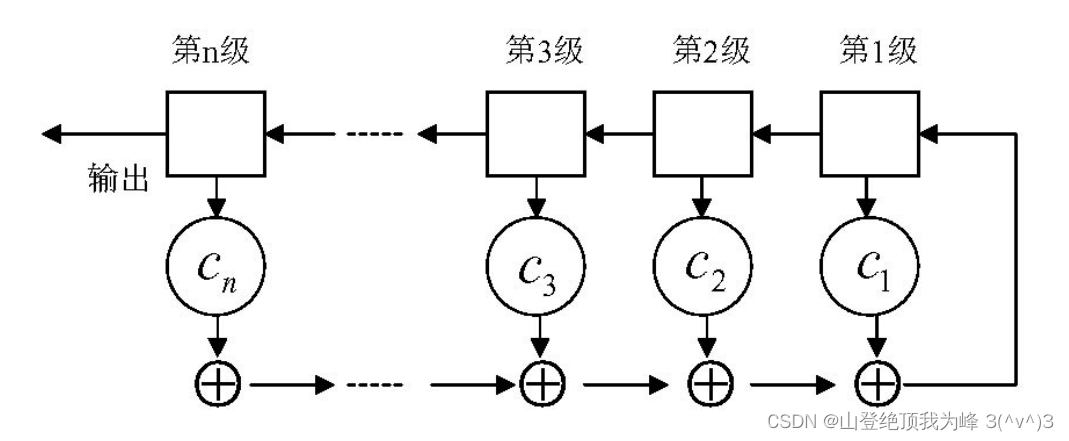
PRBS的构造基于线性反馈移位寄存器（LFSR）。一个n级的LFSR可以生成长度为\(2^n - 1\)的序列，这是一个最大长度序列（m-sequence）。序列的构造方法涉及特定的反馈抽头配置，这些配置决定了序列的周期性和其他特性。例如，一个三级LFSR（n=3），若使用反馈函数为\(f(x_3, x_2, x_1) = x_3 \oplus x_2\)，则可生成周期为\(2^3 - 1 = 7\)的PRBS序列：001110100110111…。

## 2.2 PRBS的数学模型

### 2.2.1 线性反馈移位寄存器（LFSR）的原理

LFSR是一种由若干位的移位寄存器和反馈逻辑组成的序列生成器。每个时钟周期，寄存器中的位向右移动一位，最右边的位被移出，而新加入的位是通过特定的反馈逻辑基于原寄存器内容计算得出。LFSR的反馈逻辑通常采用异或（XOR）操作实现，因为这样的操作简单且能保证生成周期性序列。反馈抽头的位置决定了序列的周期和特性，因此设计时需要根据应用需求仔细选择。

### 2.2.2 LFSR的实现与配置

实现LFSR时需要考虑几个关键因素，包括寄存器的初始状态（种子）、反馈抽头的位置以及移位的时钟频率。对于PRBS序列，LFSR的初始状态不能为全“0”，以避免生成全零序列。反馈抽头的选择是根据特定的多项式配置，这些多项式被称为m-sequence的生成多项式。例如，对于n=7的LFSR，一个常用的生成多项式是\(X^7 + X^3 + 1\)，这表示在移位寄存器的第三级和最后一级进行XOR运算。实现时，可以通过硬件逻辑电路或软件编程来配置这些参数。

### 代码示例（Python代码块）

# Python代码用于生成3级LFSR的PRBS序列
def generate_lfsr_sequence(taps, sequence_length):
    register = [1] + [0] * (len(taps) - 1)
    sequence = []
    for _ in range(sequence_length):
        sequence.append(register[-1])
        feedback = sum(register[tap] for tap in taps) % 2
        register = [feedback] + register[:-1]
    return sequence

# 配置三级LFSR的反馈抽头
taps = [2]  # 这里只用一个抽头作为例子
seq_length = 7  # 生成长度为7的序列
prbs_sequence = generate_lfsr_sequence(taps, seq_length)
print(prbs_sequence)

#### 代码逻辑分析

在上述代码块中，我们定义了一个函数`generate_lfsr_sequence`，用于生成指定长度的LFSR序列。函数接收两个参数：`taps`是一个列表，包含用于反馈的寄存器位置索引；`sequence_length`是生成序列的长度。初始时，寄存器被设置为全“0”只在最右边的位为“1”。在每个时钟周期，序列中添加了寄存器的最右边位，并根据反馈抽头位置计算新的最右边位。生成的序列是PRBS序列，按照配置的抽头和长度规则。

继续下一小节内容...

# 3. PRBS在模拟电路测试中的应用

## 3.1 信号完整性测试
### 3.1.1 PRBS在眼图分析中的应用

在高速数字通信系统中，信号完整性对于数据传输的准确性和可靠性至关重要。眼图是评估信号质量的一种常用工具，它通过重叠一系列数据位模式来展现信号的波形特征，帮助工程师观察信号在特定时间窗口内的变化情况。PRBS因其具有类似随机噪声的特性，常被用作信号传输的测试图案。

使用PRBS生成特定长度和复杂度的随机序列，然后将这些序列发送通过待测链路。捕获链路输出的信号后，将其与原始的PRBS进行比较。在眼图分析中，理想的波形是开得尽可能大且对称的眼型，其中“眼”的开合程度直接关联到信号的信噪比，而“眼”的对称性则暗示了时钟偏移的大小。通过眼图，可以直观地发现信号的抖动和失真等问题。

为了提高眼图的质量和分析的准确性，通常需要对PRBS序列进行特定的配置。例如，在生成PRBS序列时，可以调节序列的长度来模拟不同的数据传输情况。此外，通过改变信号的发送频率和幅度，可以评估接收端对不同信号条件的响应能力。

###