模糊逻辑系统预测建模优势：应对复杂系统的不确定性

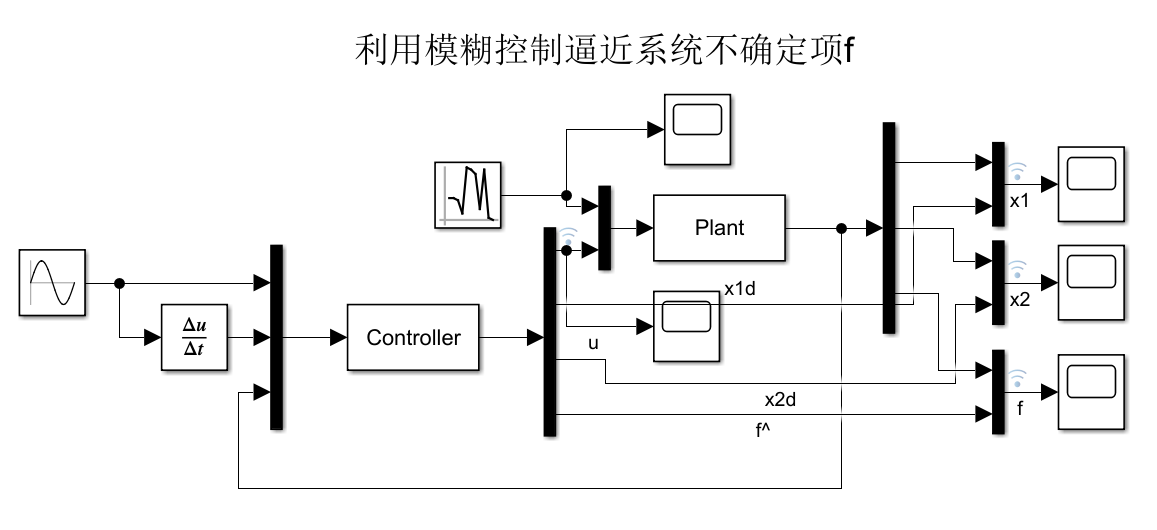
# 1. 模糊逻辑系统概述**

模糊逻辑系统是一种基于模糊理论的建模和推理方法，它允许在不确定性和模糊性条件下进行决策和预测。模糊逻辑系统通过将模糊变量和模糊规则结合起来，能够处理复杂且不精确的信息，从而做出更符合实际情况的预测。

模糊逻辑系统的主要组成部分包括模糊化、模糊推理和去模糊化。模糊化将输入变量转换为模糊集合，模糊推理根据模糊规则进行推理，去模糊化将推理结果转换为清晰值。通过这种方式，模糊逻辑系统可以处理不确定性和模糊性，并做出可靠的预测。

# 2.1 模糊逻辑的基本原理

模糊逻辑是一种基于模糊集合理论的推理方法，它允许在不确定和模糊的环境中进行推理。它将传统逻辑中的二值真值（真或假）扩展到[0, 1]范围内的连续值，以表示不确定性。

### 模糊集合

模糊集合是模糊逻辑的基础，它允许对象同时属于多个集合。与经典集合不同，模糊集合的成员资格函数是一个[0, 1]范围内的函数，表示对象属于该集合的程度。

例如，考虑一个描述温度的模糊集合“热”。对于一个给定的温度值，它可以具有0到1之间的成员资格值，其中0表示完全不热，1表示完全热。

### 模糊运算符

模糊逻辑使用一组模糊运算符来组合模糊集合。这些运算符包括：

- **交集 (AND)**：计算两个模糊集合交集的成员资格函数。
- **并集 (OR)**：计算两个模糊集合并集的成员资格函数。
- **补集 (NOT)**：计算一个模糊集合补集的成员资格函数。

### 模糊推理

模糊推理是使用模糊规则进行推理的过程。模糊规则具有以下形式：

如果 前提1 和 前提2 ... 那么 结果

其中，前提和结果都是模糊集合。模糊推理引擎使用模糊运算符来计算结果模糊集合的成员资格函数。

### 模糊逻辑的优点

模糊逻辑的主要优点包括：

- **处理不确定性**：模糊逻辑可以处理不确定和模糊的信息，使其能够在不精确或不完整的数据上进行推理。
- **人类可解释性**：模糊规则易于理解和解释，使其成为人类决策者的理想工具。
- **鲁棒性**：模糊逻辑模型对噪声和异常值具有鲁棒性，使其能够在现实世界应用中有效工作。

# 3. 模糊逻辑系统预测建模的实践应用

### 3.1 复杂系统建模中的应用

模糊逻辑系统在复杂系统建模中发挥着至关重要的作用，特别是在系统行为具有高度不确定性和非线性特征的情况下。通过将模糊逻辑的模糊推理机制引入系统建模，可以有效处理系统中存在的模糊性、不确定性和非线性关系。

**应用场景：**

* **经济预测：**预测经济指标的变化趋势，如GDP、通货膨胀率等，受多种复杂因素影响，具有高度不确定性。模糊逻辑系统可以将这些因素的模糊关系和不确定性纳入模型中，提高预测精度。
* **天气预报：**天气系统受多种因素影响，具有高度复杂性和不确定性。模糊逻辑系统可以将气象数据、历史规律和专家知识等信息融合起来，建立模糊预测模型，提高天气预报的准确性。

### 3.2 预测不确定性中的应用

模糊逻辑系统在预测不确定性中有着独特的优势。它可以处理模糊数据、不确定信息和主观判断，从而提高预测的可靠性。

**应用场景：**

* **风险评估：**评估投资风险、项目风险等，需要考虑多种不确定因素。模糊逻辑系统可以将这些因素的模糊关系和不确定性纳入模型中，提供更全面的风险评估。
* **医疗诊断：**医疗诊断过程中，患者症状和病理表现往往具有模糊性和不确定性。模糊逻辑系统可以将患者的症状、体征和专家知识等信息融合起来，建立模糊诊断模型，提高诊断的准确性。

### 3.3 实际案例分析

**案例：基于模糊逻辑的经济增长预测**

**模型构建：**

* **输入变量：**GDP、通货膨胀率、失业率等经济指标
* **输出变量：**经济增长率
* **模糊推理机制：**Mamdani推理方法
* **模糊规则：**根据经济学专家知识和历史数据建立模糊规则库

**模型评估：**

* **数据：**使用过去10年的经济数据
* **评价指标：**平均绝对误差（MAE）、均方根误差（RMSE）
* **结果：**模糊逻辑预测模型的MAE和RMSE均优于传统预测模型，表明其具有更高的预测精度

**应用价值：**

* 提高经济增长预测的准确性，为政府决策提供科学依据
* 帮助企业制定更有效的投资策略
* 促进经济的稳定发展

# 4. 模糊逻辑系统预测建模的优化

### 4.1 模型参数优化

模糊逻辑系统预测模型的参数优化至关重要，因为它直接影响模型的预测精度和泛化能力。常用的参数优化方法包括：

- **梯度下降法：**一种迭代算法，通过计算梯度并沿着负梯度方向更新参数，逐步逼近最优解。

import numpy as np

def gradient_descent(model, X, y, learning_rate=0.01, max_iter=1000):
    """梯度下降法优化模糊逻辑系统模型参数

    参数：
        model: 模糊逻辑系统模型
        X: 输入数据
        y: 输出数据
        learning_rate: 学习率
        max_iter: 最大迭代次数

    返回：
        优化后的模型参数
    """
    params = model.get_params()
    for i in range(max_iter):
        # 计算梯度
        grads = model.compute_gradients(X, y, params)

        # 更新参数
        params -= learning_rate * grads

        # 更新模型参数
        model.set_params(params)

    return params

- **粒子群优化算法：**一种基于群体智能的优化算法，模拟粒子