FreeFEM自适应网格细化：原理与实操一步到位


# 摘要
FreeFEM是一种流行的偏微分方程数值解软件，其自适应网格细化功能在提高计算精度和效率方面发挥着重要作用。本文首先概述了自适应网格细化的基本概念，随后详细介绍了其理论基础，包括数学模型、应用场景、关键技术和收敛性分析。接着，本文指导了FreeFEM软件的安装与配置流程，确保用户能够顺利搭建起计算环境。通过实践章节，本文进一步阐述了如何在FreeFEM中编写脚本和实现网格细化，同时提供了案例分析以展示自适应网格细化在不同领域的应用。最后，本文探讨了网格优化技巧和未来发展趋势，为研究者和工程师在网格细化领域提供深入见解。

# 关键字
FreeFEM；自适应网格细化；数学模型；收敛性分析；软件安装；并行计算

参考资源链接：[Freefem教程：安装、用法与高级特性（第三版）](https://wenku.csdn.net/doc/6pyzww2uzd?spm=1055.2635.3001.10343)
# 1. FreeFEM自适应网格细化概述

在数值分析领域中，自适应网格细化技术是一种提高计算精度与效率的有效方法。FreeFEM是一个使用高级语言编写的免费有限元计算软件，它能够处理自适应网格细化并解决各种偏微分方程问题。通过动态地调整网格的密度，FreeFEM能够对解的误差进行估计，并依据误差估计来优化网格分布，从而在保证数值解精度的同时，减少计算资源的使用。

自适应网格细化技术的核心在于其能够根据实际物理问题的特性，自动调整网格的尺寸和密度。在处理复杂的几何形状或者变化剧烈的物理场时，传统的均匀网格划分可能无法兼顾计算的精度与效率。而FreeFEM的自适应网格细化能力，使得我们可以更精细地捕捉到解的变化，尤其在关键区域或者梯度较大的地方能够提供更多的计算节点，从而获得更准确的数值结果。

本章节将为读者概述自适应网格细化在FreeFEM中的基本概念和应用价值，并为后续章节中关于理论基础、软件使用、实践操作以及案例分析等内容奠定基础。随着章节的深入，我们将详细探讨自适应网格细化的实现原理和操作步骤，带领读者一步步掌握这项技术，提升数值模拟的精确性和效率。

# 2. 网格细化的理论基础

## 2.1 自适应网格细化的基本原理

### 2.1.1 网格细化的数学模型

自适应网格细化（Adaptive Mesh Refinement，AMR）是一种用于数值分析的技术，它通过在模型的关键区域使用更密集的网格来提高计算精度，同时在其他区域使用较少的网格以节省计算资源。数学上，AMR涉及到有限元方法（Finite Element Method, FEM）或有限差分方法（Finite Difference Method, FDM）的网格划分技术，这些方法在空间离散化过程中生成网格结构。

在自适应网格细化中，通常使用一系列嵌套网格来覆盖感兴趣的区域。每个网格由节点和单元组成。节点是网格的顶点，单元是节点之间的连接组合，可以是三角形、四边形、四面体等。网格细化的数学模型可以用来解决偏微分方程（Partial Differential Equations, PDEs），这些方程描述了物理现象的连续性质。

在定义数学模型时，关键的步骤包括：
- 空间区域的定义：确定需要分析的物理区域。
- 网格生成：根据物理区域的复杂性自动或半自动地生成网格。
- 网格加密：在关键区域，例如梯度变化较大的地方，进行网格加密。
- 网格简化：在模型的变化较为平缓的区域，简化网格密度以减少计算量。
- 数值方法的选择：选择适当的数值方法来近似PDEs。
- 计算误差估计：基于数值解，估计解的误差。
- 网格调整：根据误差估计的结果调整网格的粗细，以实现局部精度的提高。

### 2.1.2 网格细化的目的和应用场景

网格细化的主要目的是优化数值模拟的计算效率和结果的准确性。在有限计算资源的约束下，通过在模型的关键部位使用高密度网格，提高数值求解的精度；同时在对结果影响不大的区域使用低密度网格，以节省计算资源和时间。这种策略特别适用于复杂几何形状和边界条件的问题，可以有效地捕捉到物理现象的关键特征。

网格细化技术广泛应用于许多领域，包括但不限于：

- 流体力学：如计算流体动力学（Computational Fluid Dynamics, CFD）中，AMR可以用于模拟边界层流动、涡流形成、喷嘴流动等。
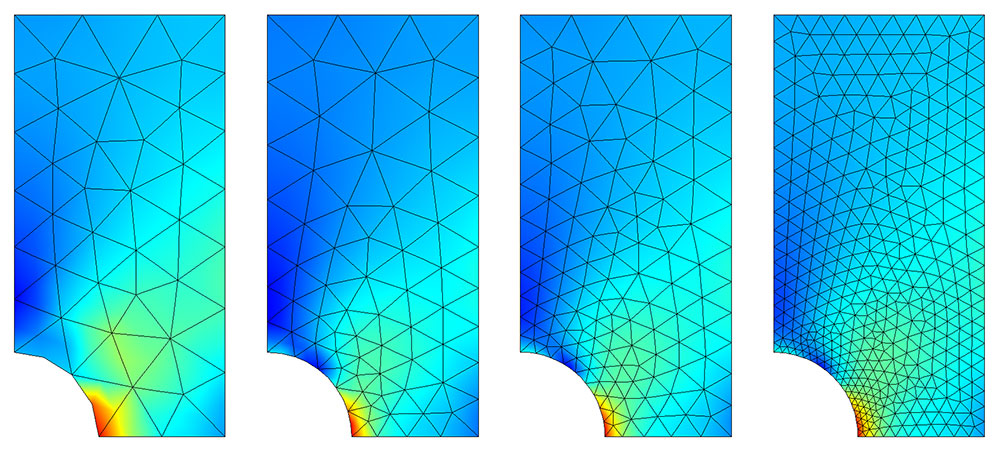
- 结构分析：在结构力学中，自适应网格细化用于详细分析应力集中的区域，如裂纹尖端、孔洞周围的应力分布。
- 地质和地球物理学：用于模拟地壳运动、地震波传播、地下水流动等问题。
- 生物医学工程：在组织和器官的模拟中，AMR可以用于精确模拟不同组织的物理特性。
- 多物理场耦合问题：在需要同时考虑流体、热、电磁和结构等多种物理场相互作用的复杂问题中，AMR提供了精确模拟的可能性。

## 2.2 网格细化的关键技术

### 2.2.1 网格生成算法

网格生成是网格细化的基础，它涉及到从连续的几何形状到离散网格节点和单元的转换。网格生成算法根据其生成方式可以分为结构化网格、非结构化网格以及多块网格算法等。

结构化网格（Structured Mesh）是规则且有规律的，通常用于形状规则的区域，如矩形、圆柱体等。在结构化网格中，节点和单元的位置和连接是预先定义的，生成过程相对简单。

非结构化网格（Unstructured Mesh）则适用于复杂几何区域，如复杂的流体动力学问题。非结构化网格可以是三角形、四边形、四面体、六面体等，节点的连接顺序并不固定，能更灵活地适应复杂的边界条件。

多块网格（Multiblock Mesh）是一种折衷方案，它将整个计算区域分割成若干个块，每个块内使用结构化网格，而块与块之间通过适当的接口连接。

### 2.2.2 错误估计和网格控制策略

在自适应网格细化过程中，错误估计是至关重要的。它负责评估数值解的误差并指导网格的动态调整。错误估计可以是局部的，也可以是全局的。局部误差估计关注于单个单元或节点的误差，而全局误差估计则关注于整个计算区域的误差分布。

网格控制策略则基于错误估计的结果来决定哪些区域需要网格细化或粗化。这涉及到以下步骤：

1. **误差估计**：计算当前网格下的数值解误差。
2. **误差分析**：识别误差高的区域，这些区域需要更多的网格点来提高精度。
3. **网格调整**：根据误差分析，重新分布网格点。
4. **求解更新**：在新的网格结构上重新求解问题。
5. **收敛性检查**：检查是否达到了预定的精度标准。

常用的误差估计方法包括：

- 解导数法：通过计算解导数来估计误差。
- 残差法：基于数值解与精确解之间差异的残差来估计误差。
- 参考解法：使用更高精度的解作为参考，以估计误差。

### 2.2.3 自适应算法的收敛性分