【算法实战】：自适应快速排序版本，手写高效代码指南

# 1. 快速排序算法基础

快速排序算法是由C. A. R. Hoare在1960年提出的一种高效的排序算法，它采用了分治法的策略来对一个数组进行排序。快速排序的基本思想是通过一个“轴点”元素将数组分为两个子数组，其中一个子数组的所有元素都不大于轴点，而另一个子数组的所有元素都不小于轴点，之后递归地对这两个子数组进行快速排序。

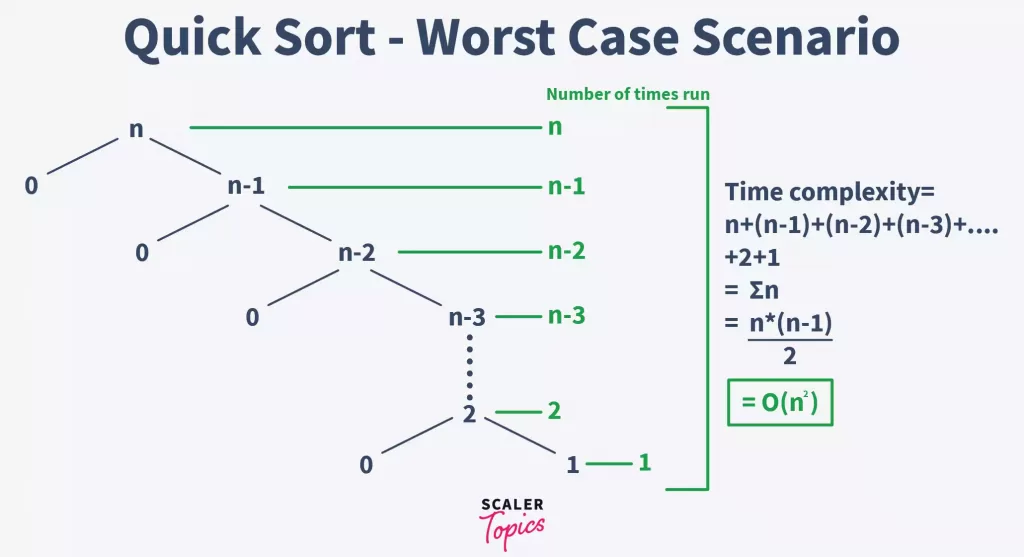
快速排序算法以其平均情况下出色的性能被广泛应用，其时间复杂度平均为O(nlogn)，空间复杂度为O(logn)，但其最坏情况下的时间复杂度为O(n^2)。这通常发生在输入数组已经是有序或者是基本有序的情况下。

快速排序可以使用递归和迭代两种方式实现，其中递归实现更加直观简单，而迭代实现则能够减少函数调用的开销。在实际应用中，可以根据具体情况选择适合的实现方式。下面我们将详细探究快速排序的理论基础和实践技巧，并提出自适应性的概念以及对算法进行优化。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

# 示例代码展示快速排序的递归实现

在上述的示例代码中，我们通过定义一个基准值（pivot），然后将数组中的元素分成小于、等于和大于基准值的三部分，最终将排序后的数组进行合并。这个递归过程不断迭代，直到数组的长度小于等于1，此时返回结果。

# 2. 自适应快速排序算法理论

### 2.1 快速排序的原理和步骤

快速排序是一种高效的排序算法，其核心在于分治法策略。其基本思想是：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

#### 2.1.1 分区操作的核心概念

分区操作是快速排序算法中最为关键的一环。它在数组中选取一个元素作为枢轴（pivot），然后重新排列数组，使得比枢轴小的元素都在枢轴的左侧，比枢轴大的元素都在枢轴的右侧。

分区操作通常由一个循环实现，该循环从数组两端开始，向中间扫描。它会持续交换左右指针指向的元素，直到它们相遇为止。此时，枢轴元素就处于其最终位置，而数组被划分为两个子数组。

def partition(array, low, high):
    pivot = array[high]  # 选择最后一个元素作为枢轴
    i = low - 1
    for j in range(low, high):
        if array[j] < pivot:
            i += 1
            array[i], array[j] = array[j], array[i]  # 交换元素
    array[i + 1], array[high] = array[high], array[i + 1]  # 将枢轴放到正确位置
    return i + 1

上述代码中，`partition` 函数执行了分区操作，返回的是枢轴最终所在的位置索引。这个位置将数组分为两部分：左侧为小于枢轴的元素，右侧为大于枢轴的元素。

#### 2.1.2 分治法策略的实现

分治法策略要求一个算法将其问题分解为若干个规模较小但类似于原问题的子问题，递归求解这些子问题，然后合并这些子问题的解成为原问题的解。

快速排序的分治法实现包含三个步骤：

1. 分区：选择一个枢轴元素并重新排列数组。
2. 递归：对枢轴左右两边的子数组进行快速排序。
3. 合并：由于分区操作已经将数组分为两部分，且这两部分已经有序，因此这里不需要额外的合并操作，递归的最后结果即为有序数组。

### 2.2 自适应性的理解

#### 2.2.1 数据特性与排序性能

快速排序的效率在很大程度上取决于枢轴元素的选择。如果每次都能选择中位数作为枢轴，则每一步划分都将数组分成两个几乎相等的部分，这样递归树的深度接近 `log(n)`，排序时间复杂度接近 `O(nlogn)`。

然而，当输入数组已经是有序或者接近有序时，快速排序的性能会显著下降，因为它会退化到 `O(n^2)` 的时间复杂度。这种情况下的快速排序就失去了自适应性。

#### 2.2.2 自适应快速排序的优化策略

自适应快速排序算法需要设计一种机制来应对各种不同的输入数据。一种常见的方法是使用“三数取中法”来选择枢轴，即取区间的首、中、尾三个位置上的元素的中位数作为枢轴。这样可以在一定程度上避免最坏情况的发生，提高算法的自适应性。

import random

def median_of_three(array, low, high):
    mid = (low + high) // 2
    if array[low] > array[mid]:
        array[low], array[mid] = array[mid], array[low]
    if array[low] > array[high]:
        array[low], array[high] = array[high], array[low]
    if array[mid] > array[high]:
        array[mid], array[high] = array[high], array[mid]
    return array[mid]

def pivot_selection(array, low, high):
    pivot = median_of_three(array, low, high)
    return pivot

上述代码通过 `median_of_three` 函数计算出三数取中的结果，然后在 `pivot_selection` 函数中返回这个中位数作为枢轴。这种方法可以在大多数情况下提高快速排序的性能，使得算法更加自适应。

### 2.3 算法的稳定性和时间复杂度

#### 2.3.1 快速排序的稳定性分析

快速排序是一种不稳定的排序算法。在排序过程中，当两个相同值的元素需要交换位置时，可能会改变它们原始的相对顺序。

一个排序算法的稳定性是指相等的元素在排序后的相对位置是否和它们排序前的相对位置相同。快速排序在处理具有相同关键字的元素时可能会破坏它们原有的顺序，因此它不是稳定的。

#### 2.3.2 时间复杂度和空间复杂度

快速排序的时间复杂度分析：

- 最好情况：`O(nlogn)`。每次分区操作都能将序列分成两个几乎相等的部分。
- 平均情况：`O(nlogn)`。即使数据不均匀分布，分区操作也会保证递归的深度大致在 `log(n)`。
- 最坏情况：`O(n^2)`。当数据完全有序或者接近有序时，分区操作产生的两个子序列高度不平衡，导致递归深度达到 `n`。

快速排序的空间复杂度分析：

快速排序是一种原地排序算法，在最好、平均和最坏情况下，其空间复杂度均为 `O(logn)`。这是因为快速排序是递归进行的，需要的额外空间主要用于递归调用的栈空间。尽管如此，使用尾递归优化可以将空间复杂度降低到 `O(1)`，但这在标准的快速排序实现中并不常见。

本章节内容深入探讨了快速排序的基本原理和步骤，同时对算法的自适应性进行了详细说明。此外，通过对稳定性、时间复杂度和空间复杂度的分析，为理解快速排序提供了全面的理论支持。在此基础上，下一章将介绍快速排序在实际应用中的技巧与优化方法。

# 3. 自适应快速排序实践技巧

## 3.1 分区方法的改进

### 3.1.1 三数取中法

三数取中法是快速排序中常用的改进技术，其基本思想是：在进行分区操作时，选取数据序列中的首、中、尾三个元素的中位数作为枢轴（pivot）。这种方法可以在一定程度上避免因最坏情况（如输入数组已经有序或基本有序）导致的快速排序退化成O(n^2)的时间复杂度。

代码块展示：

def median_of_three(data, low, high):
    mid =