滤波器在数据科学中的应用：数据清洗和特征工程，不可或缺

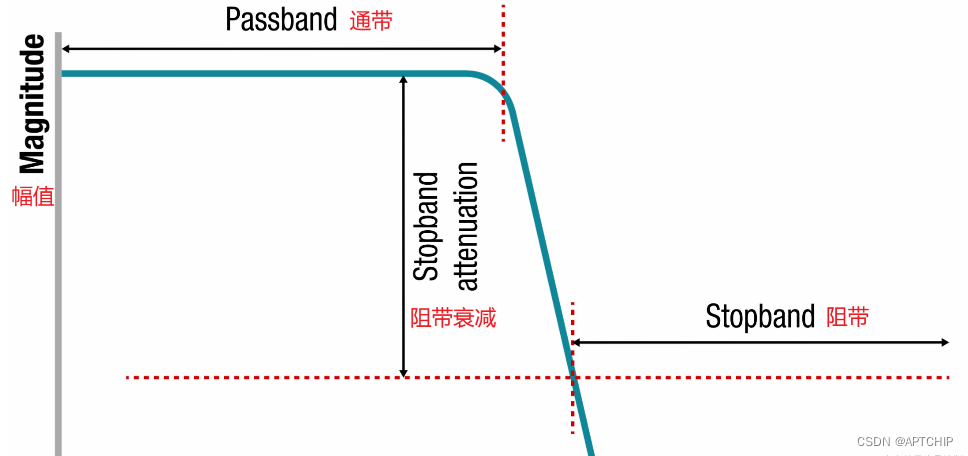
# 1. 滤波器在数据科学中的概述**

滤波器在数据科学中扮演着至关重要的角色，它可以有效地从数据中提取有价值的信息，并消除噪声和异常值。滤波器广泛应用于数据清洗、特征工程和机器学习模型训练等各个阶段。

数据科学中的滤波器主要分为两大类：**平滑滤波器**和**变异滤波器**。平滑滤波器通过平均或加权平均相邻数据点来平滑数据，从而消除噪声。变异滤波器则通过计算数据点的方差或标准差来检测异常值，并将其从数据集中移除。

# 2. 数据清洗中的滤波器应用

数据清洗是数据科学管道中至关重要的一步，它涉及到识别和处理数据中的错误、不一致和缺失值。滤波器在数据清洗中扮演着至关重要的角色，它们可以帮助识别和删除异常值，填充缺失值，从而提高数据的质量。

### 2.1 缺失值处理

缺失值是数据清洗中常见的问题，它们会影响数据的完整性和准确性。处理缺失值的方法有两种：填充和删除。

#### 2.1.1 缺失值填充

缺失值填充是指使用估计值或其他数据点来替换缺失值。常用的填充方法包括：

- **均值填充：**用该特征的平均值填充缺失值。
- **中位数填充：**用该特征的中位数填充缺失值。
- **众数填充：**用该特征中最常见的非缺失值填充缺失值。

import pandas as pd

# 创建一个包含缺失值的数据框
df = pd.DataFrame({
    'name': ['John', 'Mary', 'Bob', np.nan],
    'age': [20, 25, 30, np.nan]
})

# 使用均值填充缺失值
df['age'].fillna(df['age'].mean(), inplace=True)

# 使用中位数填充缺失值
df['age'].fillna(df['age'].median(), inplace=True)

#### 2.1.2 缺失值删除

当缺失值过多或无法准确估计时，可以考虑删除包含缺失值的记录或特征。

# 删除包含缺失值的记录
df = df.dropna()

# 删除包含缺失值的特征
df = df.drop(columns=['age'])

### 2.2 异常值检测

异常值是数据集中与其他数据点明显不同的值。它们可能由错误、传感器故障或其他原因引起。检测和处理异常值对于确保数据的可靠性和准确性至关重要。

#### 2.2.1 统计方法

统计方法是检测异常值最常用的方法。它们基于数据分布的统计特性，例如均值、标准差和四分位数。

- **Z分数：**Z分数衡量一个数据点与均值的距离。异常值通常具有较高的Z分数（大于3或小于-3）。
- **箱形图：**箱形图显示数据分布的四分位数和异常值。异常值通常位于箱形图的须须之外。

import numpy as np
import matplotlib.pyplot as plt

# 创建一个包含异常值的数据集
data = np.random.normal(100, 10, 100)
data[50] = 200

# 计算Z分数
z_scores = (data - np.mean(data)) / np.std(data)

# 绘制箱形图
plt.boxplot(data)
plt.show()

#### 2.2.2 机器学习方法

机器学习方法也可以用于检测异常值。这些方法基于数据中的模式和关系。

- **孤立森林：**孤立森林是一种无监督机器学习算法，它通过隔离与其他数据点不同的数据点来检测异常值。
- **局部异常因子（LOF）：**LOF算法计算每个数据点与周围邻居的局部密度。异常值通常具有较高的LOF分数。

from sklearn.ensemble import IsolationForest
from sklearn.neighbors import LocalOutlierFactor

# 创建一个孤立森林模型
iso_forest = IsolationForest()
iso_forest.fit(data.reshape(-1, 1))

# 预测异常值
anomalies = iso_forest.predict(data.reshape(-1, 1))

# 创建一个LOF模型
lof = LocalOutlierFactor()
lof.fit(data.reshape(-1, 1))

# 预测异常值
lof_scores = lof.score_samples(data.reshape(-1, 1))

# 3. 特征工程中的滤波器应用

特征工程是数据科学中至关重要的一步，它涉及到对原始数据进行转换和选择，以提高机器学习模型的性能。滤波器在特征工程中扮演着重要的角色，它们可以帮助我们选择最具信息量和最相关的特征，并减少特征的维度。

### 3.1 特征选择

特征选择是特征工程中最重要的任务之一。其目的是从原始特征集中选择一个最优子集，该子集包含对目标变量最具预测性的特征。有三种主要特征选择方法：

#### 3.1.1 过滤法

过滤法是一种基于特征本身统计性质的特征选择方法。它不考虑目标变量，而是根据特征的方差、信息增益或其他统计量来对特征进行评分。评分较高的特征被认为更具信息量，因此被选择。

**代码块：**

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

# 使用卡方检验选择前 10 个特征
selector = SelectKBest(chi2, k=10)
selected_features = selector.fit_transform(X, y)

**逻辑分析：**

该代码块使用卡方检验作为过滤法来选择特征。`SelectKBest` 类可以根据指定的统计量（在本例中为卡方检验）对特征进行评分，并选择评分最高的 `k` 个特征。

#### 3.1.2 包装法

包装法是一种基于机器学习模型性能的特征选择方法。它使用机器学习模型作为评估函数，迭代地添加或删除特征，直到找到一个最优子集。