MATLAB在线数值计算指南：解决科学和工程难题

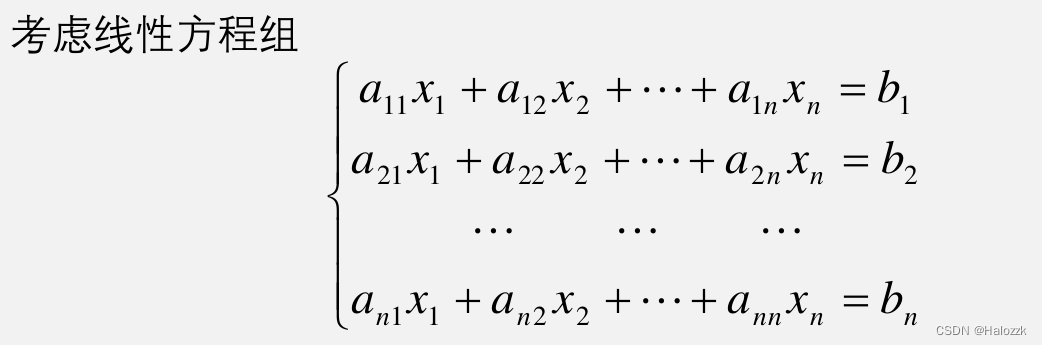
# 1. MATLAB概述

MATLAB（矩阵实验室）是一种用于科学和工程计算的高级编程语言和交互式环境。它由MathWorks公司开发，被广泛应用于各个领域，包括数学、工程、科学、金融和数据分析。

MATLAB的主要特点包括：

- **交互式环境：**MATLAB提供了一个交互式命令窗口，允许用户输入命令并立即获得结果。这使得MATLAB非常适合探索数据、开发算法和调试代码。
- **强大的数值计算能力：**MATLAB内置了丰富的数学函数库，用于执行各种数值计算，如线性代数、微积分、优化和统计分析。
- **易于使用的编程语言：**MATLAB的语法简单易懂，类似于数学符号，使其易于学习和使用。
- **丰富的工具箱：**MATLAB提供了广泛的工具箱，为特定领域提供了额外的功能，如图像处理、控制系统和数据分析。

# 2. MATLAB编程基础

### 2.1 数据类型和变量

MATLAB提供多种数据类型来表示不同类型的数据，包括：

- **数字类型：** double（双精度浮点数）、single（单精度浮点数）、int8（8位整数）、int16（16位整数）、int32（32位整数）、int64（64位整数）、uint8（8位无符号整数）、uint16（16位无符号整数）、uint32（32位无符号整数）、uint64（64位无符号整数）
- **字符类型：** char（单个字符）、string（字符串）
- **逻辑类型：** logical（布尔值）
- **单元格数组：** cell（可以存储不同类型数据的单元格数组）
- **结构体：** struct（包含具有命名字段的异构数据的结构体）

变量用于存储数据，并使用变量名对其进行引用。要创建变量，只需将值分配给变量名即可，例如：

a = 10;
b = 'Hello';
c = true;

### 2.2 运算符和表达式

MATLAB提供各种运算符和表达式来执行数学和逻辑运算。

- **算术运算符：** +（加）、-（减）、*（乘）、/（除）、^（幂）
- **关系运算符：** ==（等于）、~=（不等于）、<（小于）、>（大于）、<=（小于或等于）、>=（大于或等于）
- **逻辑运算符：** &（与）、|（或）、~（非）

表达式是运算符和操作数的组合，用于计算值。例如：

x = 2 + 3 * 4;  % x = 14
y = (a > 5) & (b == 'Hello');  % y = true

### 2.3 流程控制

流程控制语句用于控制程序的执行流程。

- **条件语句：** if-else、switch-case
- **循环语句：** for、while、do-while

条件语句根据条件执行不同的代码块。例如：

if a > 10
    disp('a is greater than 10');
else
    disp('a is not greater than 10');
end

循环语句重复执行一段代码，直到满足特定条件。例如：

for i = 1:10
    disp(i);
end

### 2.4 函数和脚本

函数是可重用的代码块，可以接受输入参数并返回输出值。脚本是包含一系列命令的文本文件，用于执行特定任务。

要创建函数，请使用以下语法：

function [output_args] = function_name(input_args)
    % 函数体
end

要创建脚本，请将命令保存在具有 `.m` 扩展名的文件中。

函数和脚本可以提高代码的可重用性和可维护性。

# 3. 数值计算**

### 3.1 线性代数

线性代数是数值计算中至关重要的一个领域，它涉及到矩阵、向量和线性方程组的运算和求解。MATLAB提供了丰富的线性代数函数，可以高效地处理各种线性代数问题。

#### 矩阵和向量操作

MATLAB使用矩阵和向量来表示数据。矩阵是一个二维数组，而向量是一个一维数组。MATLAB提供了各种矩阵和向量操作函数，包括：

- 创建矩阵和向量：`zeros()`, `ones()`, `eye()`, `rand()`
- 矩阵和向量运算：加减乘除、转置、求逆
- 矩阵分解：LU分解、QR分解、奇异值分解

#### 线性方程组求解

线性方程组求解是线性代数中的一个基本问题。MATLAB提供了多种方法来求解线性方程组，包括：

- 直接求解法：`\`, `inv()`
- 迭代求解法：`gmres()`, `bicgstab()`

#### 矩阵特征值和特征向量

矩阵的特征值和特征向量是其重要的性质。MATLAB提供了求解矩阵特征值和特征向量的函数：

- `eig()`：计算矩阵的特征值和特征向量
- `svd()`：计算矩阵的奇异值分解，其中包含了矩阵的特征值和特征向量

### 3.2 微积分

微积分是数学中另一个重要的领域，它涉及到导数、积分和微分方程的计算。MATLAB提供了丰富的微积分函数，可以高效地处理各种微积分问题。

#### 导数和积分

导