MATLAB遗传算法实战指南：从入门到精通，解锁优化难题

# 1. 遗传算法基础**

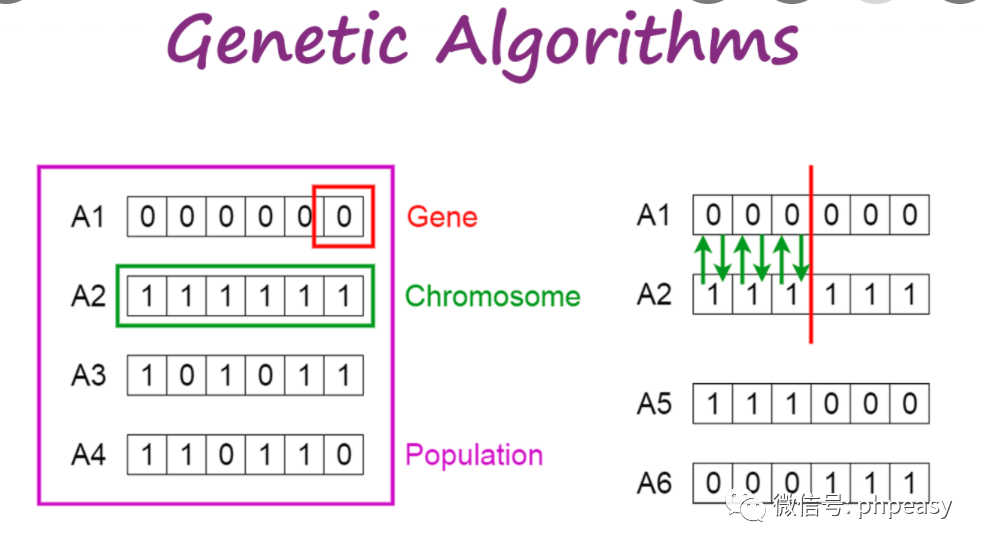
遗传算法（GA）是一种受自然进化过程启发的优化算法。它模拟了生物体的选择、交叉和变异，以找到问题的最佳解决方案。GA的基本概念包括：

- **种群：**一群候选解决方案，每个解决方案称为个体。
- **个体：**由一组基因组成的解决方案，基因决定了其特性。
- **适应度：**衡量个体优劣的函数，适应度高的个体更有可能被选择。
- **选择：**根据适应度从种群中选择个体进行繁殖。
- **交叉：**将两个个体的基因混合，产生新的个体。
- **变异：**随机修改个体的基因，引入多样性。

# 2. MATLAB中遗传算法的实现

### 2.1 MATLAB遗传算法工具箱

MATLAB提供了一个遗传算法工具箱，为用户提供了开发和实现遗传算法的便利性。该工具箱包含了一系列函数，可用于创建种群、计算适应度、执行交叉和变异操作以及管理遗传算法的迭代过程。

% 创建种群
population = gaoptimset('PopulationSize', 100);

% 计算适应度
fitness = @(x) sum(x.^2);

% 执行交叉操作
crossoverFraction = 0.8;
crossoverFunction = @crossoverArithmetic;

% 执行变异操作
mutationRate = 0.1;
mutationFunction = @mutationGaussian;

### 2.2 遗传算法参数设置

遗传算法的性能很大程度上取决于其参数设置。这些参数包括种群大小、交叉率、变异率、选择方法和终止条件。

| 参数 | 描述 |
|---|---|
| 种群大小 | 种群中个体的数量 |
| 交叉率 | 交叉操作的概率 |
| 变异率 | 变异操作的概率 |
| 选择方法 | 用于选择个体进行交叉和变异的机制 |
| 终止条件 | 算法停止的条件，例如最大迭代次数或适应度达到阈值 |

### 2.3 遗传算法流程

遗传算法的流程通常包括以下步骤：

1. **初始化种群：**随机生成一个种群，每个个体代表一个潜在的解决方案。
2. **计算适应度：**评估每个个体的适应度，适应度值越高，个体越优。
3. **选择：**根据适应度值选择个体进行交叉和变异操作。
4. **交叉：**将两个父代个体结合起来产生一个新的后代个体。
5. **变异：**对后代个体进行随机修改，引入多样性。
6. **替换：**用新产生的后代个体替换种群中的较差个体。
7. **重复步骤 2-6：**重复这些步骤，直到达到终止条件。

**流程图：**

graph LR
subgraph 遗传算法流程
    start(初始化种群) --> evaluate(计算适应度)
    evaluate --> select(选择)
    select --> crossover(交叉)
    crossover --> mutate(变异)
    mutate --> replace(替换)
    replace --> evaluate
end

# 3. 遗传算法实践应用

遗传算法是一种强大的优化算法，可用于解决各种实际问题。本章将探讨使用 MATLAB 中的遗传算法工具箱解决三个常见问题的步骤：优化函数问题、组合优化问题和图像处理问题。

### 3.1 优化函数问题

优化函数问题涉及找到一个函数的最小值或最大值。遗传算法通过模拟自然选择过程来解决此类问题。

**步骤：**

1. **定义目标函数：**确定要优化的函数。
2. **设置遗传算法参数：**指定种群大小、世代数、交叉概率和变异概率。
3. **生成初始种群：**随机生成一组候选解。
4. **评估适应度：**计算每个候选解的目标函数值。
5. **选择：**根据适应度选择最优的候选解。
6. **交叉：**通过交换基因来创建新的候选解。
7. **变异：**通过随机修改基因来引入多样性。
8. **重复步骤 4-7：**直到达到终止条件（例如，达到最大世代数）。

**示例代码：**

% 定义目标函数
f = @(x) x^2 + 10*sin(x);

% 设置遗传算法参数
options = gaoptimset('PopulationSize', 100, 'Generations', 100, 'CrossoverFraction', 0.8, 'MutationRate', 0.1);

% 生成初始种群
initialPopulation = rand(100, 1) * 10;

% 运行遗传算法
[x, fval] = ga(f, 1, [], [], [], [], [], [], [], options, initialPopulation);

% 输出结果
fprintf('最优解：%.4f\n', x);
fprintf('最优函数值：%.4f\n', fval);

**逻辑分析：**

* `gaoptimset` 函数设置遗传算法参数，包括种群大小、世代数、交叉概率和变异概率。
* `rand` 函数生成随机初始种群，范围为 0 到 10。
* `ga` 函数运行遗传算法，返回最优解和最优函数值。

### 3.2 组合优化问题

组合优化问题涉及找到一组离散变量的最佳组合，以优化目标函数。遗传算法通过模拟染色体的进化来解决此类问题。

**步骤：**

1. **编码：**将变量组合表示为染色体。
2. **设置遗传算法参数：**指定种群大小、世代数、交叉概率和变异概率。
3. **生成初始种群：**随机生成一组染色体。
4. **评估适应度：**计算每个染色体的目标函数值。
5. **选择：**根据适应度选择最优的染色体。
6. **交叉：**通过交换基因来创建新的染色体。
7. **变异：**通过随机修改基因来引入多样性。
8. **重复步骤 4-7：**直到达到终止条件。

**示例代码：**

% 定义目标函数
f = @(x) sum(x.^2);

% 设置遗传算法参数
options = gaoptimset('PopulationSize', 100, 'Generations', 100, 'CrossoverFraction', 0.8, 'MutationRate', 0.1);

% 生成初始种群
initialPopulation = randi([0, 1], 100, 10);

% 运行遗传算法
[x, fval] = ga(f, 10, [], [], [], [], [], [], [], options, initialPopulation);

% 输出结果
fprintf('最优解：\n');
disp(x);
fprintf('最优函数值：%.4f\n', fval);

**逻辑分析：**

* `randi` 函数生成随机初始种群，范围为 0 到 1。
* `ga` 函数运行遗传算法，返回最优解和最优函数值。

### 3.3 图像处理问题

遗传算法可用于解决图像处理问题，例如图像分割和特征提取。

**步骤：**

1. **图像表示：**将图像表示为像素矩阵。
2. **设置遗传算法参数：**指定种群大小、世代数、交叉概率和变异概率。
3. **生成初始种群：**随机生成一组图像分割或特征提取算法。
4. **评估适应度：**计算每个算法对图像的分割或特征提取质量。
5. **选择：**根据适应度选择最优的算法。
6. **交叉：**通过交换算法组件来创建新的算法。
7. **变异：**通过随机修改算法组件来引入多样性。
8. **重复步骤 4-7：**直到达到终止条件。

**示例代码：**

% 加载图像
image = imread('image.jpg');

% 设置遗传算法参数
options = gaoptimset('PopulationSize', 100, 'Generations', 100, 'CrossoverFraction', 0.8, 'MutationRate', 0.1);

% 生成初始种群
initialPopulation = cell(100, 1);
for i = 1:100
    initialPopulation{i} = @() kmeans(image, randi([2, 10]));
end

% 运行遗传算法
[bestAlgorithm, fval] = ga(@(x) evaluateSegmentation(x, image), 1, [], [], [], [], [], [], [], options, initialPopulation);

% 应用最优算法进行图像分割
segmentedImage = bestAlgorithm();

% 显示结果
imshow(segmentedImage);

**逻辑分析：**

* `imread` 函数加载图像。
* `gaoptimset` 函数设置遗传算法参数。
* `kmeans` 函数执行 k 均值聚类算法。
* `evaluateSegmentation` 函数评估图像分割算法的质量。
* `ga` 函数运行遗传算法，返回最优算法和最优函数值。
* `imshow` 函数显示图像分割结果。

# 4.1 适应度函数设计

适应度函数是遗传算法的核心，它衡量个体的适应性，并决定个体在种群中的存活和繁殖机会。精心设计的适应度函数对于遗传算法的成功至关重要。

### 适应度函数类型

适应度函数有多种类型，具体选择取决于优化问题的性质。常见的类型包括：

- **最小化函数：**对于最小化问题，适应度函数通常是目标函数的相反数。
- **最大化函数：**对于最大化问题，适应度函数通常是目标函数本身。
- **约束函数：**对于约束优化问题，适应度函数通常包括目标函数和约束条件的惩罚项。

### 适应度函数设计原则

设计适应度函数时，应遵循以下原则：

- **区分性：**适应度函数应能够区分不同个体的适应性，从而引导遗传算法向更优解的方向进化。
- **单调性：**对于最小化问题，适应度函数应随目标函数值增加而减小；对于最大化问题，适应度函数应随目标函数值增加而增加。
- **可比较性：**适应度函数应允许对个体进行比较和排序，以便选择最适应的个体。
- **鲁棒性：**适应度函数应对噪声和异常值具有鲁棒性，避免因个别极端值而影响遗传算法的收敛。

### 适应度函数示例

以下是一些常见的适应度函数示例：

% 最小化函数
fitness = -f(x);

% 最大化函数
fitness = f(x);

% 约束函数
fitness = f(x) - penalty * constraint(x);

其中，`f(x)`是目标函数，`constraint(x)`是约束条件，`penalty`是惩罚系数。

### 适应度函数优化

在某些情况下，可能需要优化适应度函数本身，以提高遗传算法的性能。优化方法包括：

- **自适应适应度函数：**根据种群的进化动态调整适应度函数。
- **多目标适应度函数：**对于多目标优化问题，使用多个适应度函数来评估个体的适应性。
- **惩罚项：**向适应度函数中添加惩罚项，以处理约束条件或其他优化目标。

# 5. MATLAB遗传算法案例研究

### 5.1 旅行商问题

**问题描述：**

旅行商问题是一个经典的组合优化问题，目标是在给定城市列表中找到一条最短的路径，使路径经过每个城市一次并返回起点。

**遗传算法求解：**

1. **编码：**使用整数数组表示路径，每个元素代表一个城市。
2. **适应度函数：**路径长度的倒数。
3. **交叉算子：**顺序交叉或部分匹配交叉。
4. **变异算子：**交换变异或插入变异。

**代码示例：**

% 城市坐标
cities = [1, 2; 3, 4; 5, 6; 7, 8; 9, 10];

% 遗传算法参数
populationSize = 100;
numGenerations = 100;
crossoverProbability = 0.8;
mutationProbability = 0.2;

% 创建遗传算法对象
ga = gaoptimset('PopulationSize', populationSize, ...
                'Generations', numGenerations, ...
                'CrossoverFraction', crossoverProbability, ...
                'MutationFcn', @mutationSwap);

% 求解旅行商问题
[bestPath, bestFitness] = ga(@(path) tspFitness(path, cities), ...
                            length(cities), [], [], [], [], ...
                            1:length(cities), [], [], ga);

% 打印最优路径和路径长度
disp(['最优路径：', num2str(bestPath)]);
disp(['最优路径长度：', num2str(bestFitness)]);

### 5.2 神经网络训练

**问题描述：**

神经网络训练是一个优化问题，目标是找到一组权重和偏差，使神经网络在给定数据集上的预测误差最小。

**遗传算法求解：**

1. **编码：**使用实数数组表示权重和偏差。
2. **适应度函数：**神经网络在验证集上的准确率。
3. **交叉算子：**加权平均交叉或模拟退火交叉。
4. **变异算子：**正态分布变异或高斯变异。

**代码示例：**

% 训练数据
X = [1, 2; 3, 4; 5, 6; 7, 8; 9, 10];
y = [1; 0; 1; 0; 1];

% 遗传算法参数
populationSize = 100;
numGenerations = 100;
crossoverProbability = 0.8;
mutationProbability = 0.2;

% 创建遗传算法对象
ga = gaoptimset('PopulationSize', populationSize, ...
                'Generations', numGenerations, ...
                'CrossoverFraction', crossoverProbability, ...
                'MutationFcn', @mutationGaussian);

% 求解神经网络训练问题
[bestWeights, bestFitness] = ga(@(weights) nnFitness(weights, X, y), ...
                                size(X, 2) * size(y, 2), [], [], [], [], ...
                                -inf, inf, [], ga);

% 打印最优权重和准确率
disp(['最优权重：', num2str(bestWeights)]);
disp(['最优准确率：', num2str(bestFitness)]);

### 5.3 图像分割

**问题描述：**

图像分割是一个优化问题，目标是将图像分割成不同的区域，每个区域具有相似的特征。

**遗传算法求解：**

1. **编码：**使用整数数组表示每个像素所属的区域。
2. **适应度函数：**分割图像的相似性度量，例如归一化割切距离。
3. **交叉算子：**单点交叉或多点交叉。
4. **变异算子：**随机变异或邻域变异。

**代码示例：**

% 图像
image = imread('image.jpg');

% 遗传算法参数
populationSize = 100;
numGenerations = 100;
crossoverProbability = 0.8;
mutationProbability = 0.2;

% 创建遗传算法对象
ga = gaoptimset('PopulationSize', populationSize, ...
                'Generations', numGenerations, ...
                'CrossoverFraction', crossoverProbability, ...
                'MutationFcn', @mutationRandom);

% 求解图像分割问题
[bestSegmentation, bestFitness] = ga(@(segmentation) imageSegmentationFitness(segmentation, image), ...
                                    size(image, 1) * size(image, 2), [], [], [], [], ...
                                    1:size(image, 1) * size(image, 2), [], [], ga);

% 打印最优分割和相似性度量
disp(['最优分割：', num2str(bestSegmentation)]);
disp(['最优相似性度量：', num2str(bestFitness)]);