MATLAB遗传算法分布式计算指南：扩展优化能力，应对大规模问题

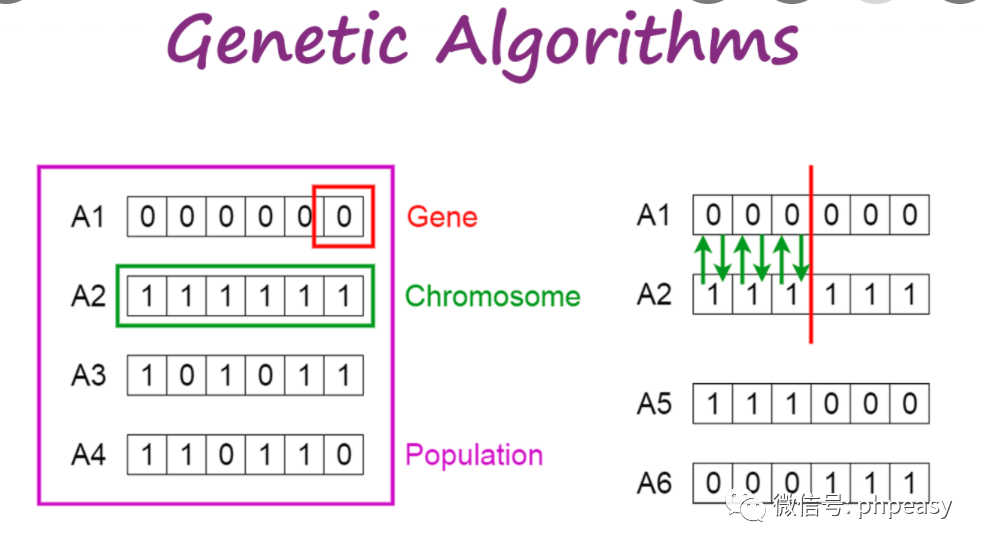
# 1. 遗传算法基础**

遗传算法（GA）是一种受生物进化过程启发的优化算法。它通过模拟自然选择、交叉和突变等机制，在搜索空间中迭代地搜索最优解。GA 的主要概念包括：

* **种群：**一组候选解，称为个体。
* **适应度：**每个个体对目标函数的评估，衡量其质量。
* **选择：**根据适应度选择个体进行繁殖。
* **交叉：**将两个个体的基因信息组合在一起，产生新的个体。
* **突变：**随机修改个体的基因信息，引入多样性。

# 2. MATLAB中的遗传算法编程

### 2.1 遗传算法的MATLAB实现

遗传算法在MATLAB中可以通过使用各种工具箱和函数来实现。最常用的工具箱是`Global Optimization Toolbox`，它提供了用于优化问题的各种算法，包括遗传算法。

要使用`Global Optimization Toolbox`中的遗传算法，可以调用`ga`函数。该函数接受以下参数：

- `fun`: 要优化的目标函数。
- `nvars`: 变量的数量。
- `lb`: 变量的下界。
- `ub`: 变量的上界。
- `options`: 遗传算法选项，包括种群大小、最大迭代次数和交叉概率。

以下代码示例演示了如何使用`ga`函数优化简单的目标函数：

% 定义目标函数
fun = @(x) x^2 + 2*x + 3;

% 设置变量边界
lb = -10;
ub = 10;

% 设置遗传算法选项
options = optimoptions('ga');
options.PopulationSize = 100;
options.MaxGenerations = 100;
options.CrossoverFraction = 0.8;

% 运行遗传算法
[x, fval] = ga(fun, 1, lb, ub, [], [], [], [], [], options);

% 输出结果
fprintf('最优解：%.4f\n', x);
fprintf('最优值：%.4f\n', fval);

**代码逻辑分析：**

1. 定义目标函数`fun`，该函数计算输入变量`x`的平方和线性组合。
2. 设置变量边界`lb`和`ub`，指定变量的取值范围。
3. 设置遗传算法选项`options`，包括种群大小、最大迭代次数和交叉概率。
4. 调用`ga`函数，传入目标函数、变量数量、变量边界和选项。
5. `ga`函数运行遗传算法，返回最优解`x`和最优值`fval`。
6. 输出最优解和最优值。

### 2.2 遗传算法参数优化

遗传算法的性能受多种参数的影响，包括种群大小、最大迭代次数、交叉概率和变异概率。这些参数需要根据具体问题进行优化，以获得最佳结果。

以下表格总结了遗传算法中常见参数及其影响：

| 参数 | 影响 |
|---|---|
| 种群大小 | 种群越大，多样性越大，但计算成本也越高 |
| 最大迭代次数 | 迭代次数越多，算法越有可能找到最优解，但计算成本也越高 |
| 交叉概率 | 交叉概率越高，种群多样性越大，但算法收敛速度越慢 |
| 变异概率 | 变异概率越高，算法探索新区域的能力越强，但算法收敛速度越慢 |

可以通过网格搜索或贝叶斯优化等技术对遗传算法参数进行优化。

### 2.3 遗传算法的并行化

遗传算法的并行化可以通过使用并行计算工具箱来实现。并行化可以显著提高遗传算法的计算速度，尤其是在处理大规模问题时。

MATLAB并行计算工具箱提供了多种并行化方法，包括：

- **并行池：**使用多个工作进程在同一台计算机上并行执行任务。
- **分布式计算：**使用多个计算机或计算节点并行执行任务。

以下代码示例演示了如何使用并行池并行化遗传算法：

% 创建并行池
parpool;

% 定义目标函数
fun = @(x) x^2 + 2*x + 3;

% 设置变量边界
lb = -10;
ub = 10;

% 设置遗传算法选项
options = optimoptions('ga');
options.PopulationSize = 100;
options.MaxGenerations = 100;
options.CrossoverFraction = 0.8;

% 运行遗传算法
[x, fval] = ga(fun, 1, lb, ub, [], [], [], [], [], options);

% 关闭并行池
delete(gc