浮点数与整数的相互转换：揭示精度损失的隐患（附案例分析）

# 1. 浮点数与整数的本质区别

浮点数和整数是计算机中表示数字的两种基本数据类型。它们在表示范围、精度和存储方式上存在本质区别。

浮点数使用科学计数法表示数字，由尾数和指数两部分组成。尾数表示数字的有效数字，指数表示数字的位数。这种表示方式使浮点数能够表示非常大或非常小的数字，但精度有限。

整数使用补码表示法表示数字，直接存储数字的二进制值。整数的表示范围有限，但精度较高，可以精确表示任何整数。

# 2. 浮点数与整数转换的理论基础

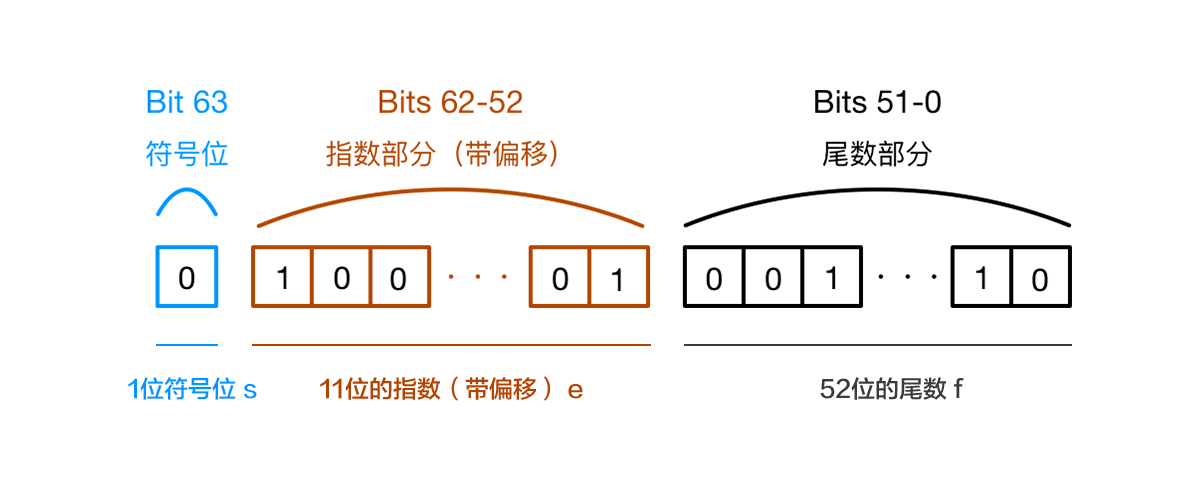
### 2.1 IEEE 754 浮点数标准

#### 2.1.1 浮点数的表示格式

IEEE 754 标准定义了浮点数的表示格式，它采用科学计数法，即：

(-1)^s * m * 2^e

其中：

* `s` 是符号位，0 表示正数，1 表示负数。
* `m` 是尾数，是一个小数。
* `e` 是指数，是一个整数。

例如，浮点数 `12.375` 可以表示为：

(-1)^0 * 1.2375 * 2^3

#### 2.1.2 浮点数的精度和范围

IEEE 754 标准定义了单精度和双精度浮点数两种格式。单精度浮点数占 32 位，双精度浮点数占 64 位。

* **单精度浮点数：**
* 尾数：23 位
* 指数：8 位
* 范围：±1.18 × 10^-38 ~ ±3.4 × 10^38
* 精度：约 7 位有效数字

* **双精度浮点数：**
* 尾数：52 位
* 指数：11 位
* 范围：±2.23 × 10^-308 ~ ±1.8 × 10^308
* 精度：约 16 位有效数字

### 2.2 整数的表示方式

#### 2.2.1 有符号整数和无符号整数

整数可以分为有符号整数和无符号整数。有符号整数使用最高位表示符号，0 表示正数，1 表示负数。无符号整数没有符号位，因此表示的范围更大。

#### 2.2.2 整数的存储和表示

整数的存储和表示方式取决于计算机的体系结构。常见的有：

* **有符号整数：**
* 补码表示法：最高位为符号位，其余位为数值位。负数使用补码表示。
* 反码表示法：最高位为符号位，其余位为数值位。负数使用反码表示。
* **无符号整数：**
* 原码表示法：所有位均表示数值。

# 3. 浮点数与整数转换的实践方法

浮点数与整数之间的转换在实际编程中十分常见，本章节将详细介绍浮点数转整数和整数转浮点数的实践方法。

### 3.1 浮点数转整数

浮点数转整数的转换方法主要有