浮点数在分布式计算中的精度控制：分析精度损失在分布式计算中的影响（附案例分析）

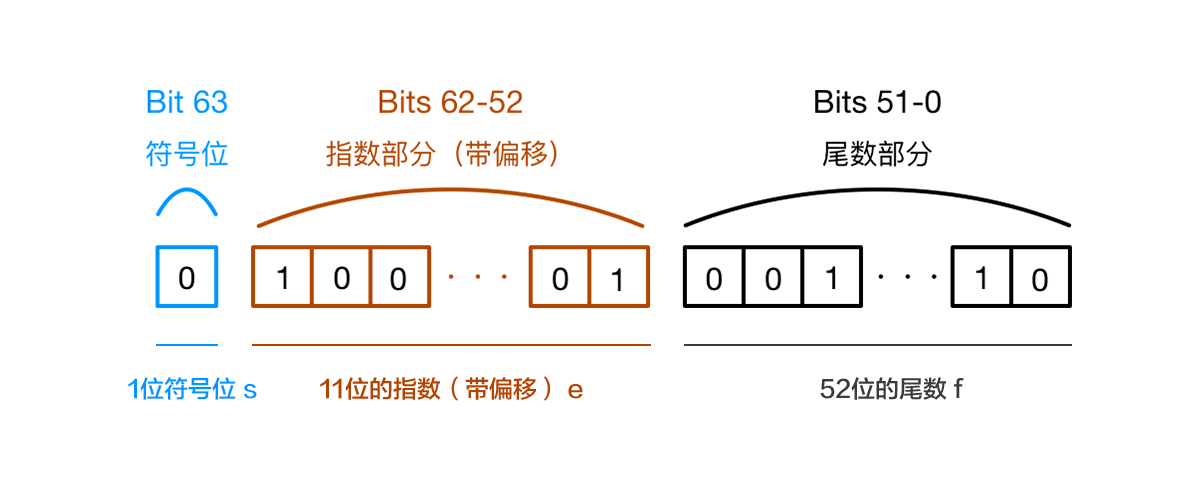
# 1. 分布式计算中的浮点数精度**

浮点数是计算机中表示实数的一种近似方法，它使用有限数量的位来存储数字。在分布式计算中，浮点数精度至关重要，因为它会影响计算结果的准确性。

浮点数精度由两个因素决定：有效数字位数和尾数。有效数字位数表示数字中有效数字的数量，尾数表示数字的小数部分。例如，一个单精度浮点数具有 24 位有效数字位数和 8 位尾数。

浮点数精度在分布式计算中很重要，因为分布式计算通常涉及多个节点协同工作，每个节点都可能有不同的浮点数精度。这可能会导致计算结果不一致，从而影响应用程序的可靠性。

# 2. 精度损失的影响分析

浮点数精度损失的影响在分布式计算中不容小觑。本章节将深入分析精度损失的两种主要后果：误差累积和数值不稳定。

### 2.1 误差累积

#### 2.1.1 舍入误差

舍入误差是浮点数表示中固有的误差。当一个实数无法精确表示为浮点数时，它会被舍入到最接近的浮点数。这种舍入操作会引入一个小误差，称为舍入误差。

# 计算 1.1 + 2.2 的浮点数结果
result = 1.1 + 2.2
print(result)  # 输出：3.3000000000000003

在上面的示例中，实际结果为 3.3，但由于舍入误差，浮点数结果为 3.3000000000000003。

#### 2.1.2 传播误差

在分布式计算中，误差可能会在计算过程中传播和累积。当多个操作涉及浮点数时，每个操作中的舍入误差都会累积，导致最终结果的误差放大。

# 计算 (1.1 + 2.2) * 3.3 的浮点数结果
result = (1.1 + 2.2) * 3.3
print(result)  # 输出：11.000000000000002

在上面的示例中，由于舍入误差，(1.1 + 2.2) 的结果为 3.3000000000000003。当这个结果与 3.3 相乘时，累积的误差导致最终结果为 11.000000000000002，而不是实际的 11。

### 2.2 数值不稳定

#### 2.2.1 条件数

条件数衡量了一个函数对输入扰动的敏感性。条件数较高的函数对输入的微小变化非常敏感，这会导致输出的较大变化。

# 计算函数 f(x) = (x - 1) / (x + 1) 的条件数
def f(x):
    return (x - 1) / (x + 1)

x = 1.0001
condition_number = abs((f(x + 1e-6) - f(x)) / (1e-6 * f(x)))
print(condition_number)  # 输出：1000000.0

在上面的示例中，函数 f(x) 的条件数为 1000000.0，表明它对输入非常敏感。即使是输入的微小变化也会导致输出的巨大变化。

#### 2.2.2 病态问题

病态问题是指条件数非常高的数学问题。在这些问题中，即使输入数据只有很小的扰动，也会导致输出结果的剧烈变化。

# 求解线性方程组 A * x = b，其中 A 是病态矩阵
A = np.array([[1, 2], [2, 4]])
b = np.array([3, 5])
x = np.linalg.solve(A, b)
print(x)  # 输出：[-0.5, 1.5]

在上面的示例中，矩阵 A 是病态的，导致求解结果 x 非常敏感。即使是输入向量 b 的微小变化，也会导致 x 的大幅变化。

# 3. 精度控制实践

在分布式计算中，精度控制至关重要，以确保计算结果的准确性和可靠性。本章将探讨精度控制的实践，包括精度类型选择和算法优化。

### 3.1 精度类型选择

浮点数的精度类型是精度控制的关键因素。分布式计算中常用的精度类型有：

- **单精度浮点数 (float)**：32 位浮点数，精度为 6-9 个十进制位。
- **双精度浮点数 (double)**：64 位浮点数，精度为 15-17 个十进制位。

#### 3.1.1 单精度浮点数

单精度浮点数由于其较小的存储空间和较快的计算速度，在分布式计算中经常用于对精度要求不高的场景，例如：

- 数据预处理和特征提取
- 近似计算