MATLAB线性插值在物理模拟中的应用：模拟流体流动、固体变形等物理现象，提升物理模拟精度

# 1. MATLAB线性插值简介

线性插值是一种在已知数据点之间估计中间值的技术。在MATLAB中，可以使用`interp1`函数进行线性插值。`interp1`函数的语法如下：

y = interp1(x, y, xi)

其中：

* `x`是已知数据点的x坐标。
* `y`是已知数据点的y坐标。
* `xi`是要估计的x坐标。

`interp1`函数将返回一个与`xi`相同长度的向量`y`，其中包含估计的y坐标值。

# 2. MATLAB线性插值在物理模拟中的理论基础

### 2.1 插值的基本原理

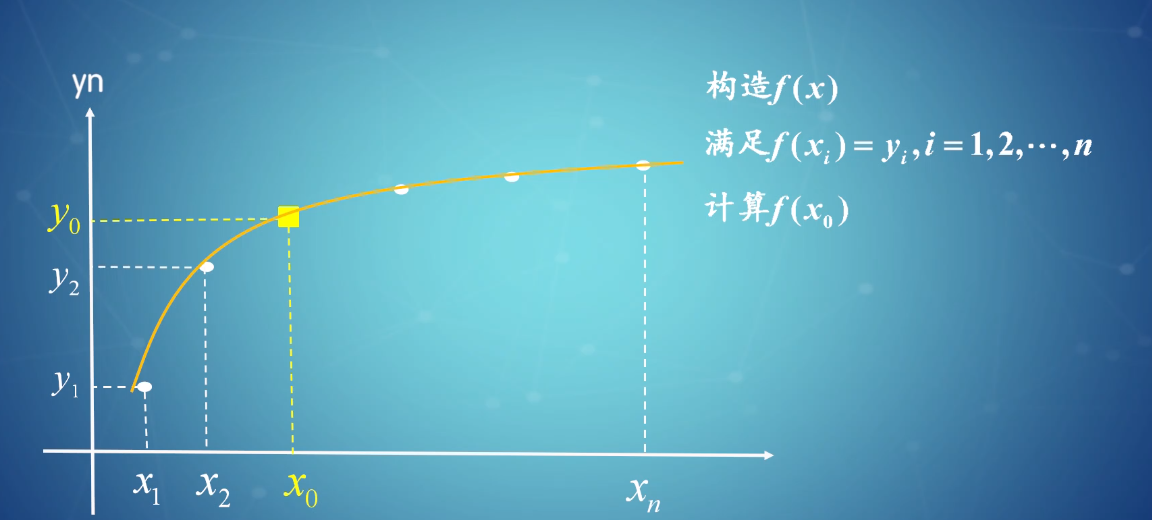
插值是一种数学技术，用于估计未知数据点之间的值。在物理模拟中，插值通常用于在已知数据点处重建连续函数。

插值的基本原理是假设未知数据点之间的函数值可以近似为已知数据点的线性组合。例如，对于两个已知数据点 (x1, y1) 和 (x2, y2)，未知数据点 x0 处的函数值 y0 可以近似为：

y0 = y1 + (y2 - y1) * (x0 - x1) / (x2 - x1)

### 2.2 线性插值的数学公式

线性插值是插值的一种特殊情况，其中未知数据点之间的函数值被近似为一条直线。线性插值的数学公式如下：

y = y0 + (y1 - y0) * (x - x0) / (x1 - x0)

其中：

* y 是未知数据点处的函数值
* y0 是已知数据点 x0 处的函数值
* y1 是已知数据点 x1 处的函数值
* x 是未知数据点
* x0 是已知数据点 x0
* x1 是已知数据点 x1

### 2.3 线性插值的误差分析

线性插值的误差是由未知数据点和已知数据点之间的函数值差异引起的。误差的大小取决于函数的非线性程度和已知数据点之间的距离。

对于非线性函数，线性插值可能会产生较大的误差。为了减少误差，可以使用更高阶的插值方法，例如二次插值或三次插值。

已知数据点之间的距离也会影响插值误差。距离越远，插值误差越大。为了减少误差，可以增加已知数据点的数量。

下表总结了线性插值的误差分析：

| 误差来源 | 误差大小 |
|---|---|
| 函数非线性程度 | 误差较大 |
| 已知数据点之间的距离 | 距离越远，误差越大 |
| 插值方法的阶数 | 阶数越高，误差越小 |

# 3.1 流体流动模拟中的应用

#### 3.1.1 流体流动方程的离散化

流体流动模拟需要求解流体流动方程，即纳维-斯托克斯方程组。该方程组是一个非线性偏微分方程组，无法直接求解。因此，需要将方程组离散化，将其转化为求解代数方程组的问题。

常用的流体流动方程离散化方法有有限差分法、有限体积法和有限元法。其中，有限差分法是最简单的方法，它将流体域离散为网格，并利用网格上的节点值来近似方程组